自动控制原理课件 (3),自动控制原理课件ppt

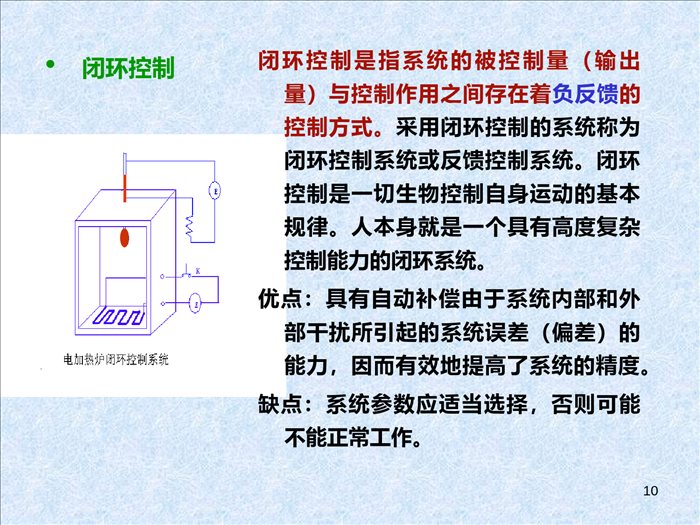
华中科技大学控制系：樊慧津自动控制原理自动控制原理(AutomaticControlTheory)(AutomaticControlTheory)学时：48+8/3.5考试：闭卷考试参考书目：1.王敏，秦肖臻编自动控制原理。北京：化学工业出版社，20032.孙德宝主编。自动控制原理。北京：化学工业出版社，20023.胡寿松主编。自动控制原理。第三版。北京：国防工业出版社，19944.王划一主编。自动控制原理。北京：国防工业出版社，2001实验安排4周（332/322），8，11周（620）南一楼0401-0402班周一（11-12）0403-0404班周四（11-12）4周（332/322），7，11周（620）南一楼0405-0406班周二（9-10）0407-0408班周二（11-12）14周计算中心四楼401机房0401-0408班周五（1-2）3主要内容绪论控制系统的数学模型线性系统的时域分析线性系统的频域分析线性系统的校正方法线性离散控制系统（采样系统分析）状态空间分析设计4第一章绪论第一章绪论1.1自动控制的基本概念：明确什么叫自动控制，正确理解被控对象、控制装置和自控系统等概念。1.2自动控制理论的发展：了解自动控制理论发展的四个主要阶段。1.3控制系统的分类：明确系统常用的分类方式，掌握各类别的含义和信息特征1.4对控制系统的基本要求：明确对自控系统的基本要求，正确理解三大性能指标的含义。5手动控制人在控制过程中起三个作用：（1）观测：用眼睛去观测温度计和转速表的指示值；（2）比较与决策：人脑把观测得到的数据与要求的数据相比较，并进行判断，根据给定的控制规律给出控制量；（3）执行：根据控制量用手具体调节，如调节阀门开度、改变触点位置。控制：操纵，节制使不超出范围或随意活动。61.11.1自动控制的基本概念自动控制的基本概念在现代科学技术的众多领域中，自动控制技术起着越来越重要的作用。如数控车床按预定程序自动切削，人造卫星准确进入预定轨道并回收等。除了在工业上广泛应用外，近几十年来，随着计算机技术的发展和应用，在宇航、机器人控制、导弹制导及核动力等高新技术领域中，自动控制技术更具特别重要的作用。不仅如此，自动控制技术的应用范围现在已扩展到生物、医学、环境、经济管理和其它许多社会生活领域中，特别在化学工业中的应用有传热设备控制，反应器控制，流体输送设备控制，精馏塔控制等。自动控制已成为现代社会生活中不可缺少的一部分。7自动控制：自动控制，就是在没有人直接参与的情况下，利用外加的设备或装置（控制装置），使机器、设备或生产过程（控制对象）的某个工作状态或参数（被控量）自动地按照预定的规律运行。自动控制系统：是指能够对被控对象的工作状态进行自动控制的系统。它是控制对象以及参与实现其被控制量自动控制的装置或元部件的组合，一般由控制装置和被控对象组成。一般包括三种机构：测量机构、比较机构、执行机构。自动控制系统的功能和组成是多种多样的，其结构有简单也有复杂。它可以只控制一个物理量，也可以控制多个物理量甚至一个企业机构的全部生产和管理过程；它可以是一个具体的工程系统，也可以是比较抽象的社会系统、生态系统或经济系统。8控制系统分析：已知系统的结构参数，分析系统的稳定性，求取系统的动态、静态性能指标，并据此评价系统的过程称为控制系统分析。控制系统设计（或综合）：根据控制对象和给定系统的性能指标，合理的确定控制装置的结构参数，称为控制系统设计。被控量：指被控对象中要求保持给定值、要按给定规律变化的物理量。被控量又称输出量、输出信号。给定值：系统输出量应达到的数值（例如与要求的炉温对应的电压）。扰动：是一种对自动控制系统输出量起反作用的信号，如电源电压的波动、环境温度的变化。9开环控制是指系统的被控制量（输出量）只受控于控制作用，而对控制作用不能反施任何影响的控制方式。采用开环控制的系统称为开环控制系统。优点：结构简单，成本低廉，易于实现缺点：对扰动没有抑制能力，控制精度低控制方式•开环控制10•闭环控制闭环控制是指系统的被控制量（输出量）与控制作用之间存在着负反馈的控制方式。采用闭环控制的系统称为闭环控制系统或反馈控制系统。闭环控制是一切生物控制自身运动的基本规律。人本身就是一个具有高度复杂控制能力的闭环系统。优点：具有自动补偿由于系统内部和外部干扰所引起的系统误差（偏差）的能力，因而有效地提高了系统的精度。缺点：系统参数应适当选择，否则可能不能正常工作。11反馈的概念反馈：把输出量送回到系统的输入端并与输入信号比较的过程。若反馈信号是与输入信号相减而使偏差值越来越小，则称为负反馈；反之，则称为正反馈。显然，负反馈控制是一个利用偏差进行控制并最后消除偏差的过程，又称偏差控制。同时，由于有反馈的存在，整个控制过程是闭合的，故也称为闭环控制。12比较以上两种控制方式由于开环控制的特点是控制装置只按照给定的输入信号对被控制量进行单向控制，而不对控制量进行测量并反向影响控制作用。这样，当炉温偏离希望值时，开关K的接通或断开时间不会相应改变。因此，开环控制不具有修正由于扰动（使被控制量偏离希望值的因素）而出现的被控制量与希望值之间偏差的能力，即抗干扰能力差。在闭环控制中，被控量一般是由测量装置检测并反馈到输入端，然后由比较装置将它与输入信号综合得到偏差（误差），有时，测量与综合作用是由一个装置完成的，如水银温度计。由于采用了接触式水银温度计，可以不断对炉温进行测量和比较，根据炉温的实际偏差进行控制，提高了控制精度和抗干扰能力。13是开环和闭环控制相结合的一种控制方式。它是在闭环控制回路的基础上，附加一个输入信号或扰动信号的顺馈通路，用来提高系统的控制精度。顺馈通路通常由对输入信号的补偿器或对扰动信号的补偿器组成。优点：具有很高的控制精度，可以抑制几乎所有的可量测扰动缺点:补偿器的参数要有较高的稳定性•复合控制14方框图的概念•方框控制装置和被控对象分别用方框表示•信号线方框的输入和输出以及它们之间的联接用带箭头的信号线表示•输入信号进入方框的信号•输出信号离开方框的信号信号线方框信号线输入信号输出信号15开环控制系统方框图控制装置被控对象输入量输出量（被控制量）输入量：加在电阻丝两端的电压被控制对象：炉子被控制量（输出量）：炉温控制装置：开关K和电热丝，对被控制量起控制作用。16温度计继电器电阻丝炉温输入量（炉温希望值）输出量（炉温实际值）扰动闭环控制的电加热炉方框图闭环控制的电加热炉方框图17人取书的控制过程眼睛脑手输入量（书的位置）输出量（手的位置）18闭环控制系统方框图19反馈控制系统方框图反馈控制系统的组成、名词术语和定义201.21.2自动控制理论的发展自动控制理论的发展自动控制理论是研究自动控制共同规律的技术科学。既是一门古老的、已臻成熟的学科，又是一门正在发展的、具有强大生命力的新兴学科。从1868年马克斯威尔（J.C.Maxwell）提出低阶系统稳定性判据至今一百多年里，自动控制理论的发展可分为四个主要阶段：第一阶段：经典控制理论（或古典控制理论）的产生、发展和成熟；第二阶段：现代控制理论的兴起和发展；第三阶段：大系统控制兴起和发展阶段；第四阶段：智能控制发展阶段。21经典控制理论控制理论的发展初期，是以反馈理论为基础的自动调节原理，主要用于工业控制。第二次世界大战期间，为了设计和制造飞机及船用自动驾驶仪、火炮定位系统、雷达跟踪系统等基于反馈原理的军用装备，进一步促进和完善了自动控制理论的发展。1868年，马克斯威尔（J.C.Maxwell）提出了低阶系统的稳定性代数判据。1875年和1896年，数学家劳斯（Routh）和赫尔威茨（Hurwitz）分别独立地提出了高阶系统的稳定性判据，即Routh和Hurwitz判据。二战期间（1938-1945年）奈奎斯特（H.Nyquist）提出了频率响应理论1948年，伊万斯（W.R.Evans）提出了根轨迹法。至此，控制理论发展的第一阶段基本完成，形成了以频率法和根轨迹法为主要方法的经典控制理论。22经典控制理论的基本特征（1）主要用于线性定常系统的研究，即用于常系数线性微分方程描述的系统的分析与综合；（2）只用于单输入，单输出的反馈控制系统；（3）只讨论系统输入与输出之间的关系，而忽视系统的内部状态，是一种对系统的外部描述方法。基本方法：根轨迹法，频率法，PID调节器（频域）反馈控制是一种最基本最重要的控制方式，引入反馈信号后，系统对来自内部和外部干扰的响应变得十分迟钝，从而提高了系统的抗干扰能力和控制精度。与此同时，反馈作用又带来了系统稳定性问题，正是这个曾一度困扰人们的系统稳定性问题激发了人们对反馈控制系统进行深入研究的热情，推动了自动控制理论的发展与完善。因此从某种意义上讲，古典控制理论是伴随着反馈控制技术的产生和发展而逐渐完善和成熟起来的。23现代控制理论经典控制理论只适用于单输入、单输出的线性定常系统，只注重系统的外部描述而忽视系统的内部状态。在实际应用中有很大局限性。随着航天事业和计算机的发展，20世纪60年代初，在经典控制理论的基础上，以线性代数理论和状态空间分析法为基础的现代控制理论迅速发展起来。1954年贝尔曼（R.Belman)提出动态规划理论1956年庞特里雅金（L.S.Pontryagin）提出极大值原理1960年卡尔曼（R.K.Kalman)提出多变量最优控制和最优滤波理论在数学工具、理论基础和研究方法上不仅能提供系统的外部信息（输出量和输入量），而且还能提供系统内部状态变量的信息。它无论对线性系统或非线性系统，定常系统或时变系统，单变量系统或多变量系统，都是一种有效的分析方法。基本方法：状态方程（时域）大系统理论20世纪70年代开始，现代控制理论继续向深度和广度发展，出现了一些新的控制方法和理论。如（1）现代频域方法以传递函数矩阵为数学模型，研究线性定常多变量系统；（2）自适应控制理论和方法以系统辨识和参数估计为基础，在实时辨识基础上在线确定最优控制规律；（3）鲁棒控制方法在保证系统稳定性和其它性能基础上，设计不变的鲁棒控制器，以处理数学模型的不确定性。25•随着控制理论应用范围的扩大，从个别小系统的控制，发展到若干个相互关联的子系统组成的大系统进行整体控制，从传统的工程控制领域推广到包括经济管理、生物工程、能源、运输、环境等大型系统以及社会科学领域。•大系统理论是过程控制与信息处理相结合的系统工程理论，具有规模庞大、结构复杂、功能综合、目标多样、因素众多等特点。它是一个多输入、多输出、多干扰、多变量的系统。大系统理论目前仍处于发展和开创性阶段。智能控制是近年来新发展起来的一种控制技术，是人工智能在控制上的应用。智能控制的概念和原理主要是针对被控对象、环境、控制目标或任务的复杂性提出来的，它的指导思想是依据人的思维方式和处理问题的技巧，解决那些目前需要人的智能才能解决的复杂的控制问题。被控对象的复杂性体现为:模型的不确定性，高度非线性，分布式的传感器和执行器，动态突变，多时间标度，复杂的信息模式，庞大的数据量，以及严格的特性指标等。智能控制是驱动智能机器自主地实现其目标的过程27智能控制是从“仿人”的概念出发的。其方法包括学习控制、模糊控制、神经元网络控制和专家控制等方法。281.31.3控制系统的分类控制系统的分类恒值系统和随动系统（按参考输入形式分类）恒值系统是指参考输入量保持常值的系统。其任务是消除或减少扰动信号对系统输出的影响，使被控制量（即系统的输出量）保持在给定或希望的数值上。随动系统是指参考输入量随时间任意变化的系统。其任务是要求输出量以一定的精度和速度跟踪参考输入量，跟踪的速度和精度是随动系统的两项主要性能指标。29线性系统和非线性系统（按照组成系统的元件特性分类）线性系统是指构成系统的所有元件都是线性元件的系统。其动态性能可用线性微分方程描述，系统满足叠加原理。非线性系统是指构成系统的元件中含有非线性元件的系统。其只能用非线性微分方程描述，不满足叠加原理。同时把可以进行线性化处理的系统或元件特性称为非本质非线性特性。反之，称之为本质非线性，它只能用非线性理论分析研究。30连续系统和离散系统（按照系统内信号的传递形式分类）连续系统是指系统内各处的信号都是以连续的模拟量传递的系统。如果系统内某处或数处信号是以脉冲序列或数码形式传递的系统则称为离散系统。其脉冲序列可由脉冲信号发生器或振荡器产生，也可用采样开关将连续信号变成脉冲序列，这类控制系统又称为采样控制系统或脉冲控制系统。而用数字计算机或数字控制器控制的系统又称为数字控制系统或计算机控制系统。311.41.4控制系统的性能指标控制系统的性能指标对控制系统性能的要求概括为三方面：稳，准，快稳定性控制系统运行的必要条件，不稳定的系统是不能工作的动态性能系统动态响应的快速性，系统的过渡过程越短越好稳态性能过渡过程结束，到达稳态后系统的控制精度的度量y(t)t0y(t)t0y(t)t0y(t)t0(a)(b)(c(d32稳定性系统在受到扰动作用后自动返回原来的平衡状态的能力。如果系统受到扰动作用（系统内或系统外）后，能自动返回到原来的平衡状态，则该系统是稳定的。稳定系统的数学特征是其输出量具有非发散性；反之，系统是不稳定系统。33动态性能当系统受到外部扰动的影响或者参考输入发生变化时，被控量会随之发生变化，经过一段时间，被控量恢复到原来的平衡状态或到达一个新的给定状态，称这一过程为过渡过程在时域中，常用单位阶跃信号作用下，系统输出的超调量p,上升时间Tr，峰值时间Tp,过渡过程时间（或调整时间）Ts和振荡次数N等特征量表示。34稳态误差指稳定系统在完成过渡过程后的稳态输出偏离希望值的程度。开环控制系统的稳态误差通常与系统的增益或放大倍数有关，而反馈控制系统（闭环系统）的控制精度主要取决于它的反馈深度。稳态误差越小，系统的精度越高，它由系统的稳态响应反映出来。35作业Page6.2,3Duedate:29thSep.周六36小结明确什么叫自动控制，正确理解被控对象、控制装置和自控系统等概念。了解自动控制理论发展的四个主要阶段。明确系统常用的分类方式，掌握各类别的含义和信息特征明确对自控系统的基本要求，正确理解三大性能指标的含义。37预备知识•复变函数：Laplace变换（拉氏变换）,Z变换•常微分方程解法：Laplace变换和反变换•电路理论•基本的电子学和力学知识第二章控制系统的数学模型第二章控制系统的数学模型2.1基本概念：数学模型及常见的系统。2.2时域模型-微分方程：微分方程的建立及线性化。2.3复域模型–传递函数：借助拉氏变换，给出系统传递函数。经典控制理论中引用最广泛的一种模型。2.4控制系统方块图：掌握方块图的建立及化简。2.5状态空间模型：控制系统的内部模型，描述了系统内部状态、系统输出与系统输入之间的关系，深入地揭示了系统的动态特性，是现代控制理论分析、设计系统的基础。掌握系统的状态变量表达式的求取及它与传递函数之间的关系。2.12.1基本概念基本概念定义：数学模型是描述系统内部物理量（或变量）之间关系的数学表达式。建立数学模型的目的•是分析和设计控制系统的首要工作（或基础工作）。•自控系统的组成可以是电气的、机械的、液压或气动的等等，然而描述这些系统发展的模型却可以是相同的。通过数学模型来研究自控系统，可以摆脱各种不同类型系统的外部特征，研究其内在的共性运动规律。建立方法•解析法（机理模型）：依据系统及元件各变量之间所遵循的物理、化学定律，列出各变量之间的数学关系式•实验法（实验建模）：对系统施加典型测试信号（脉冲、阶跃或正弦信号），记录系统的时间响应曲线或频率响应曲线，从而获得系统的传递函数或频率特性常见的控制系统常见的控制系统1、集中参数系统变量仅仅是时间的函数。这类系统建立的动态数学模型通常是微分方程。2、分布参数系统变量不仅是时间函数，而且还是空间的函数。这类系统建立的动态数学模型通常是偏微分方程。如很大的蒸馏罐，温度随空间位置不同是有梯度变化的。在实际系统中，大多数系统都是分布式参数系统，但由于偏微分方程求解比较困难，因此在一定误差允许范围内，对系统作一个近似，近似为集中参数系统，这样就可以用微分方程进行分析。413、线性系统–能够用线性数学模型(线性的代数方程、微分方程、差分方程等)描述的系统，称为线性系统。这类系统的基本特性，即输出响应特性、状态响应特性、状态转移特性等均满足线性关系。–对于控制系统而言，由线性元件构成的系统为线性系统线性系统，其运动方程一般为线性微分方程。若其各项系数为常数，则称为线性定常系线性定常系统统。–在动态研究中，如果系统在多个输入作用下的输出等于各输入单独作用下的输出和（可加性），并且当输入增大倍数时，输出相应增大同样的倍数（均匀性），就满足叠加原理，因而系统可以看成线性系统–非线性系统：描述系统的数学模型是非线性微分方程，其特性是不能应用叠加原理。424、非线性系统–不满足叠加原理的系统，就是非线性系统。因此非线性系统对两个输入量的响应不能单独进行计算，因此系统分析将比较困难，很难找到一般通用方法。但在实际系统中，绝对线性的系统是不存在的，通常所谓的线性系统也是在一定的工作范围内才保证线性的，如放大器，在小信号时可能出现“死区”，在大信号时，又可能出现饱和现象，如图所示即为几种常见的非线性的关系曲线。tAydtdydtydsin)(222显然上面的微分方程不容易求解，系统分析很困难，所以常常需要引入“等效”线性系统来代替非线性系统，这种等效线性系统仅在有限的工作范围内是正确的。我们下面研究的系统就是线性系统或能等效为线性系统的非线性系统。–非线性微分方程：435、线性定常系统–如果描述一个线性系统的微分方程的系数为常数，那么称系统为线性定常系统。–如6、线性时变系统–如果描述一个线性系统的微分方程的系数为时间的函数，那么称系统为线性时变系统。–如)(22233tudtdydtyddtyd)(22233tudtdydtydtdtyd44建立合理的数学模型建立的数学模型既有准确性，又有简化性–一般应根据系统的实际结构参数及要求的计算精度，略去一些次要因素，使模型既能准确反映系统的动态本质，又能简化分析计算的工作。–除非系统含有强非线性或参数随时间变化较大，一般尽可能采用线性定常数学模型描述自动控制系统2.22.2时域模型时域模型--微分方程微分方程2.2.1.建立系统或元件微分方程的步骤确定输入输出量列写相应微分方程微分方程整理标准形式I.确定元件输入量和输出量II.根据物理或化学定律，列出元件的原始方程III.在可能条件下，对各元件的原始方程进行适当简化，略去一些次要因素或进行线性化处理IV.消去中间变量，得到描述元件输入和输出关系的微分方程V.对微分方程进行标准化处理：与输出量相关的各项置于等号左侧，而与输入量相关的置于等号右边；等号左右各项均按降幂排列；将各项系数归化为具有一定物理意义的形式图2-1建立系统或元件微分方程的步骤46例2.1机械位移系统•如图表示一个弹簧—质量—阻尼器系统。f(t)为一作用在运动部件上的外加作用力，系统产生的位移为y(t)，运动部件质量用M表示，B为阻尼器的阻尼系数，K为弹簧的弹性系数。要求写出系统在外力f(t)作用下的运动方程式。图2-2弹簧－质量－阻尼器系统①选择f(t)为系统的输入，y(t)为系统的输出。②列出原始方程式。根据牛顿第二定律，有：2221dd)()()(tyMtftftf式中f1(t)——阻尼器阻力；f2(t)——弹簧力。ttyBtfd)(d)(1在忽略弹簧质量的情况下)()(2tKytf2.2.2.微分方程47f1(t)和f2(t)为中间变量，消去中间变量，整理得)()(d)(dd)(d22tftKyttyBttyM方程两边同时除以K)(1)(d)(dd)(d22tfKtyttyKBttyKM令KBTBKMTM2则有)(1)(d)(dd)(d222tfKtyttyTttyTBM图2-2弹簧－质量－阻尼器系统例2.2RLC电路设回路电流为,由克希霍夫定律写出回路方程为：()1()()()1()()rcditLitRitutdtcutitdtc22()()()()cccrdutdutLCRCututdtdtititLRCrutcuti)()()()(,2222121tutudttduTdttudTTRCTRLTrccc则令确定元件的输入、输出Input：ur(t)Output:uc(t)–消去中间变量，得到描述网络输入输出关系的微分方程为图2-3RLC电路系统之间的微分方程式。与流入量液位高度，，，流出量为流入量为如ioiQHCHQQ该过程为水箱的截面积。建立为液位高度，其中图所示一液位流体系统例2.3HQ:Output,:Inputi设流体是不可压缩的，应满足物质守恒定律，可得：oiQQCdtdH1由流量公式得HkpgQo2为常数。对于每一种特定液体，为流体系数，为液体密度；加速度；为重力显然为节流阀前后的压力，kgp成正比；H这个压力差与液位差，其中则有，消去中间变量oQiQHkdtdHC图2-4液位流体系统50具有相同结构微分方程的系统称为相似系统例如：R-L-C电路与弹簧-质量-阻尼器系统，虽然这两个系统就系统本质而言完全不同，但其具有相同结构的微分方程。)(1)(d)(dd)(d222tfKtyttyTttyTBM)()()()(,2222121tutudttduTdttudTTRCTRLTrccc则令LRCrutcuti拉氏变换法求解步骤：1.考虑初始条件，对微分方程中的每一项分别进行拉氏变换，得到变量s的代数方程；2.求出输出量拉氏变换函数的表达式；3.对输出量拉氏变换函数求反变换，得到输出量的时域表达式，即为所求微分方程的解。2.2.3.线性定常微分方程的求解求解方法：经典法、拉氏变换法。拉氏(laplace)变换•定义：设函数f(t)当t>=0时有定义，而且积分存在，其中s是复数,则称F(s)是f(t)的象函数,即f(t)的拉氏变换。记为f(t)称为F(s)的原函数。0)()(dtetfsFst)]([)(tfLsFjjstdsesFjtfsFL)()()]([211•拉氏反变换为53•单位阶跃函数1(t)•单位阶跃函数的拉氏变换为•单位脉冲函数•单位脉冲函数的拉氏变换为0001)(1ttt10t011()0ststFsedtess1000()tttt或0()1stFstedt0t1t54•几个重要的拉氏变换f(t)F(s)f(t)F(s)δ(t)1sinwt1(t)1/scoswtt1/(s+a)21sate)(22wsw)(22wsswteatsinwteatcos22)(wasw22)(wasas)0()()(fssFtfdtd)0()0()()(222fsfsFstfdtdsfssFdttf)0()()(55•拉氏变换的基本性质(1)线性性质原函数之和的拉氏变换等于各原函数的拉氏变换之和。(2)微分性质若，则有f(0)为原函数f(t)在t=0时的初始值。)]([)]([)]()([2121tfbLtfaLtbftafL)()]([sFtfL)0()()]([fssFtfL(3)积分性质若则式中为积分当t=0时的值。)()]([sFtfL()(0)[()]FsFLftdtssdttf)((0)F56(4)终值定理即原函数的终值等于其象函数乘以s的初值。)(lim)(lim0ssFtfst(5)初值定理：(6)位移定理：a.实域中的位移定理，若原函数在时间上延迟，则其象函数应乘以b.复域中的位移定理，象函数的自变量延迟a，原函数应乘以，即)(lim)(lim0ssFtfst)()]([sFetfLsse)()]([asFtfeLatate57例2.4：用拉氏变换解微分方程vuAivuRFCHLrc11.0)0(1.0)0(1,1,11.01.0)()0()0()(])([)0()(])([)()]([2'22222ssUsUsUsUsdttudLUssUdttduLsUtuLuudtduRCdtudLCccccccccccrccc1.0)0(1.0)0('0ctcuCidtduiucurCRL12.01.011112.01.0)(11)(2.01.0)()()1()()(1.0)(1.01.0)(222222ssssssssssUsssUssUsUsssUsUssUssUsrcrcrccc原式化为：58)6866.0sin(2.0)32866.0sin(15.11)()6866.0sin(2.0]12.01.0[)23()5.0(15.0)23()5.0()5.0(1.012.01.0)32866.0sin(15.1123sin35.0223cos1]111[231)23()5.0(235.0)23()5.0(5.011115.05.05.021222225.05.05.02122222tetetutesssLsssssstetetesssLsssssssttctttt59练习–方程两边进行拉氏变换得–整理得–方程两边进行拉氏反变换得–若–则100dyTyrrtdty)()()(srsysyTsTsssTsTssrsy1111.111)()(Ttetty)(1)(rttTsTTssy11111)(TteTty1)(系统响应如图所示重点建立微分方程要掌握所涉及系统的关键公式例如：牛顿第二定律、克希霍夫定律、质量守恒定律，刚体旋转定律等建立的微分方程的标准形式特点：方法直观，但是微分方程的求解麻烦，尤其是高阶系统。)()(dd)(dd)(dd)()(dd)(dd)(dd0111101111trbtrtbtrtbtrtbtcatctatctatctammmmmmnnnnnn2.32.3复域模型复域模型––传递函数传递函数2.3.1.2.3.1.传递函数的定义与性质传递函数的定义与性质定义：线性定常系统的传递函数为零初始条件下，系统输出量的拉氏变换与系统输入量的拉氏变换之比。问题的提出传递函数不仅可以表征系统的动态特性，而且还可以用来研究系统的结构或参数变化对系统性能的影响所谓零初始条件是指1）输入量在t>0时才作用在系统上，即在时系统输入及各项导数均为零；2）输入量在加于系统之前，系统为稳态，即在时系统输出及其所有导数项为零。0t0t62•设r(t)和c(t)及其各阶导数在t=0时的值为0，即零初始条件，则对上式中各项分别求拉氏变换，可得s的代数方程为：•由定义得系统得传递函数为•设线性定常系统由下述n阶线性常微分方程描述：•式中c(t)为系统输出量，r(t)为系统输入量，ai(i=1，2，3…n)和bj(j=1,2,3….m)是与系统结构和参数有关的常系数)()(dd)(dd)(dd)()(dd)(dd)(dd0111101111trbtrtbtrtbtrtbtcatctatctatctammmmmmnnnnnn)()()()()()()()(01110111sRbssRbsRsbsRsbsCassCasCsasCsammmmnnnn)()()()(01110111sRbsbsbsbsCasasasammmmnnnn)()()()()(01110111sDsNasasasabsbsbsbsRsCsGnnnnmmmm分母中s的最高阶次n即为系统的阶次，该系统称为n阶系统。试列写网络传递函数Uc(s)/Ur(s).)()()()(22tutudttduRCdttudLCrccc)()()()(2sUsUsRCsUsULCsrccc11)()()(2RCsLCssUsUsGrc例2.5如图RLC电路，RLCi(t)ur(t)uc(t)解:零初始条件下取拉氏变换：传递函数：)()()(sUsURCsLCsrc1264性质•传递函数是复变量s的有理真分式函数，分子多项式的次数m低于或等于分母多项的次数n，所有系数均为实数；•传递函数与微分方程有相通性，可经简单置换而转换；•传递函数表征了系统本身的动态特性。（传递函数只取决于系统本身的结构参数，而与输入和初始条件等外部因素无关，可见传递函数有效地描述了系统的固有特性.）•只能描述线性定常系统与单输入单输出系统，不能表征内部所有状态的特征。•只能反映零初始条件下输入信号引起的输出，不能反映非零初始条件引起的输出。•服从不同动力学规律的系统可有同样的传递函数。•传递函数有一定的零、极点分布图与之对应，因此传递函数的零、极点分布图也表征了系统的动态性能。65传递函数的物理意义传递函数的物理意义显然，在零初始条件下，若线性定常系统的输入的拉氏变换为，则系统的输出的拉氏变换为系统的输出为由于单位脉冲输入信号的拉氏变换为所以，单位脉冲输入信号作用下系统的输出的拉氏变换为)()()(sRsGsC)}()({)}({)(11sRsGLsCLtc1)}({)(tδLsR)()(sGsC66单位脉冲输入信号下系统的输出为g(t),则可见，系统传递函数的拉氏反变换即为单位脉冲输入信号下系统的输出。因此，系统的单位脉冲输入信号下系统的输出完全描述了系统动态特性，所以也是系统的数学模型，通常称为脉冲响应函数。)}({)}({)(11sGLsCLtg67作业Page41.2-5,Duedate:29thSep.周六682.3.2.2.3.2.典型环节的传递函数典型环节的传递函数•比例环节:输出量无滞后，按比例复现输入量KsRsCsG)()()(电位器69•惯性环节该环节存在储能元件，典型惯性环节的微分方程为一阶常微分方程，其特点是当系统输入有阶跃变化时，系统输出是由零逐渐跟上，如图所示。(a)为系统的输入变化，(b)为系统的输出响应。输出按单调指数规律上升.R1C1rut1()it1TsKsRsCsGsKRsCsTsCtKrtcdttdcT)()()()()()()()()(70•积分环节输出量与输入量对时间的积分成正比•微分环节输出量与输入量的导数成正比K0R1UrUcK0UrUcR1r(t)c(t)tTssRsCsGtRsTsCtrdttdcT1)()()()()()()(TssRsCsGsTsRsCdttdrTtc)()()()()()()(积分放大器原理71例2.6：如图所示卫星姿态控制系统•对偏航角的控制其中A、B为斜对称配置的喷气发动机，推力均为F/2，成对工作。每个发动机到质心的距离为l，那么产生的力矩为T=Fl，假设卫星的转动惯量为J，角位移θ(t)为输出量，产生的力矩T为输入量，那么根据牛顿第二定律，注意到在卫星周围的环境中不存在摩擦，所以有TdtdJ22lsFsJs)()(22'21)()()(sTJslsFssG其中T’＝J/l这是由两个积分环节组成的。72•振荡环节（二阶环节）该环节存在两个储能元件，且所储两种能量可以互相转换，故动态过程表现出振荡特性22222()1()()212cnrnnUsGsUsTsTsssLRCrutcut732222222221212nnndctdctTTctrtdtdtGsTsTsss：无阻尼自然振荡频率：阻尼比n0246810121416182000.20.40.60.81StepResponseTime(sec)Amplitude1.211012121Gsss•延滞环节延滞时间（死区时间）输出量相对于输入量滞后一个恒定时间sesGtrtc)()()(75关于典型环节的几点说明关于典型环节的几点说明•一个不可分割的装置或元件可能含有若干典型环节例如：无源网络•同一元部件，若选择不同的输入量和输出量，将由不同的典型环节组成CRur（t）uc（t）结果部典型环节共同变换的全其动态性能是其中所含以及微分环节的惯性环节，时间常数为的比例环节，含有sTKRCTTsTssGT1)(,)(76有理分式形式传递函数最常用的形式是下列有理分式形式传递函数的分母多项式D(s)称为系统的特征多项式,D(s)=0称为系统的特征方程，D(s)=0的根称为系统的特征根或极点。分母多项式的阶次定义为系统的阶次。对于实际的物理系统，多项式D(s)、N(s)的所有系数为实数，且分母多项式的阶次n高于或等于分子多项式的阶次m，即n≥m。)()()(01110111sDsNasasasabsbsbsbsGnnnnmmmm2.3.3.2.3.3.传递函数的表示方式传递函数的表示方式77零极点形式将传递函数的分子、分母多项式变为首一多项式，然后在复数范围内因式分解，得n≥m（2.66）mmabk/niimiipszsksG11)()()(式中，称为系统的零点；为系统的极点；为系统的根轨迹增益。系统零点、极点的分布决定了系统的特性，因此，可以画出传递函数的零极点图，直接分析系统特性。在零极点图上，用“”表示极点位置，用“”表示零点),,2,1(mizi),,2,1(nipi78例如，传递函数的零极点图如图2.9所示。)1)(1)(3()2)(1(2685422)(232jsjssssssssssG图2.9零极点图012-1-2-3-412-1-2j79时间常数形式将传递函数的分子、分母多项式变为尾一多项式，然后在复数范围内因式分解，得000abGK/)(niivmiisTssKsG11)1()1()()(nvn212112211221)12()1()12()1()(nllllnjjvmkkkkmiisTsTsTssssKsGK式中，为传递系数，通常也为系统的放大系数；为系统的时间常数。iiT,)()(jnjimipzkK112.42.4控制系统结构图控制系统结构图2.4.1结构图的基本组成微分方程、传递函数等数学模型，都是用纯数学表达式来描述系统特性，不能反映系统中各元部件对整个系统性能的影响。定义:由具有一定函数关系的环节组成的，并标明信号流向的系统的方框图，称为系统的结构图。结构图又称为方框图、方块图等，既能描述系统中各变量间的定量关系，又能明显地表示系统各部件对系统性能的影响。•方框（环节）–方框表示对信号进行数学变换。方框中写入元部件或系统的传递函数。系统输出的象函数等于输入的象函数乘以方框中的传递函数或者频率特性•信号线–信号线是带有箭头的直线，箭头表示信号的流向，在直线旁边标记信号的时间函数或象函数。这里的信号引出与测量信号一样，不影响原信号，所以也称为测量点.•综合点（比较点）–比较点表示对两个以上的信号进行加减运算，“＋”表示相加，“－”表示相减。进行相加或相减的量应具有相同的量纲单位•分支点（引出点）–引出点表示信号引出或测量的位置。从同一位置引出的信号在数值和性质方面完全相同。(),()utUs(),()utUs(),()utUs(),()utUs(),()rtRs()()()()utrtUsRsG(s)(),()utUs(),()ctCs82结构图特点•结构图是方块图与微分方程（传函）的结合。一方面它直观反映了整个系统的原理结构（方块图优点），另一方面对系统进行了精确的定量描述（每个信号线上的信号函数均可确定地计算出来）•能描述整个系统各元部件之间的内在联系和零初始条件下的动态性能，但不能反映非零条件下的动态性能•结构图最重要的作用：计算整个系统的传函•对同一系统，其结构图具有非唯一性；简化也具有非唯一性。但得到的系统传函是确定唯一的.•结构图中方块≠实际元部件，因为方框可代表多个元件的组合，甚至整个系统83结构图的绘制结构图的绘制•建立控制系统各元部件的微分方程•对各元件的微分方程进行拉氏变换，并作出各元件的方框图和比较点。•置系统输入量于左端，输出量于右端，便得到系统结构图。•从与系统输入量有关的比较点开始，依据信号流向，把各元部件的结构图连接起来。例2.8绘制如图所示RC网络的结构图。中间变量：i,i1,i2;信号量：ur,uc根据电路定律，得到以下方程图2.13RC网络C1R2Rrucui1i2i)()(2sIRsUc)()(1112sIRsICs)()()(21sIsIsI)()()(11sUsIRsUcr84按照上述方程，可以分别绘制相应元件的结构图，如图(a)～(d)所示。然后，根据相互关系将这些结构图在相同信号处连接起来，就得到整个系统的结构图。)()(2sIRsUc)()(1112sIRsICs)()()(21sIsIsI)()()(11sUsIRsUcr11R)(sUr)(1sI)(sUc2R)(sI)(sUc1R)(1sICs)(2sI)(1sI)(2sI)(sI11R)(sUr)(1sI)(sUc2R)(sUc1RCs)(2sI)(1sI)(sI(a)(b)(c)(d)(e)练习绘出RC电路的结构图。)s(IR)s(U)s(U11crsC)s(I)s(U11cUr(s)Uc(s)I1(s)1/R11/sC1(-)R1C1i1(t)ur(t)uc(t)为了便于系统分析和设计，常常需要对系统的复杂的结构图作等价变换，或者通过变换使系统结构图简化，求取系统的总传递函数。因此，结构图变换是控制理论的基本内容。2.4.2结构图的化简等效变换的原则结构图的变换应按等效原则进行。所谓等效，即对结构图的任一部分进行变换时，变换前后输入输出的数学关系保持不变结构图的基本组成形式串联连接并联连接反馈连接87等效变换的法则–串联连接的等效变换传递函数的串联连接，其等效传递函数为这些传递函数的积。–上述结论可以推广到多个传递函数的串联，即n个传递函数依次串联的等效传递函数，等于n个传递函数的乘积。1Gs2GsRsUsCs12GsGsRsCs121212,()UsGsRsCsGsUsCsGsGsRsGsRsGsGsGs1Gs2GsRs12......nGsGsGsRsCs……nGsCs88–并联连接的等效变换传递函数的并联连接，其等效传递函数为这些传递函数的和。–上述结论可以推广到多个传递函数的并联，即n个传递函数并联的等效传递函数，等于n个传递函数的和。12GsGsRsCs1Gs2GsRs1Cs2CsCs1122121212,CsGsRsCsGsRsGsCsCsGsGsRsGsGsGs12...nGsGsGsRsCs1Gs2GsRs1Cs…2CsCsnGs3Cs89–反馈连接的等效变换GsHsRsCsEsBs,,11BCsGsEsBsHsCsEsRsBsCsGsRsHsCsGsHsCsGsRsCsGsGsRsGsHs1GsGsHsRsCs90–比较点（综合点）和引出点的移动在系统结构图简化的过程中，有时为了便于进行方框的串联、并联或者反馈连接的计算，需要移动比较点或引出点的位置。•比较点前后移动QGsCsRs1CGsRQCGsRGsQGsRQQGsCs1Gs91–引出点前后移动GsCsRsCsGsCsRsGsCsCsRsGs92注意•对综合点和分支点进行移动位置，消除交叉回路。但在移动中一定要注意以下几点：–①必须保持移动前后信号的等效性；–②相邻综合点可以互相换位和合并；–③相邻分支点可以互相换位；–④综合点和分支点之间一般不宜交换位置。93序号原结构图等效原结构图等效法则1串联等效2并联等效3反馈等效)(1sG)(2sGRC)(1sG)(2sGRC)()()()(21sRsGsGsC)(1sGRC)(2sG)(1sG)(2sGRC)()]()([)(21sRsGsGsC)(1sG)(2sGRC)()(1)(211sGsGsGRC)()(1)()()(211sGsGsRsGsC944等效单位反馈5比较点前移6比较点后移7引出点前移)(1sG)(2sGRC)(1sG)(2sGRC)(12sG)()(1)()()(1)()(21212sGsGsGsGsGsRsC)(sGRCY)(sG)(1sGRCY)(])()()([)()()()(sGsGsYsRsYsGsRsC)(sGRCY)(sGRCY)(sG)()()()()()]()([)(sGsYsGsRsGsYsRsCRCC)(sG)(sGRC)(sGC)()()(sGsRsC95•8引出点后移9交换和合并比较点10交换比较点和引出点（一般不采用)11负号在支路上移动RCR)(sG)(sGRR)(1sG)(1)()()(sGsGsRsR)()()(sGsRsCC1R2R3R1EC1R2R3R1EC1R2R3R)()()()(321sRsRsRsCCC1R2RC1R2RC2R)()()(21sRsRsCRC)(sG)(sHE(S)RC)(sG)(sHE(S)-1+)()1()()()()()()(sCsHsRsCsHsRsE632236G)GG(G4554GGG154236236GGG1GG例2.9G4(s)(-)G2(s)G6(s)(-)C(s)R(s)G3(s)G5(s)G1(s)97例2.10：试化简下述系统结构图，并求传递函数C(s)/R(s)•显然若不移动比较点或引出点的位置就无法化简。3Gs3HsRs4GsCs2Gs1Gs3Hs1HsH2(s)98–首先将间的引出点后移到方框的输出端–接着将组成的内反馈网络简化，其等效传递函数为34,GsGs343,,GsGsHs34343431GsGsGsGsGsHs3Gs3HsRs4GsCs2Gs1Gs3Hs1HsH2(s)3Gs3HsRs4GsCs2Gs1Gs3Hs1Hs41GsH2(s)99–得到图为–然后将组成的内反馈网络简化，其等效传递函数为：23424,,GsGsHsGs234233432321GsGsGsGsGsGsHsGsGsHs＋34GsRsCs2Gs1Gs1Hs34HsGsH2(s)/G4(s)3Gs3HsRs4GsCs2Gs1Gs3Hs1Hs41GsH2(s)100–得到图为–最后将求得其传递函数为：RsCs23Gs1Gs1Hs1234232343123411AGsGsGsGsGsGsGsHsGsGsHsGsGsGsGsHs＋34GsRsCs2Gs1Gs1Hs34HsGsH2(s)/G4(s)101作业Page42.2-6(绘制(a).(b).的方框图）,2-12Duedate:11thOct.周四102练习：试化简下述系统结构图，并求传递函数C(s)/R(s)•显然化简该结构图也需要移动比较点和引出点，需要注意得是，引出点和比较点之间是不宜随便移动的。因此我们将比较点前移，将引出点后移。–得到图为2GsRsCs1Gs1Hs2GsCs1Gs1Hs11Gs21GsRs103–将两个比较点合并，并将求出的等效传递函数：–得到图为–得到系统等效传递函数：2GsCs1Gs11211HsGsGs11211HsGsGs12121211ACsGsGsGsRsGsGsGsGsHs2GsCs1Gs1Hs11Gs21GsRs)(),(/),(/sHsGsG121112.4.3闭环系统的结构图和传递函数•控制系统常采用反馈结构，又称闭环控制系统。通常，控制系统会受到两类外作用信号的影响。一类是有用信号，或称为输入信号、给定值、参考输入等，常用r(t)表示；另一类则是扰动，或称为干扰、噪声等，常用n(t)表示。•通过对反馈控制系统建立微分方程模型，直接在零初始条件下进行拉氏变换，可求取反馈控制系统的传函。•通过对反馈控制系统结构图简化也能求传函。图2.18反馈控制系统)(sE)(1sG)(sR)(sN)(sC)(2sG)(sH)(sB)()()()()()()()()(sGsNsCsPsGsGsRsCsPnr221对扰动而言：对输入而言：)()()()(sHsCsBsr对输入而言：反馈通道传递函数从输出端反送到参考输入端的信号通道，称为反馈通道图2.18反馈控制系统)(sE)(1sG)(sR)(sN)(sC)(2sG)(sH前向通道传递函数前向通道是指从输入端到输出端的通道)(sB系统的开环传递函数上图中将反馈的输出通路断开，反馈信号对于参考输入信号的传递函数称为开环传递函数。这时前向通路传递函数与反馈通路传递函数的乘积为该系统的开环传递函数。)()()()()()(sHsGsGsEsBsG21图2.18反馈控制系统)(sE)(1sG)(sR)(sN)(sC)(2sG)(sH)(sB作用下系统的闭环传递函数•令，这时系统结构图如上图，系统传递函数为：•系统输出为：作用下系统的闭环传递函数•令，这时系统结构图如上图，系统传递函数为：•系统输出为：()rt2GsBsCs1GsHsRs0nt12121GsGsCsRsGsGsHs()nt0rt2121GsCsNsGsGsHs2GsCs1GsHsNs)()()()()()()()(sHsGsGsGsGsRsCsr21211)()()()()()()(sHsGsGsGsNsCsn2121108系统总输出根据线性系统的叠加原理，系统的总输出应为各外作用引起输出的综合因而得到系统总输出为：)]()()()()([)()()()()()()()()()()()()()()()()()()(sNsGsRsGsGsHsGsGsNsHsGsGsGsRsHsGsGsGsGsNssRssCn2212121221211111109闭环系统的误差传递函数误差定义为被控量的测量输出和给定输入之差或•作用下的误差，输入结构图–误差传递函数•n(t)作用下系统的误差传递函数，输入结构图–误差传递函数–总误差()()()etrtbt()bt()rtEsRsBs()rtEs2GsRs1GsHs1Gs2GsHsNsEs)()()(11)()()(21sHsGsGsRsEse)()()(1)()()()()(212sHsGsGsHsGsNsEsen)()()()()(sNssRssEene110闭环系统的特征方程•上面导出闭环传递函数及误差传递函数虽然各不相同，但是他们的分母却是一样的。均为：令并称其为闭环特征方程。将其改写为如下形式：•对给定的系统而言，特征多项式是唯一的，即闭环极点的分布是唯一的。•闭环系统的极点与控制系统的瞬态响应和系统的稳定性密切相关•特征多项式与开环传函相关，因此其动态特性可用开环传函分析121GsGsHs1210DsGsGsHs这是闭环控制系统各种传递函数都具有的的规律性，称其为特征多项式00111asasasnnn0)())((21npspsps可以是实数或共轭复数，称为特征方程的根，或称为闭环系统的极点nppp、、21111例2.11如图所示位置随动系统的方块图，求系统在给定值θr(t)作用下的闭环传递函数及在负载力矩ML作用下的闭环传递函数，并求两信号同时作用下，系统总输出c(t)的拉氏变换式。解（1）求作用下系统的闭环传递函数)()(ssrc令ML=0，运用串联及反馈法则，可求得：amsaaemamsarciRKKKsRKKBJsiRKKKsss/)/(/)()()(2θr(t)112（2）求ML作用下系统的闭环传递函数)()(sMsLc令θr(t)=0，系统以ML为输入的方块图如图(a)所示。经方块图变换后如图(b)所示可求得：(a)(b)113amsaaemLcniRKKKsRKKBsJisMss/)/(/1)(2)()(（3）系统在给定值θr(t)作用及在负载力矩ML作用下的总输出为两部分迭加，即)()()()()(sMssssCLnr1142.52.5状态空间模型（现代控制理论）状态空间模型（现代控制理论）定义在状态空间中以状态向量或状态变量描述系统的方法称为系统的状态空间模型（内部表达）。优点–能完全表达出系统的全部状态和性能（内部和外部）–能了解系统内部状态的变化特性–容易考虑初始条件–适用范围广:时变系统，非线性系统，多输入多输出–便于设计115预备知识——有关矩阵的微分1、向量函数对数量函数的导数2、矩阵函数对数量函数的导数3、数量函数对向量的导数4、向量函数对向量的导数5、矩阵函数对向量的导数1161、向量函数对数量函数的导数2、矩阵函数对数量函数的导数nnxxxdtXdxxxX2121定义：)()()()()()()()()()()()()()()()()()(212222111211212222111211tatatatatatatatatadtdAtatatatatatatatataAnnnnnnnnnnnn定义：1173、数量函数对向量的导数4、向量函数对向量的导数TnTnnxfxfxfdxdfxxxXxxxf212121),,,,(定义：nnnnnnnnxaxaxaxaxaxaxaxaxadxdAxxxXxaxaxaxA212222111211TT21T21)()()()(定义：1185、矩阵函数对向量的导数lmnnTnnlmmlmmllxAxAxAdxdAxxxxxaxaxaxaxaxaxaxaxaxA21121212222111211定义：)()()()()()()()()()(1192.5.1.状态变量表达式相关概念如图所示的RLC电路，其输入电压为ur(t)，该电路中的四个物理量i(t)、uR(t)、uL(t)、uC(t)反映着系统各方面的特征，根据线性电路知识，这个电路有两个储能元件，即电感L和电容C，因此只能有两个物理量是独立的，而其余的物理量必能用这两个独立的物理量来表示。当选i(t)、Uc(t)为独立变量时，则其它变量可表示为：)()(tRituR)()()()(tRitututuCrL)()()()()()(tRitutudttdiLtidttduCCrC由解微分方程可知，如果已知初始条件i(0)、uc(0)以及t>0的ur(t),那么在t>0后的任一时刻的解就完全被确定120如方程组采用状态向量表示时,令为系统输入，)(),()(),(21tututxtixrC122111)(1)(1)()(xCxtuLtxLtxLRtxr)()()()()()(tRitutudttdiLtidttduCCrC(状态方程)如果以uC(t)为系统输出，用y表示，则有)(2txy(输出方程)系统输出也可能并不一定是状态变量，但前面提到，其它的量如uR(t)或uL(t)等一定能用状态变量来表示。即输出可以写成状态变量的线性组合,因此输出方程一定是代数方程121写为矩阵形式如21212110)(01011xxytuLxxCLLRxxr状态空间模型21xxx011CLLRA01LB10CCxyBuAxxr122基本概念–状态：系统过去、现在和将来的状况。–状态变量：状态变量指能确定系统运动状态的最少数目的一组变量。–状态向量：若以n个状态变量做为向量的分量，则称为状态向量。–状态空间：以状态变量为基构成的n维空间。–状态方程：描述系统状态变量与输入变量之间关系的一阶微分方程组称为状态方程。()Xt12,,......,nxtxtxt()Xt12,,......,nxtxtxt123状态方程的一般形式–单输入线性定常连续系统式中常系数与系统特性有关。上式可以写成向量矩阵形式：其中1111122112211222221122nnnnnnnnnnnxtaxtaxtxtbutxtaxtaxtxtbutxtaxtaxtxtbutaaa111,,;,,;nnnabba111112112221222212(),,,nnnnnnnnnxxaaabxxaaabxtxtAbxxaaabxtAxtbut124–多输入线性定常连续系统向量矩阵形式为：其中BuAxx11111221111122122112222211222211221122nnppnnppnnnnnnnnnppxaxaxxbububuxaxaxxbububuxaxaxxbububuaaapnpnnppnnnnnnnuuuubbbbbbbbbBaaaaaaaaaAtxtxtxtx2121222211121121222211121121,,,)()()()(125输出方程：系统输出量与状态变量、输入量的关系称为输出方程。输出量由系统任务确定或给定–单输出线性定常连续系统输出方程的一般形式为式中常系数与系统特性有关。其向量矩阵形式为：–多输入－多输出系统的输出方程的一般形式为•其向量矩阵形式为：12,,ncccd；1112nnytcxtcxtcxtdutytcxtdutyCxDupqpqqnqnqqqppnnppnnudududxcxcxcyudududxcxcxcyudududxcxcxcy22112211222212122221212121211112121111126状态空间表达式：状态方程与输出方程的组合称为状态空间表达式，又称动态方程。–A(t):系统矩阵（状态矩阵）–B(t):控制矩阵（输入矩阵）–C(t):观测矩阵（输出矩阵）–D(t):直接传递矩阵xAxByCxDuuxAxbuycxdu―多输入－多输出系统状态空间表达式的一般形式为–单输入－单输出系统状态空间表达式的一般形式为127对于一般的非线性系统，其状态方程和输出方程可能还是状态和输入的非线性函数),,,,(),,,,,(111111tuuxxfxtuuxxfxpnnnpn因此状态方程和输出方程可用如下向量方程表示),,(),,(tuxgytuxfx128对于本节主要讨论的线性定常系统来说，状态空间模型的标准形式是DuCxyBuAxx线性系统的状态空间表达式动态结构图129对于本节主要讨论的线性定常系统来说，状态空间模型的标准形式是DuCxyBuAxx系统A输入u输出y状态Xa)结构关系图DBC1302.5.22.5.2由微分方程建立状态变量表达式由微分方程建立状态变量表达式步骤：–直接根据系统的物理机理建立相应的微分(连续系统）或差分（离散系统）方程组。–针对微分方程，定义一组状态变量，建立状态方程，并根据系统输出和状态之间的关系，建立系统的输出方程。状态变量的选取1.状态变量的选取是非唯一的。2.选取方法（1）可选取初始条件对应的变量或与其相关的变量作为系统的状态变量。（2）可选取独立储能（或储信息）元件的特征变量或与其相关的变量作为控制系统的状态变量。（如电感电流i、电容电压uc、质量m和速度v等。131例2.14：试确定下图中两个电网络的独立状态变量。图中分别为输入电压、电流，为输出电压，为电容端或电感电流。–图(a)由于因此三个变量中只有两个是独立的，系统的状态变量可以是三者中的任意两个。ixui、yu1x2xy3x(a)1230xxx132–图(b)由于(b)中有，因此，它只有一个独立的状态变量，任意取中的一个即可。1xy2xu(b)12xx12,xx133例2.15：由质量块、弹簧、阻尼器组成的机械位移系统如图示•有力F及阻尼器汽缸速度V两种外作用，另输出量为：质量块位移、速度和加速度。试写出该双输入－三输出机械位移系统的状态空间表达式。图中m、k、f分别为质量、弹簧的弹性模量、阻尼系数，x为位移。解：根据牛顿力学得到该系统的微分方程为：它是二阶系统，选择质量块的位移和速度为状态变量。令系统的三个输出量为，FVxxxkfmmxfxVkxF12,xxxx11223yxxyxxyx134由系统的微分方程可导出下列状态方程：其向量－矩阵形式为122211211xxxxfxVkxFmkffxxFVmmmm112201001xxFkffxxVmmmm11223100001001yxFyxVykffmmmm状态变量一般选可反映储能元件能量变化的量（eg：电感电流、电容电压、位置、速度）135线性微分方程中不含有输入函数导数项的系统的状态空间表达式–选取状态变量：–则有：1123,,,,nnxyxyxyxy12231111nnnnnnnxyxxyxxyxxyayaybu)()()()()(001)1(1)(tubtyatyatyatynnn136–系统状态空间表达式为：cxybuAxx)()()()(21txtxtxtxn1210100001000010naaaaA000bb001c137–根据上式绘制的状态变量之间关系的方块图如图所示，每个积分器的输出都是对应的一个状态变量，状态方程由积分器的输入输出关系确定，输出方程在输出端给出：)()()()()(001)1(1)(012110tubtyatyatyatyubxaxaxaxnnnnnn138例2.16：设一控制系统的动态过程用微分方程表示为式中u,y分别为系统的输入和输出信号，试求系统的状态空间描述。–解：选取状态变量为–则有：uyyyy66116yxyxyx321,,uxxxxxxxx6611632133221139–将上式写成矩阵微分方程形式uxxxxxx6006116100010323211321001xxxy140系统输入量中含有导数项–其一般形式为：–若选取状态变量–则得到1123,,,,nnxyxyxyxy122311111011nnnnnnnnnnnxyxxyxxyxxyaxaxbubububu)(')()()()(01)1(1)(01)1(1)(tububububtyatyatyatynnnnnnn在状态方程中将会出现输入导数项141–应选择以下n个变量作为一组状态变量–则状态变量如下niuhxxuhyxiii,,3,21101uhuhuhyuhxxuhuhuhyuhxxuhuhuhyuhxxuhuhyuhxxuhyxnnnnnnnnnnnnnn1)2(1)1(0)1(112)3(1)2(0)2(2212102231011201式中是n个待定常数.110,nhhh142输出方程uhxy01状态方程uhxxuhxxuhxxuhxxnnnnnn11212232121对最后一个方程处理，uhuhuhyuhxxnnnnnnn1)1(1)(0)(11143uhuhuhububububyayayayauhuhuhyxnnnnnnnnnnnnnnnn1)1(1)(001)1(1)(01)2(2)1(11)1(1)(0)()(并将y(n）用下式代入)(')()()()(01)1(1)(01)1(1)(tububububtyatyatyatynnnnnnn得到：144将上式中所有的输出项以及输出的导数项都用状态和输入的各阶导数项表示有uhahahahabuhahahbuhahbuhbxaxaxaxaxnnnnnnnnnnnnnnnnnn)()()()(001122110)2(021122)1(0111)(01122110uhuhuhububububyayayayauhuhuhyxnnnnnnnnnnnnnnnn1)1(1)(001)1(1)(01)2(2)1(11)1(1)(0)()(145令上式中u的各阶导数项的系数为零，则有0132211102112201110hahahabhhahabhhabhbhnnnnnnnnnnn令则有001122110hahahahabhnnnnnuhxaxaxaxaxnnnnnn1122110146–将上式改为矩阵向量形式为：–其中ducxybuAxx1210100001000010naaaaAnhhhb21001cd=h0＝bn147绘制出状态变量之间关系的方块图如图所示148例2.17：•设一控制系统的动态过程用微分方程表示为式中u,y分别为系统的输入和输出信号，试求系统的状态空间表达式。–解：选择状态变量为uuyyyy64016064019218uhxxxxuhxxuhxxuhxy332132321210118192640uhxxuhxxuhyx2231120114900160640181926403210210bbbbaaa由题知：16000011212022130hahabhhabhbh22401601864000112203hahahabh150根据上式写出控制系统空间表达式为18192640100010A22401600bd=03213213210012240160018192640100010xxxyuxxxxxx001c151例2.18：设一控制系统的动态过程用微分方程表示为式中u,y分别为系统的输入和输出信号，试求系统的状态空间表达式。画出系统的结构图解：由题得3423yyyyuuu01134213210210bbbbaaa310011212022130hahabhhabhbh131234300112203hahahabh152–写出状态空间表达式为–系统结构图如下0101001312413100xxuyx1s1s4u3x2x1xy131s-32153一般形式：当式中bn=0时，还可以按如下规则选择另一组状态变量。设)(')()()()(01)1(1)(01)1(1)(tububububtyatyatyatynnnnnnn1,,3,2,1,1niubyaxxyxiiiin154则得到ubyaubyaubyayubyaxxubyaubyaubyayubyaxxubyaubyayubyaxxubyayubyaxxnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn11)3(2)3(2)2(1)2(1)1(112122)4(2)4(2)3(1)3(1)2(223222112212111111,,3,2,1,1niubyaxxyxiiiin155因此可以得到（n-1）个状态方程ubxaxxubxaxxubxaxxnnnnnnnnnnn11122221111输出方程为nxy156ubyaubyaubyayubyaxxnnnnnnnnn11)3(2)3(2)2(1)2(1)1(1121对下式求导用代入后)(')()()()(01)1(1)(01)1(1)(tububububtyatyatyatynnnnnnnubxaxn001状态方程为ducxybuAxx157ducxybuAxx12101000010001000naaaaA110nbbbb100cd=0158状态变量之间关系的方块图159例2.19试求的状态空间表达式。00160640181926403210210bbbbaaauuyyyy64016064019218因为此系统为三阶系统，而b3=0，所以可以选择状态变量322322331131123030118160192640640xxubxaxxuxxubxaxxuxubxax3xyuyxubyaxxyxubyaxxyx1601921821121322323160321321321100016064018101920164000xxxyuxxxxxx所以状态空间表达式为对于一个给定的系统而言，状态变量的选取并不是唯一的。1612.5.32.5.3由传递函数建立状态变量表达式由传递函数建立状态变量表达式1、设线性定常系统的传递函数为有理真分式(bn为零)0)1(1)(01101)1(1011101101111)()()()()()()()()()()(axaxuasassUsXbxbxbybsbsbsXsYasasbsbsbsUsXsXsYsUsYsGnnnnnnnnnnnnnnn＝令0110111)()()(asasbsbsbsUsYsGnnnnn162nnnnnnnnnnnnxxxbbbyuxxxaaaxxxuxaxaxaxxxxxxxxx21110211102112110)()1(1211001000010令163•为非有理真分式时：（bn不为零）01110111)()()(asasasabsbsbsbsUsYsGnnnnnnnn)('''')(01110111sGbasasasbsbsbbsGnnnnnnnducxybuAxx由可知：bn就等于状态方程中的直接矩阵d)('sG而为有理真分式因此我们只要能由一个有理真分式的传递函数求相应的状态空间表达式的话，那么对非有理真分式求状态空间表达式，只需增加一个直接矩阵d即可164uxy012211''''bsbsbsbnnnn01111asasasnnnbn165这种形式的状态空间表达式被称为可控标准型。buAxxcxy1210100001000010naaaaA100b110'''nbbbc166•由于为有理真分式，即对应的微分方程中输入导数项的最高阶等于零)('sGnb'因此也可以采用式的方式选择状态变量，那么状态空间表达式为1,,3,2,1,1niubyaxxyxiiiinbuAxxcxy12101000010001000naaaaA110'''nbbbb100c167这种形式的状态空间表达式被称为可观测标准型buAxx12101000010001000naaaaA110'''nbbbb100ccxy1682、传递函数以极点形式给出•系统传递函数只有单实极点（没有重极点）)()()(01110111sDsNasasasbsbsbsGnnnnn系统特征方程可表示为)())(()(21nssssD通过部分分式展开成下列形式niiiscsUsYsG1)()()(169niiiscsUsYsG1)()()(isiissGc)])(([为G(s)在极点λi处的留数因此有)()(1sUscsYniii选择状态变量为)(1)(sUssXiini,,2,1输出为niiisXcsY1)()(以上两式整理后，取反拉氏变换得：)()()(tutxtxiiini,,2,1)()(1txctyniii170写成矩阵形式有对角阵标准型nnnnnxxxcccyuxxxxxx212121212111100171如果状态变量选择为)()(sUscsXiii那么系统输出则为niisXsY1)()(同样，经过反拉氏变换并展成矩阵形式有对角阵标准型nnnnnxxxyucccxxxxxx212121212111100172•系统传递函数含有重实极点情况假设极点λ1为三重极点，其它均为单实极点，即λ4、λ5、…λn，那么系统特征方程可表示为)()()()(431nssssD传递函数可以通过部分分式展开成下列形式niiiscscscscsUsYsG411321123111)()()()()()(那么系统输出为)()()()()()()()(411321123111sUscsUscsUscsUscsYniii173如果选择状态变量为)(1)(13sUssX)(1)(312sXssX)(1)(211sXssX)(1)(sUssXiini,,5,4输出为niiisXcsXcsXcsXcsY4313212111)()()()()(174整理得)()()(sUsXssXiiini,,4,3)()()(3212sXsXssX)()()(2111sXsXssX175对上式反拉氏变换并整理得约当标准型nnnnnxxxxxcccccyuxxxxxxxxxx432141312114321411143211110000101称重极点对应的111001001为约当块1762.5.4、由状态空间表达式求传递函数阵DuCxyBuAxx若对上式求拉氏变换，并令初始条件为零，则有)()()(sBUsAXssX)()()(sDUsCXsY整理式得)()()(sBUsXAsI)()()(1sBUAsIsX根据传递函数阵的定义有DBAsICsUsYsG1)()()()(第三章线性系统的时域分析第三章线性系统的时域分析分析和设计控制系统的首要任务是建立系统的数学模型。一旦获得合理的数学模型，就可以采用不同的分析方法来分析系统的性能。经典控制理论中常用的工程方法有经典控制理论中常用的工程方法有时域分析法时域分析法频率特性法频率特性法根轨迹法根轨迹法分析内容分析内容瞬态响应瞬态响应稳定性稳定性稳态性能稳态性能时域分析法在时间域内研究系统在典型输入信号典型输入信号的作用下，其输出响应输出响应随时间变化规律的方法。对于任何一个稳定的控制系统，输出响应含有瞬态分量和稳态分量。1783.1时间响应性能指标3.2一阶系统的时域响应3.3二阶系统的时域响应3.4系统的稳定性分析3.5系统稳态性能分析1793.13.1时间响应性能指时间响应性能指标标工程实际中，有些系统的输入信号是已知的（如恒值系统），但对有些控制系统来说，常常不能准确地知道其输入量是如何变化的（如随动系统）。因此，为了方便系统的分析和设计，使各种控制系统有一个进行比较的统一的基础，需要选择一些典型试验信号作为系统的输入，然后比较各种系统对这些输入信号的响应。常用的试验信号有阶跃信号、斜坡信号、抛物线信号、脉冲信号及正弦信号。这些信号都是简单的时间函数，并且易于通过实验产生，便于数学分析和试验研究。3.1.13.1.1典型输入信号典型输入信号㈠阶跃函数阶跃函数的定义是000)(ttAtr对系统输入阶跃函数就是在t=0时，给系统加上一个恒值输入量，如图所示。若A=1，称为单位阶跃函数，记作1(t)0001)(1ttt阶跃函数的拉氏变换为sAesAdteAtrLsRstst00)]([)(单位阶跃函数的拉氏变换为R(s)=1/s。A0t㈡斜坡函数斜坡函数也称等速度函数。其定义为输入斜坡函数相当于对系统输入一个随时间作等速变化的信号，其图形如图所示。若A=1,则称之为单位斜坡函数。斜坡函数等于阶跃函数对时间的积分。斜坡函数的拉氏变换为单位斜坡函数的拉氏变换为R(s)=1/s2000)(ttAttr0200)]([)(sAdtesAesAtdtAtetrLsRstststA10t㈢抛物线函数抛物线函数也称加速度函数，其定义为输入抛物线函数相当于对于系统输入一个随时间做等加速变化的信号，其图形如图所示。若A=1,称之为单位抛物线函数。抛物线函数等于斜坡函数对时间的积分。抛物线函数的拉氏变换为单位抛物线函数的拉氏变换为R(s)=1/s3000221tAtttr)(3st00st20st221sAdtesAtets2AdteAttrLsR)]([)(t10A21㈣脉冲函数脉冲函数的定义为脉冲函数在理论上（数学上的假设）是一个脉宽无穷小，幅值无穷大的脉冲。在实际中，只要脉冲宽度极短即可近似认为是脉冲函数。如图所示。脉冲函数的积分，即脉冲的面积为t0t0t0Atr和)(AtAdtAdttr0000limlim)(0tA–理想的单位脉冲信号实际上是不存在的，只具有数学意义。任意形式的外作用可以看作是在不同时刻存在的，强度不同的无限多个脉冲函数的叠加。184（t）函数的图形如右图所示。脉冲函数的积分就是阶跃函数。脉冲函数的拉氏变换为单位脉冲函数的拉氏变换为R(s)=1。0st00st0stAdtetAdtetAdtetAtrLsR)()()()]([)(t0(t)1当A=1时，即面积为1的脉冲函数称为单位脉冲函数，记为(t)t0t0t01t,/)(㈤正弦函数正弦函数也称谐波函数，表达式为用正弦函数作输入信号，可求得系统对不同频率的正弦输入的稳态响应。正弦输入的拉氏变换为0t00ttASintr)(220tjs0tjs0sttjtj0stsAjs1js1j2Ajsejsej2Adteeej2AdtteASintrLsR][][)()]([)()()(186如果控制系统的实际输入大部分是随时间逐渐增加的信号，则选用斜坡函数较合适；如果作用到系统的输入信号大多具有突变性质时，则选用阶跃函数较合适。需要注意的是，不管采用何种典型输入型号，对同一系统来说，其过渡过程所反应出的系统特性应是统一的。这样，便有可能在同一基础上去比较各种控制系统的性能。此外，在选取试验信号时，除应尽可能简单，以便于分析处理外，还应选择那些能使系统工作在最不利的情况下的输入信号作为典型实验信号。本章主要讨论控制系统在阶跃函数、斜坡函数、脉冲函数等输入信号作用下的输出响应。1873.1.23.1.2动态性能指标动态性能指标动态性能动态性能延迟时间td：响应曲线第一次达到其稳态值一半所需时间。上升时间tr：响应从稳态值的10%上升到稳态值90%所需时间；对有振荡系统亦可定义为响应从零第一次上升到稳态值所需时间。上升时间是响应速度的度量。ptr0.5y(t)tdtp01tst稳态误差188峰值时间tp：响应超过其稳态值到达第一个峰值所需时间。调节时间ts：响应到达并保持在稳态值内所需时间。超调量%：响应的最大偏离量h(tp)与稳态值h(∞)之差的百分比，即%100)()()(%hhthpptr0.5y(t)tdtp01tst稳态误差稳态性能：由稳态误差ess描述。1893.23.2一阶系统的时域响应一阶系统的时域响应由一阶微分方程描述的系统称为一阶系统.典型闭环控制一阶系统如图所示.其中是积分环节，T为它的时间常数。Ts1一阶系统的结构图C(s)-R(s)Ts11Ts1Ts11Ts1sRsCs)/()/()()()(典型的一阶系统是一个惯性环节,输出为)()().()(sR1Ts1sRssC一般地，将微分方程为传递函数为的系统叫做一阶系统。)()()(trtcdttdcT11)()(TssRsC190)()()(tutudttduCRrccTssCRsUsUrc1111)()(R(s)C(s)E(s)(-)1/Ts传递函数:结构图：微分方程:Ri(t)C)(tur)(tuc如RC电路:在零初始条件下，利用拉氏反变换或直接求解微分方程，可以求得一阶系统在典型输入信号作用下的输出响应。191s1sR)(T1s1s1s11Ts1sC.)(Tte1tC)()(0t实际中，常以输出量达到稳态值的95%或98%的时间作为系统的响应时间（即调节时间）,这时输出量与稳态值之间的偏差为5%或2%。在整个工作时间内，系统响应都不会超过稳态值。由于该响应曲线具有非振荡特征，故也称为非周期响应，如下图所示。3.2.13.2.1单位阶跃响应单位阶跃响应设系统的输入为单位阶跃函数r(t)=1(t),其拉氏变换为,则输出的拉氏变换为当初始条件为零时，一阶系统单位阶跃响应的变化曲线是一条单调上升的指数曲线。192图中指数响应曲线的初始（t=0时）斜率为.实际上，响应曲线的斜率是不断下降的，经过T时间后，输出量C（T）从零上升到稳态值的63.2%。经过3T～4T时，C（t）将分别达到稳态值的95%～98%。可见，时间常数T反应了系统的响应速度，T越小，输出响应上升越快，响应过程的快速性也越好。斜率T11C(t)0.95T3T0.632一阶系统的单位阶跃响应T1系统单位阶跃响应曲线可用实验的方法确定，将测得的曲线与上图作比较，就可以确定该系统是否为一阶系统或等效为一阶系统。193)()(0te1tctT1j0p=-1/TS平面(a)零极点分布c(t)0.6320.8650.950.982初始斜率为1/Tc(t)=1-e-t/T0tT2T3T4T1(b)单位阶跃响应曲线特点：1）可以用时间常数去度量系统的输出量的数值；2）初始斜率为1/T；3）无峰值时间，无超调；稳态误差ess=0。性能指标：延迟时间：td=0.69T上升时间：tr=2.20T调节时间：ts=3T(△=0.05)或ts=4T(△=0.02)输入r(t)=1(t)，输出194式中，t-T为稳态分量，为瞬态分量，当t→∞时，瞬态分量指数衰减到零。一阶系统的单位斜坡响应曲线如图所示。T1sTsTs1s11Ts1sC22)(TtTtTtTeTte1TtTeTttC)()(（（t≥t≥00））TTttTTC(t)C(t)r(t)=tr(t)=too一阶系统的单位斜坡一阶系统的单位斜坡响应响应TtTe3.2.23.2.2单位斜坡响应单位斜坡响应设系统的输入为单位斜坡函数r(t)=t，其拉氏变换为则输出的拉氏变换为2s1sR/)(195显然，系统的响应从t=0时开始跟踪输入信号而单调上升，在达到稳态后，它与输入信号同速增长，但它们之间存在跟随误差。即且可见，当t趋于无穷大时，误差趋近于T，因此系统在进入稳态以后，在任一时刻，输出量c(t)将小于输入量r(t)一个T值，时间常数T越小，系统跟踪斜坡输入信号的稳态误差也越小。)1()()()(TteTtctrteTtet)(lim稳态误差ess=T，初始斜率=0，稳态输出斜率=1.196系统的单位脉冲响应就是系统闭环传递函数的拉氏反变换T1sT11Ts1SC)(3.2.33.2.3单位脉冲响应单位脉冲响应设系统的输入为单位脉冲函数r(t)=δ(t),其拉氏变换为R(s)=1,则输出响应的拉氏变换为TteTtC1)(（（t≥0t≥0））对上式进行拉氏反变换，求得单位脉冲响应为0.3680.368C(t)C(t)3T3TT1T1斜率斜率21TC(t)C(t)TT2T2Ttt一阶系统的脉冲响应一阶系统的脉冲响应响应曲线如图所示。197输入r(t)=(t)，输出)()(0teT1tctT1t0.135/T0.018/TT2T3T4T初始斜率为0.368/T0.05/T0t/TeT1c(t)T1g(t)(c)单位脉冲响应曲线2T1特点：1)可以用时间常数去度量系统的输出量的数值；2)初始斜率为-1/T2；3)无超调；稳态误差ess=0。198按照脉冲函数，阶跃函数、斜坡函数的顺序，前者是后者的导数，而后者是前者的积分。脉冲响应、阶跃响应、斜坡响应之间也存在同样的对应关系。表明：0.368C(t)3TT1T1斜率21TC(t)T2Ttt一阶系统的脉冲响应线性定常系统的一个重要特征系统对某种输入信号导数的响应，等于对该输入信号响应的导数；对某种输入信号积分的响应，等于系统对该输入信号响应的积分。21TT1单位脉冲响应是单调下降的指数曲线，曲线的初始斜率为，输出量的初始值为。不存在稳态分量.1993.2.4一阶系统的单位加速度(抛物线）响应跟踪误差：e(t)=r(t)-c(t)=Tt-T2(1-e-t/T)随时间推移而增长，直至无穷。因此一阶系统不能跟踪加速度函数。221)(ttr输入)1(21)(/22TteTTtttc输出结论：•一阶系统的典型响应与时间常数T密切相关。只要时间常数T小，单位阶跃响应调节时间小，单位斜坡响应稳态值滞后时间也小。但一阶系统不能跟踪加速度函数。•线性系统对输入信号导数的响应，等于系统对输入信号响应的导数。200Tte1tC)()0(t)(1)(ttrTteT1tC)(（（t≥0t≥0））)()(ttr)1()(TtTteTtTeTttC（（t≥t≥00））ttr)(不仅适用于一阶线性定常系统，也适用于高阶线性定常系统。201解:(1)与标准形式对比得：T=1/10=0.1,ts=3T=0.3s例3.1某一阶系统如图,在单位阶跃信号作用下（1）若Kh=0.1求调节时间ts,（2）若要求ts=0.1s,求反馈系数Kh.10/110101001.0)/100(1/100)()(1)()(sssssHsGsGs(2)要求ts=0.1s，即3T=0.1s,即,得hhhKsKsKss100/1/1/1001/100)(310K1001h.30Kh.0.1C(s)R(s)E(s)100/s(-)解题关键：化闭环传递函数为标准形式。Kh2023.3二阶系统的时域响应由二阶微分方程描述的系统称为二阶系统。在控制工程实践中，二阶系统应用极为广泛，此外，许多高阶系统在一定的条件下可以近似为二阶系统来研究，因此，讨论和分析二阶系统的特征具有重要的实际意义。KsTsKsRsCs2)()()()1(TssKR(t)R(t)__C(t)C(t)二阶系统结构图二阶系统结构图设二阶系统的结构图如图所示。系统的闭环传递函数为其中K为系统的开环放大系数，T为时间常数。203式中，称为无阻尼自然振荡角频率，（简称为无阻尼自振频率），称为阻尼系数（或阻尼比）。TKn2222)()()(nnnsssRsCs为了分析方便，将系统的传递函数改写成如下形式它的两个根为二阶系统特征根（即闭环极点）的形式随着阻尼比取值的不同而不同。1Ps2nn2121,,0222nnss系统的闭环特征方程为TK212043.3.1二阶系统的单位阶跃响应设系统的输入为单位阶跃函数，则系统输出响应的拉氏变换表达式为对上式取拉氏反变换，即可求得二阶系统的单位阶跃响应。ssssRssCnnn1.2)()()(222（一）过阻尼（>1）的情况系统具有两个不相等的负实数极点121nnP122nnPjj1P2P00[s][s]1过阻尼时极点分布20522110212))(()(pspsspspsssCn1])([00sssC121112)]()([1ppssCnps222212)]()([2ppssCnpsC(t)C(t)ttoo11过阻尼响应过阻尼响应)(121)(21221pepetCtptpn)0(t稳态分量为1，瞬态分量包含两个衰减指数项，曲线单调上升。分析：当时，极点比距虚轴远得多，故比衰减快的多，可将二阶系统近似成一阶系统来处理。12p1ptpe2tpe11阻尼比>1时二阶系统的运动状态为过阻尼状态。系统的单位跃响应无振荡、无超调、无稳态误差.206))(()(2dndnnjsjsssC22210)(dnsss1P2P21njnn[s][s]oo10欠阻尼时的极点分布211nnjp221nnjp(二)欠阻尼（）的情况系统具有一对在S平面的左半部的共轭复数极点，10式中，称为阻尼自振频率21nd11n22102222)()(1)(dnddndnnsssssC207])([£221-dnnss])([£221-dnds)sin1(cos1)(2ttetCddtn)sincos1(1122tteddtntedtncostedtnsin21sincos1P2P21njnn[s][s]oo10欠阻尼时的极点分布欠阻尼时的极点分布0)sin(11)(2ttetCdtn21arctgarccos208系统的稳态响应为1，瞬态分量是一个随时间t的增大而衰减的正弦振荡过程。振荡的角频率为，它取决于阻尼比和无阻尼自然频率。衰减速度取决于的大小。此时系统工作在欠阻尼状态。输出响应如图所示。ttC(t)C(t)1100欠阻尼响应欠阻尼响应ndn0)sin(11)(2ttetCdtn209稳态部分等于1，表明不存在稳态误差；瞬态部分是阻尼正弦振荡过程，阻尼的大小由n(即特征根实部）决定；振荡角频率为阻尼振荡角频率d（特征根虚部），其值由阻尼比ζ和自然振荡角频率n决定。欠阻尼二阶系统的单位阶跃响应由稳态稳态和瞬态瞬态两部分组成：210（三）临界阻尼（）的情况系统具有两个相等的负实数极点，1np2,121PPnjoo[s][s]1临界阻尼时极点的分布1])([00sssC1]))(([{21nsnssCdsdnsnnssC])()([22221022)()()(nnnnssssssCtntnnteetC1)()1(1tentn)0(ttt11ooC(t)C(t)临界阻尼响应系统的输出响应无超调、无振荡,由零开始单调上升，最后达到稳态值1，不存在稳态误差。是输出响应的单调和振荡过程的分界，通常称为临界阻尼状态。1211系统有一对共轭纯虚数极点,它们在S平面上的位置如图所示。njp2,1ttCncos1)(0（四）无阻尼（）的情况jn1P2P[s][s]oo0(a)(a)无阻尼时的极点分布和响应C(t)(b)1to系统的输出响应是无阻尼的等幅振荡过程，其振荡频率为n)sin1(cos1)(2ttetCddtn0将代入212输出响应是发散的，此时系统已无法正常工作。n——无阻尼自然振荡频率，此时系统输出为等幅振荡d————阻尼振荡频率。系统输出为衰减正弦振荡过程。阻尼振荡频率。系统输出为衰减正弦振荡过程。综上所述，不难看出频率和的物理意义。nd根据上面的分析可知，在不同的阻尼比时，二阶系统的响应具有不同的特点。因此阻尼比是二阶系统的重要特征参数。分析0121nnP122nnP系统具有实部为正的极点，若选取为横坐标，可作出不同阻尼比时二阶系统单位阶跃响应曲线。tn213系统无振荡时，以临界阻尼时过渡过程的时间最短，此时，系统具有最快的响应速度。系统在欠阻尼状态时，若阻尼比在0.4～0.8之间，则系统的过渡过程时间比临界阻尼时更短，此时振荡特性也并不严重。如图所示，此时曲线只和阻尼比有关。8.0~4.0一般希望二阶系统工作在的欠阻尼状态下，通常选取作为设计系统的依据。21)(tC03.01.05.07.012tn二阶系统的阶跃响应越小，响应特性振荡得越厉害,随着增大到一定程度，响应特性变成单调上升的。214在实际应用中，控制系统性能的好坏是通过系统的单位阶跃响应的特征量来表示的。为了定量地评价二阶系统的控制质量，必须进一步分析和对系统单位阶跃响应的影响，并定义二阶系统单位阶跃响应的一些特征量作为评价系统的性能指标。n3.3.2．二阶系统瞬态性能指标此时，系统在具有适度振荡特性的情况下，能有较短的过渡过程时间，因此下面有关性能指标的定义和定量关系的推导，主要是针对二阶系统的欠阻尼工作状态进行的。控制系统的单位阶跃响应一般与初始条件有关，为了便于比较各种系统的控制质量，通常假设系统的初始条件为零。8.0~4.0除了一些不允许产生振荡的系统外，通常希望二阶系统工作在的欠阻尼状态下。215动态性能当系统受到外部扰动的影响或者参考输入发生变化时，被控量会随之发生变化，经过一段时间，被控量恢复到原来的平衡状态或到达一个新的给定状态，称这一过程为过渡过程在时域中，常用单位阶跃信号作用下，系统输出的超调量p,上升时间Tr，峰值时间Tp,过渡过程时间（或调整时间）Ts和振荡次数N等特征量表示。216系统在欠阻尼情况下的单位阶跃响应为)sin(11)(2tetCdtn)0(t对应的响应曲线如图所示。由上式和图所示曲线来定义系统的瞬态性能指标，同时讨论性能指标与特征量之间的关系。超调量C(t)C(t)上升时间tr峰值时间tp调节时间ts误差带误差带稳态误差稳态误差)(too1.01.0tt控制系统性能指标控制系统性能指标217(一)上升时间响应曲线从零开始上升，第一次到达稳态值所需的时间，称为上升时间。rt21rnte0)sin(rdtrtt1)(rtC根据上述定义，当，，由式可得)sin(11)(2tetCdtn)0(t0)sin(rdtktrd21ndrt（k=0,1,2……）当一定时，阻尼比越大，上升时间越长，nrtnrt当一定时，越小，越长。218tp（二）峰值时间（二）峰值时间响应曲线响应曲线CC（（tt）从零开始到达第一个峰值所需时间，称为峰值时）从零开始到达第一个峰值所需时间，称为峰值时间。间。0)(pttdttdC)sin(pdnt0)cos(pddt)(pdttgnd21tg由定义，令得ktpdktpd所以即（k=1,2，……）分析、与的关系。nptpt21ndpt因为峰值时间是C(t)到达第一个峰值的时间，故取k=1,219可见，当一定时，越大，越小，反应速度越快。当一定时，越小，越大。由于是闭环极点虚部的数值，越大，则闭环极点到实轴的距离越远，因此，也可以说峰值时间与闭环极点到实轴的距离成反比。nptnptddpt分析、与的关系。nptpt21ndpt因为峰值时间是C(t)到达第一个峰值的时间，故取k=1,220p（三）超调量在响应过程中，输出量C（t）超出其稳态值的最大差量与稳态值之比称为超调量。根据超调量的定义，并考虑到1)(C%100%100)()()(21eCCtCpp2111)(2etCp)sin(21sin)sin(输出量的最大值为211)(etCp所以%100)()()(CCtCpp)(ptC)(C超调量可表示为式中为输出量的最大值，为输出量的稳态值。221上式表明，只是的函数，与无关，越小,则越大。当二阶系统的阻尼比确定后，即可求得对应的超调量。反之，如果给出了超调量的要求值，也可求得相应的阻尼比的数值。一般当时，相应的超调量为pnpp8.0~4.0%5.1~25p%100%100)()()(21eCCtCppp100100909080807070606050504040303020201010000.20.20.40.40.60.60.80.81.01.0欠阻尼二阶系统超调与阻尼比关系曲线p与的关系曲线如图所示。222)sin(12tedtn)(stt（四）调节时间st%5%2响应曲线到达并停留在稳态值的（或)误差范围内所需的最小时间称为调节时间（或过渡过程时间）。)()()(CCtC)(stt由定义下式成立1)(C05.0式中（或0.02）21tne)(stt采用近似的计算方法，忽略正弦函数的影响，认为指数项衰减到0.05（或0.02）时，过渡过程即进行完毕，得到1td)sin(22305.0nst211ln302.0nst211ln4在时，上面两式可分别近似为和9.00nst3nst4可以近似认为调节时间与闭环极点到虚轴的距离成反比。在设计系统时，通常由要求的超调量所决定，而调节时间则由自然振荡频率所决定。即在不改变超调量的条件下，通过改变的值可以改变调节时间。stnn)11ln1(ln111ln122nnst由此可求得224dsTtNnst3215.1N05.002.0nst4212N（五）振荡次数Nst响应曲线在0～时间内波动的次数称为振荡次数。ddT2式中称为系统的阻尼振荡周期。振荡次数只与阻尼比有关。st225作业p71.3-8(1)P72.3-12226阻尼比和无阻尼自振频率是二阶系统两个重要特征参数，它们对系统的性能具有决定性的影响。nnpst)8.00(rtpt当保持不变时，增大可使和下降,但使和上升，显然在系统的振荡性能和快速性之间是存在矛盾的。当保持不变时，提高可使、、下降，从而提高系统的快速性，同时保持和N不变。nrtptstpn要使二阶系统具有满意的动态性能，必须选取合适的阻尼比和无阻尼自振荡率。通常可根据系统对超调量的限制要求选定，然后在根据其它要求来确定22712n102n158.016.3nR(s)R(s)E(s)E(s)--)1(10ssC(s)C(s)(a)(a)(b)(b)R(s)R(s)E(s)E(s)C(s)C(s)----)1(10sssKt例例3.23.2系统结构图系统结构图55.011221nrtgt（秒）（秒）1010)(2sss解系统（a）的闭环传递函数为例3.2设控制系统如图所示。其中（a）为无速度反馈系统，（b）为带速度反馈系统，试确定是系统阻尼比为0.5时的值，并比较系统（a）和(b)阶跃响应的瞬态性能指标。01.112npt（秒）（秒）%4.60%10021ep63nst（秒）（秒）)05.0(315.12N（次）（次）)05.0(tK228tnK1012102n1012ntK216.010116.35.021016.310)(2sss系统（b）的闭环传递函数为结论：采用速度反馈后，可以明显地改善系统的动态性能。10)101(10)(2sKsst%3.16p183.0N7.0rt（秒）（秒）15.1pt（秒）（秒）9.1st（秒）（秒）5.016.3n由和可求得5.0将代入，解得229KnKaan22)()(assKsG%10p2%)5(st例3.3设单位反馈系统的开环传递函数为若要求系统的阶跃响应的瞬态性能指标为试确定参数K和a的值。KassKs2)(解系统的闭环传递函数为%10%10021ep3.21.0ln1259.023nst（秒）（秒）54.2n32na46.6K230若描述系统的微分方程高于二阶，则该系统为高阶系统。控制工程中，大多数控制系统都是高阶系统。理论上，高阶系统也可以直接由传递函数求出它的时域响应，然后按上述二阶系统的分析方法来确定系统的瞬态性能指标。但是，高阶系统的分布计算比较困难，同时，在工程设计的许多问题中，过分讲究精确往往是不必要的，甚至是无意义的。因此，工程上通常把高阶系统适当地简化成低阶系统进行分析。2313.43.4控制系统的稳定性控制系统的稳定性在控制系统的分析研究中，最重要的问题是系统的稳定性问题。不稳定的系统在受到外界或内部的一些因素扰动时，会使被控制量偏离原来的平衡工作状态，并随时间的推移而发散。因此，不稳定的系统是无法正常工作的。在这一节中将讨论稳定性的定义，稳定的充要条件及判别稳定性的基本方法。3.4.13.4.1稳定的概念和定义稳定的概念和定义在自动控制理论中，有多种稳定性的定义，这里只讨论其中最常用的一种，即渐近稳定性的定义。232稳定与不稳定系统的示例'AAf图aAf图b图cdfcA图c中，小球在C、D范围内，系统是稳定的，故可以认为该系统是条件稳定系统。图a为稳定的系统。图b为不稳定系统。2333.4.23.4.2稳定的充要条件稳定的充要条件稳定性是系统在扰动消失后，自身具有的一种恢复能力，它是系统的一种固有特性，这种特性只取决于系统的结构和参数，与外作用无关。线性定常系统的稳定性的定义：如果线性定常系统受到扰动的作用，偏离了原来的平衡状态，而当扰动消失后，系统又能够逐渐恢复到原来的平衡状态，则称该系统是渐近稳定的（简称为稳定）。否则，称该系统是不稳定的。234设线性定常系统在初始条件为零时，输入一个理想单位脉冲，这相当于系统在零平衡状态下，受到一个扰动信号的作用，如果当t趋于时，系统的输出响应C(t)收敛到原来的零平衡状态，即该系统就是稳定的。0)(limtCt011011......)(asasabsbsbsnnnnmmmm)(t)(t根据上述稳定性的定义，可以用函数作为扰动来讨论系统的稳定性。根据这一思路分析系统稳定的充要条件。设系统的闭环传递函数为235特征方程为如果特征方程的所有根互不相同，且有q个实数根和r对共轭复数根,则在单位脉冲函数的作用下，系统输出量的拉氏变换可表示为将上式用部分分式法展开并进行拉氏反变换得式中0...011asasannnni21nknkkj)(t1)2()()()(11221qirknknkkimjjrsspszsKsCqirkdkkdkkttitCteetCnkki11)sincos()(21nkdk236上式表明当系统特征方程的根都具有负实部时，则各瞬态分量都是衰减的，且有，此时系统是稳定的。0)(limtCt线性定常系统稳定的充分必要条件：闭环系统特征方程的所有根都具有负实部，即闭环传递函数的所有极点均位于为S平面的左半部分（不包括虚轴）。如果特征根中具有一个或一个以上的零实部根，而其余的特征根均有负实部，则C（t）趋于常数或作等幅振荡，这时系统处于稳定和不稳定的临界状态，称为临界稳定状态。对于大多数实际系统，当它处于临界状态时，也是不能正常工作的，所以临界稳定的系统在工程上属于不稳定系统。)(limtCt如果特征根中有一个或一个以上具有正实部，则该根对应的瞬态分量是发散的，此时有，系统是不稳定的。2373.4.33.4.3劳斯稳定判据劳斯稳定判据控制系统的稳定的充要条件是其特征方程的根均具有负实部。因此，为了判别系统的稳定性，就要求出系统特征方程的根，并检验它们是否都具有负实部。但是，这种求解系统特征方程的方法，对低阶系统尚可以进行，而对高阶系统，将会遇到较大的困难。因此，人们希望寻求一种不需要求解的特征方程就能判别系统稳定性的间接方法，劳斯判据就是其中的一种。劳斯判据利用特征方程的各项系数进行代数运算，得出全部特征根具有负实部的条件，以此作为判别系统是否稳定的依据。因此，这种判据又称为代数稳定判据。2381、稳定的必要条件设系统的特征方程为式中（当时，可将方程两边同乘以-1）。若该方程的特征根为（1,2,….n）,该n个根可以是实数也可以是复数，则上式可改写成为将上式展开0......0111asasasannnn0na0naip0))......()((......210111nnnnnnnpspspsaasaasaas)......(211nnnaannnnaa1423231212............nnnaa......)1(210…………239由此可见，如果特征方程的根都具有负实部，则上式的所有系数必然都大于零。故系统稳定的必要条件是其特征方程的各项系数均为正，即naaa,,,10),,2,1,0(0niainppp,,21根据必要条件，在判别系统的稳定性时，可事先检查系统特征方程的系数是否都大于零，若有任何系数是负数或等于零，则系统是不稳定的。但是，当特征方程满足稳定的必要条件时，并不意味着系统一定是稳定的，为了进一步确定系统的稳定性，可以使用劳斯判据。2402.劳斯判据应用劳斯判据分析系统的稳定性时，可按下述方法进行。将系统的特征方程写成如下标准形式1d0......0111asasasannnn)0(0a将方程各项系数组成劳斯表将方程各项系数组成劳斯表……nsna2na6na4na1ns7na5na3na1na2ns1b4b3b2b………………3ns1c4c3c2c………………4ns2s1e2e1s1f0s1g………………………………………………2d3d4d241计算劳斯表的各系数13211nnnnnaaaaab15412nnnnnaaaaab17613nnnnnaaaaabib……系数的计算一直进行到其余的b值全部等于零为止。用同样的前两行系数交叉相乘的方法，可以计算c,d,……e,f,g各行的系数。242这个计算过程一直进行到n+1行为止。为了简化运算，可以用一个正整数去乘或除其一行的各项，不改变稳定性的结论。121211)(ccbbcd131312)(ccbbcd……………………131512bbaabcnn141713bbaabcnn121311bbaabcnn……………………243劳斯稳定判据（1）劳斯表第一列所有系数均不为零的情况如果劳斯表中第一列的系数都具有相同的符号，则系统是稳定的，否则系统是不稳定的。且不稳定根的个数等于劳斯表中第一列系数符号改变的次数。2443s6676171146658621106677916676586176672s26670626671s7916150677912667658677910s22例3.5已知系统的特征方程为已知系统的特征方程为试用劳斯判据分析系统的稳定性。试用劳斯判据分析系统的稳定性。0210171462345sssss解列劳斯表5s4s114106172245劳斯表第一列的系数符号相同，故系统的是稳定的。由于判别系统是否稳定只与劳斯表中第一列系数的符号有关，而把劳斯表中某一行系数同乘以一个正数不会改变第一列系数的符号，所以为简化运算，常把劳斯表的某一行同乘以一个正数后，再继续运算。本例中，劳斯表可按如下方法计算：1141061726758(同乘以6)791134（同乘以67）36900（同乘以791）134由于第一列系数的符号相同，故系统稳定，结论与前面一致。5s4s3s0s1s2s246例3.6已知系统的特征方程为s4+2s3+s2+s+1=0试用劳斯判据判断系统的稳定性。解列劳斯表如下S4111S3210S2(21－11)/2=1/2(21－10)/2=1S1(11－22)/1=－3S0(－32－10)/－3=2由于劳斯表第一列的系数变号两次，一次由1/2变为-3，另一次由-3变为2，故特征方程有两个根在S平面右半部分，系统是不稳定的。247(2)劳斯表某行的第一列系数等于零，而其余各项不全为零的情况当劳斯表某一行的第一列系数为零，而其余项不全为零，可用一个很小的正数代替第一列的零项，然后按照通常方法计算劳斯表中的其余项。248例3.7已知系统的特征方程为试判别系统的稳定性.解：由特征方程列出劳斯表125120554s1s3s0s2s00522234ssss5252当的取值足够小时，将取负值，故劳斯表第一列系数变号两次，由劳斯判据可知，特征方程有两个根具有正实部，系统是不稳定的。对于这种情况，也可以用(s+1)因子乘以原特征方程，然后按新的特征方程计算劳斯表。例如在上例中用(s+1)乘以原特征方程得249劳斯表为13724529（同乘以2）-10101110显然，劳斯表第一列系数变号两次，其结论与前面是一致的。057432)1)(522(2345234ssssssssss5s0s1s2s3s4s250例如，，等等。显然，系统是不稳定的。此时，为了确定根的分布情况，可按下列步骤处理：jj(3)劳斯表某行所有系数均为零的情况如果劳斯表中某一行（如第k行）各项为零，这说明在S平面内存在以原点为对称的特征根。利用第k-1行的系数构成辅助方程。求辅助方程对s的导数，将其系数代替原全部为零的k行，继续计算劳斯表。特征方程中以原点为对称的根可由辅助方程求得。2511820162121621216000由上表看出，行的各项全为零，为了求出～各行，由行的各项系数构成辅助方程将辅助方程对s求导得用上式各项系数作为行的各系数继续计算劳斯表得6s3s4s5s3s4s016122)(24sss3s0s0s24s8dssd3)(3s例3.8已知系统的特征方程为分析系统的稳定性。。0161620128223456ssssss解由特征方程列劳斯表解由特征方程列劳斯表25218201621216212168246168/3166s1s2s3s4s5s0s3s01612224ss由于劳斯表第一列系数符号都相同，因此，可以确定没有特征方程根分布在S平面的右半部分。但由于行的各项均为零，这表明系统有共轭虚根，所以系统是不稳定的，共轭虚根可由辅助方程求得，即由1,22sj24,3js253综上所述，应用劳斯表判据分析系统的稳定性时，一般可以按如下顺序进行：1、确定系统是否满足稳定的必要条件。当特征方程的系数不满足(i=0,1,2,……n)时，系统是不稳定的。2、当特征方程的系数满足(i=0,1,2,……n)时，计算劳斯表。当劳斯表的第一列系数都大于零时，系统是稳定的。如果第一列出现小于零的系数，则系统是不稳定的。3、若计算劳斯表时出现情况（2）和（3），此时为确定系统极点的分布情况，可按情况（2）和（3）的方法处理。0ia0ia运用劳斯判据，不仅可以判定系统是否稳定，还可以用来分析系统参数的变化对稳定性产生的影响，从而给出使系统稳定的参数范围。2542.06.86n例3.9已知系统的结构图如图所示。当时,试确定k为何值时，系统稳定。R(s)-E(s)1+C(s)sK)2(nnss2)2()()(22nnsskssG222322)()(nnnnKssskss解开环传递函数为其闭环传递函数为255特征方程为将，代入特征方程得由特征方程列劳斯表1750034.67500K7500K022223nnnKsss2.06.86n0750075006.3423Ksss6.3475007500346K3s2s1s0s07500K06.34750075006.34K要使系统稳定，必须满足解不等式得6.34,0KK参数K的取值范围是6.340K256应用劳斯判据可检验系统是否有一定的稳定裕度，即相对稳定性。令即把虚轴左移。将上式代入系统的特征方程式，得到以z为变量的新特征方程式，然后用劳斯判据检验新特征方程式有没有根位于新虚轴的右边。如果所有根均在新虚轴的左边，则说明系统具有稳定裕量。1zs257例3.10检验特征方程式是否有根在右半平面，并检验有几个根在直线s=-１的右边。023413102sss解劳斯阵列表为s3213s2104s112.2s04第一列无符号改变，故没有根在S右半平面。令s=z-1，代入特征方程式，得即04)1()1()1(23zzz1310201423zzz2z32-1z24-1z1-1/2z0-1第一列符号改变一次，故有一个根在直线s=-1(即新座标虚轴)的右边，因此稳定裕量不到1。[s][z]zs00258作业P703-3(1)P713-5259应用劳斯表判据分析系统的稳定性时，一般可以按如下顺序进行：1、确定系统是否满足稳定的必要条件。当特征方程的系数不满足(i=0,1,2,……n)时，系统是不稳定的。2、当特征方程的系数满足(i=0,1,2,……n)时，计算劳斯表。当劳斯表的第一列系数都大于零时，系统是稳定的。如果第一列出现小于零的系数，则系统是不稳定的。3、若计算劳斯表时出现情况（2）和（3），此时为确定系统极点的分布情况，可按情况（2）和（3）的方法处理。0ia0ia线性定常系统稳定的充分必要条件：闭环系统特征方程的所有根都具有负实部，即闭环传递函数的所有极点均位于为S平面的左半部分（不包括虚轴）。260在系统的分析中，劳斯判据可以根据系统特征方程的系数来确定系统的稳定性，同时还能给出系统的某些参数的取值范围。但是，它的应用也具有一定的局限性，通常它只能提供系统绝对稳定性的结论，而不能指出系统是否具有满意的动态过程。此外，当系统不稳定时，它不能提供改善系统稳定性的方法和途径。2613.5控制系统的稳态性能分析系统的稳态性能反映系统跟踪控制信号的准确度或抑制扰动信号的能力，这种能力用稳态误差来描述。在系统的分析、设计中，稳态误差是一项重要的性能指标，它与系统本身的结构、参数及外作用的形成有关，也与元件的不灵敏、零点漂移、老化及各种传动机械的间隙、摩擦等因素有关。本节只讨论由于系统结构、参数及外作用等因素所引起的稳态误差。给定值稳态误差（由给定输入引起的稳态误差）扰动值稳态误差（由扰动输入引起的稳态误差）对于随动系统，给定输入变化，要求系统输出量以一定的精度跟随输入量的变化，因而用给定稳态误差来衡量系统的稳态性能。对恒值系统，给定输入通常是不变的，需要分析输出量在扰动作用下所受到的影响，因而用扰动稳态误差来衡量系统的稳态性能。本章介绍稳态误差的概念和计算方法，研究稳态误差的规律性。2623.5.13.5.1稳态误差的定义稳态误差的定义系统的误差e(t)一般定义为输出量的希望值与实际值之差。对图示典型系统，其误差定义有两种形式：R(s)-B(s)N(s)+C(s))(1sG)(2sG)(sH反馈系统结构图)()()(tCtCter)(tCr（1）从系统输出端定义式中，为系统输出量的希望值，C(t)为输出量的实际值。（2）从输入端定义系统输出量的希望值是给定输入r(t)，输出量的实际值为系统主反馈信号b(t)。通常H（s）是测量装置的传递函数，此时误差是给定输入与测量装置输出量之差。b(t)可以测量，因而具有实用性。)()()(tbtrte263第一种形式的误差是从系统输出端来定义的，它在性能指标提法中经常使用，但在实际系统中无法测量，因而，一般只有数学意义。而第二种形式的误差是从系统的输入端来定义的，它在系统中是可以测量的，因而具有实用性。对于单位反馈系统，要求输出量C(t)的变化规律与给定输入r(t)的变化规律完全一致，所以给定输入r(t)也就是输出量的希望值，即。此时，上述两种定义统一为e(t)=r(t)-c(t))(tCr)()(trtCrR(t)-B(s)E(s)N(s)+C(s))(1sG)(2sG)(sH反馈系统结构图264从本质上看，两种定义的误差都能反映控制系统的控制精度。在下面的讨论中，采用第二种误差定义。e(t)通常也称为系统的误差响应，它反映了系统在输入信号和扰动信号作用下整个工作过程中的精度。误差响应中也包含有瞬态分量和稳态分量两个部分，如果所研究的系统是稳定的，那么当时间t趋于无穷大时，瞬态分量趋近于零，剩下的只是稳态分量。)(limteetsssse稳态误差的定义：稳定系统误差信号的稳态分量称为系统的稳态误差，以表示。2653.5.23.5.2输入作用下的稳态误差输入作用下的稳态误差如果不计扰动输入的影响，可求得系统的给定稳态误差。此时，系统的结构图为E(s)R(s)B(s)G(s)H(s)C(s)--)()()(1)()(sRsHsGsGsC)()()()()()(sCsHsRsBsRsE由误差的定义可知)()()()()(11sRssRsHsGer)()(11)(sHsGser称为给定输入作用下系统的误差传递函数。266设系统的开环的传递函数为)1()1()1()1)(1()1()1)(1()()(112211niimjjnmsssKsTsTsTssssKsHsGs分母中的表示开环传递函数在原点处有重极点，或者说有个积分环节串联。)()(lim0sHsGsKs式中称为系统的开环放大环节或开环增益。267它表明，在给定输入作用下，系统的稳态误差与系统的结构、参数和输入信号的形式有关(系统的稳态误差取决于原点处开环极点的阶次、开环增益K以及输入信号的形式).对于一个给定的系统，当给定输入的形式确定后，系统的稳态误差将取决于以开环传递函数描述的系统结构.给定稳态误差的基本公式为(终值定理)为了分析稳态误差与系统结构的关系，可以根据开环传递函数G(s)H(s)中串联的积分环节来规定控制系统的类型。)(limteetss)(lim0ssEs)()(1)(lim0sHsGssRssKsRssKsTsssRsTsssnimjjiniis0101110lim)]([lim)1()1()()1(lim（G(s)H(s)的时间常数形式）268设系统的开环的传递函数为)1()1()1()1)(1()1()1)(1()()(112211niimjjnmsssKsTsTsTssssKsHsGs210,,分母中的表示开环传递函数在原点处有重极点，或者说有个积分环节串联。当……时，分别称系统为0型、1型、2型……系统。分类是以开环传递函数中串联的积分环节数目为依据的，而C(s)H(s)中其它零、极点对分类没有影响。下面分析系统在不同典型输入信号作用下的稳态误差。)()(lim0sHsGsKs式中称为系统的开环放大环节或开环增益。269)()(lim111)()(100limsHsGssHsGsessss1、单位阶跃输入时的稳态误差对于单位阶跃输入，对于单位阶跃输入，R(s)=1/s,R(s)=1/s,求得系统的稳态求得系统的稳态误差为误差为)()(lim0sHsGKsppK令称为稳态位置误差系数。pssKe11稳态误差可表示为0KssKKniimjjsp110)1()1(lim因此，在单位阶跃输入下，给定稳态误差决定于系统的位置误差系数。对于0型系统，270对实际系统来说，通常是允许存在稳态误差的，但不允许超过规定的指标。为了降低稳态误差，可在稳定条件允许的前提下，增大系统的开环放大系数，若要求系统对阶跃输入的稳态误差为零，则必须选用1型或高于1型的系统。011pssKeniimjjspsssKK110)1()1(lim1对于1型系统（或高于1型的系统），sse由于0型系统中没有积分环节，它对阶跃输入的稳态误差为一定值，误差的大小与系统的开环放大系数K成反比，K越大，越小，只要K不是无穷大，系统总有误差存在。2712、单位斜坡输入时的稳态误差对于单位斜坡输入，此时系统的稳态误差为21)(ssR)()(lim11)()(1lim020sHssGssHsGsessss)()(lim0sHssGKsv令称为稳态速度误差系数。vssKe1于是稳态误差可表示为因此，在单位斜坡输入下，给定稳态误差决定于速度误差系数。2720)1()1(lim110niimjjsvssKsK对于0型系统，0vssKe1KsssKsKniimjjsv1110)1()1(limKKevss111对于1型系统，273对于2型系统（或高于2型的系统）niimjjsvsssKsK)1()1(10lim01vssKe1计算表明，在单位斜坡输入作用下，0型系统的稳态误差为，而1型系统的稳态误差为一定值，且误差与开环放大系数成反比。为了使稳态误差不超过规定值，可以增大系统的K值。2型或高于2型系统的稳态误差总为零。因此，对于单位斜坡输入，要使系统的稳态误差为一定值或为零，必需，也即系统必须有足够积分环节。2743、单位抛物线输入时的稳态误差对于单位抛物线输入，此时系统的稳态误差为31)(ssR)()(lim11)()(12030limsHsGsssHsGsessss)()(lim20sHsGsKsa令assKe1aK称为稳态加速度误差系数。稳态误差可表示为0)1()1(1120limniimjjsassKsK对于0型系统，assKe1稳态误差可表示为2750)1s(s)1s(KsKn1iim1jj20salimassKe11对于1型系统，K)1s(s)1s(KsK2n1ii2m1jj20salimKKeass112对于2型系统，276对于3型系统（或高于3型的系统），3niimjjsasssKsK1120)1()1(lim01assKe以上计算表明，在单位抛物线输入作用下，0型和1型系统的稳态误差为,2型系统的稳态误差为一定值，且误差与开环放大系数成反比。对3型或高于3型的系统，其稳态误差为零。但是，此时要使系统稳定则比较困难。277在各种典型输入信号作用下，不同类型系统的给定稳态误差如下表所示。输入信号作用下系统的稳态误差III系统类别静态误差系数阶跃输入)()(tIRtr斜坡输入r(t)=Rt加速度输入2)(2RttrIIIpKaKK0pssK1ReKR1KRessassKReKRKRK000000000KK278若给定的输入信号不是单位信号时，则将系统对单位信号的稳态误差成比例的增大，就可以得到相应的稳态误差。若给定输入信号是上述典型信号的线性组合，则系统相应的稳态误差可由叠加原理求出。aKpKvK综上，稳态误差系数、、和描述了系统对减小和消除稳态误差的能力，可表示系统的稳态特性。提高开环放大系数K或增加开环传递函数中的积分环节数，都可以达到减小或消除系统稳态误差的目的。但是，这两种方法都受到系统稳定性的限制。因此，对于系统的准确性和稳定性必须统筹兼顾、全面衡量。avpssKCKBKe1则系统的总稳态误差为221)(Ctttr例如，若输入信号为279例3.11设图示系统的输入信号r(t)=10+5t，分析系统的稳定性并求出其稳态误差。R(s)-C(s))12)(1()15.0(ssssk例3.11系统结构图22)(sssR332)(sCsssR1ssR)(由以上讨论可知，当时，系统相对的稳态误差为零，当时，系统相对的稳态误差为零；当时，系统相对的稳态误差为零。因此，当开环系统含有个串联积分环节时，称系统对给定输入r(t)是阶无差系统，而称为系统的无差度。2800Ks)K5.01(s3s223解由图求得系统的特征方程为3s0s1s2s32)5.01(3KK23K5.01KK要使系统稳定，必须0K05.01K02)5.01(3KK6,2,0KKK解得60K所以，当，系统是稳定的。281上述结果表明，系统的稳态误差与K成反比，K值越大，稳态误差越小，但K值的增大受到稳定性的限制，当K>6时，系统将不稳定。KssssKsssGKssv)12)(1()15.0()(limlim00)12)(1()15.0()(limlim00ssssKsGKssp系统的稳态误差系数分别为由图可知，系统的开环传递函数为)12)(1()15.0()(ssssKsGKKKevpss55110所以，系统的稳态误差为282)()()()(1)()(212sNsHsGsGsGsC)()()()()()(1)()()(212sNssNsHsGsGsHsGsEen3.5.33.5.3扰动稳态误差扰动稳态误差—扰动输入作用下系统的误差传递函数)()()(1)()()(212sHsGsGsHsGsen2012()()()()1()()()limlimsstssGsHseetNsGsGsHs控制系统除了受到给定输入的作用外，通常还受到扰动输入的作用。扰动稳态误差的大小，反映了系统的抗干扰能力。扰动输入可以作用在系统的不同位置，因此系统对于某种形式的给定输入的稳态误差为零，但对同一形式的扰动输入其稳态误差则不一定为零。)()()()()(sCsHsBsRsER(s)-B(s)N(s)+C(s))(1sG)(2sG)(sHE(s)设给定输入为零，由误差信号的定义可得扰动输入引起的误差为283例3.12设控制系统如图所示，其中给定输入，扰动输入（和均为常数），试求系统的稳态误差。sKsG1111)()1()(222ssKsG)(1)(tRtrr)(1)(tRtnnrRnR解当系统同时受到给定输入和扰动输入的作用时，其稳定误差为给定稳态误差和扰动稳态误差的叠加。令n(t)=0时，求得给定输入作用下的误差传递函数为)s(G)s(G11)s(21erR(s)-)(1sG)(2sG+N(s)C(s)所以给定稳态误差为0sRKK)s1)(s1(s)s1)(s1(s)s(G)s(G1)s(Rser21212120s210sssrlimlim284)()(1)()(212sGsGsGsen令r(t)=0时，求得扰动输入作用下的误差传递函数为121211202120)1)(1()1()()(1)()(limlimKRsRKKssssKssGsGsNssGennssssn所以扰动稳态误差为由上式计算可以看出，r(t)和n(t)同是阶跃信号，由于在系统中的作用点不同，故它们产生的稳态误差也不相同。由扰动稳态误差的表达式可知1K提高系统前向通道中扰动信号作用点之前的环节的放大系数，可以减小系统的扰动稳态误差。该系统总的稳态误差为1KReeenssnssrss285)1()(111ssKsGsKsG2221)(为了分析系统中串联的积分环节对稳态误差的影响，假设图中系统总的稳态误差为0ssnssrsseee0)()(1)(210limsGsGssResssr)()()(1)(2120limsNsGsGssGesssn0)1)(1()1(21212120limsRKKssssKsns给定输入和扰动输入保持不变。这时，系统的稳态误差可按上述相同的方法求出，286比较以上两次计算的结果可以看出，•若要消除系统的给定稳态误差，在系统前向通道中串联的积分环节都起作用。•若要消除系统的扰动稳态误差，在系统前向通道中只有扰动输入作用点之前的积分环节才起作用。若要消除由给定输入和扰动输入同时作用于系统所产生的稳态误差，则串联的积分环节应集中在前向通道中扰动输入作用点之前。对于非单位反馈系统，当H（s）为常数时，以上有关结论同样适用。)(1sG11前面定义了相对于给定输入的无差度，同样也可以定义相对于扰动输入的无差度。当系统的中含有个串联的积分环节时称系统相对于扰动输入是阶无差系统，而称为系统相对于扰动输入的无差度。对本例中的前一种情况，系统对扰动输入的无差度为0，而后一种情况，系统对扰动的无差度是1。谈及系统的无差度时，应指明是对哪一种输入作用而言，否则，可能会得出错误的结论。13.5.43.5.4减小或消除稳态误差的方法减小或消除稳态误差的方法前面分析表明，为了减小系统的稳态误差，可以增加开环传递函数中的串联积分环节的数目或提高系统的开环放大系数。但是，串联的积分环节一般不超过2，而开环放大系数也不能任意增大，否则系统将可能不稳定，为了进一步减小系统稳态误差，可以采用加前馈控制的复合控制方法，即从给定输入或扰动输入处引出一个前馈控制量，加到系统中去，通过适当选择补偿装置和作用点，就可以达到减小或消除稳态误差的目的。288在图示系统中，为了消除由r(t)引起的稳态误差，可在原反馈控制的基础上，从给定输入处引出前馈量经补偿装置对系统进行开环控制。)(sGc按给定输入补偿的复合控制)()()(1)]()(1[)(212sRsGsGsGsGsEc整理得)(1)(2sGsGc如果选择补偿装置的传递函数为则系统的给定稳态误差为零。)]()()()()[()()(12sRsGsEsGsGsRsEc此时系统误差信号的拉氏变换式为)(sGc)(1sG)(2sGR(s)E(s)C(s)-+289在图示系统中，为了消除由n(t)引起的稳态误差，可在原反馈控制的基础上，从扰动输入引出前馈量经补偿装置加到系统中，)(sGc)(1sG)(2sG)(sGcR(s)N(s)E(s)--+C(s)A按扰动输入补偿的复合控制)]()()()()()()[()(112sCsGsNsGsGsNsGsCc若设r(t)=0，则系统的输出C(s)就是系统的误差信号。系统输出的拉氏变换式为)()()(1)]()(1)[()(2112sNsGsGsGsGsGsCc整理得)(1)(1sGsGC如果选择补偿装置的传递函数为可使输出不受扰动n(t)的影响，故系统的扰动稳态误差为零。290从结构上看，当满足时，扰动信号经两条通道到达A点，两个分支信号正好大小相等，符号相反，因而实现了对扰动的全补偿。)(1)(1sGsGC前馈控制加入前后，系统的特征方程保持不变，因此，系统的稳定性不会发生变化。291例3.13控制系统如图所示(1)计算扰动引起的稳态误差；(2)选择合适的K值，使系统在输入作用下无稳态误差。ttr)(ttn)(E(s)--KK1K3sK2)1(4TssK)(sC)(sR)(sN292413en0ssn)()(limKKKsNsses4213224c421)1()1()(KKKTssKKTsssKKKKKs（2）闭环传递函数等效单位反馈系统的开环传递函数sKKKKTKKTsssKKKKKsssG)()1()(1)()(4c323224c421432c4c32,0KKKKKKKK解（1）要使系统在作用下稳态误差为0，ttr)(系统应为2型系统)()()(sNsEsen))(1(1132421KKsTssKKK293作业P72.3-15p73.3-18294第四章频率特性法第四章频率特性法频率特性的概念典型环节频率特性绘制频率特性图奈氏稳定判据相对稳定性频域响应分析2951111)()()(11TssCRsUsUsGrc22sinωsAω(s)U,则tAu设rr22csA1Ts1sU)()sin(11)(22/22TarctgtTAeTtAtuTtc)sin(122TarctgtTA稳态分量TarctgTA)(,1/1)(22相频特性性定义网络系统的幅频特jsTjarctg22Ts11Tj11eT11频率特性：数学本质R1C1i1(t)4.14.1频率特性的概念频率特性的概念296扩展为一般系统)(sC)(sR)(sG))(()(sin)(22jsjsAsAsRtAtR其中)())(()()()()()()(21nsssssssNsDsNsRsCsGnnssassajsbjsbsRsGsC11)()()(则tsntstjtjneaeaebbetc11)(反拉氏变换得系统输出的稳态分量为tjtjwebbetc)(297j2AjGjsjsjsAsGbj2AjGjsjsjsAsGbjsjs)()())(()()()())(()(＝＝其中)()()(jejGjGG(jw)和G(－jw)为复数，可用复数的模和相角的形式表示为)()()()()(jjejGejGjG)(Re)(Im)()(jGjGarctgjG＝其中)sin()(2)(2)(2)()()()()()(tAjGjeeAjGjAeejGjAeejGtctjtjtjjtjjw298的函数它们都是通称为系统的频率特性称为相频特性称为幅频特性)(Re)(Im)()(jGjGarctgjGjG)()()()(jGjjsejGsGjG注意：反应了系统在不同频率的正弦输入信号作用下，稳态输出的幅值和输入信号幅值之比。反应了系统在不同频率的正弦输入信号作用下，输出信号相对于输入信号的相位位移。)(jG)(jG299物理意义300比较系统的频率特性和传递函数、微分方程可知，它们之间存在右述关系微分方程d/dt=s传递函数s＝jw频率特性d/dt=jw01110111)()()()()()()(ajajajabjbjbjbjGnnnnmmmm那么01110111)(asasasabsbsbsbsGnnnnmmmm设由实验方法获得根据稳态输出的幅值比和相位差得到不能针对不稳定系统，因为会存在振荡和发散系统的频率特性的获取由传递函数（或微分方程）可以得到系统的频率特性：301•基本思想–将控制系统的各个变量看成一些信号，而这些信号又是由不同频率的正弦信号合成的；各个变量的运动就是系统对各个不同频率的信号的响应的总和。•特点–物理意义鲜明，有很大的实际意义。–计算量小。它与过渡过程的性能指标有对应关系，不必解出特征根。–由于采用作图，使用这种做法有很强的直观性。–应用对象广泛。不仅适用于二阶系统，也适用于高阶系统；不仅适用于线性定常系统，也可推广应用于某些非线性系统。尤其系统在某些频率范围存在严重的噪声时，应用频率特性法可以比较满意地抑制噪声。3024.2.4.2.典型环节频率特性典型环节频率特性•幅相频率特性曲线简称幅相曲线，又称极坐标图。在复平面上，以角频率为自变量，把频率特性的幅频特性——模和相频特性——相角同时在复平面上表示出来的图就是幅相曲线。•开环对数频率特性图(对数坐标图或Bode图)包括开环对数幅频曲线和开环对数相频曲线横坐标为，以对数分度，十倍频程，单位是rad/s频率每扩大10倍，横轴上变化一个单位长度。因此，对于坐标分度不均匀，对于lg则是均匀的。4.2.1常用于描述频率特性的几种曲线常用于描述频率特性的几种曲线303•幅频特性是的偶函数•相频特性是的奇函数•性能分析（尤其是稳定性）时不需要绘制精确的幅相特性曲线，只需绘制大致形状即可:0:0的曲线和的曲线关于实轴对称304伯德（Bode）图又叫对数频率特性曲线，它是将幅频特性和相频特性分别绘制在两个不同的坐标平面上，前者叫对数幅频特性，后者叫对数相频特性。两个坐标平面横轴（ω轴）用对数分度，对数幅频特性的纵轴用线性分度，它表示幅值的分贝数，即；对数相频特性的纵轴也是线性分度，它表示相角的度数，即。通常将这两个图形上下放置（幅频特性在上，相频特性在下），且将纵轴对齐，便于求出同一频率的幅值和相角的大小，同时为求取系统相角裕度带来方便。)()(lg20)(dBjGL（度）)()(jG305301.02lg4771.03lg602.04lg699.05lg778.02lg3lg6lg845.07lg903.02lg38lg954.03lg29lg对数分度：)(w对数相频特性的纵坐标为对数相频特性的函数值，单位是度。表示为对数幅频特性的纵坐标为对数幅频特性的函数值，采用线性分度，单位是dB。表示为L(w)=20lgG(jw)306s/rad)(L0.1110100dB2040线性分度f2(弧度/秒)0.1110100)(s/rad¶È900£­900线性分度(弧度/秒)307对数频率特性优点–展宽频率范围–对于不含不稳定环节的系统，可由对数频率特性得到系统的传函。–典型环节可用直线或折线近似表示212121)(2)(121)(.)()()(jjjeGGejGejGjGjG2121lg20lg20lg20GGGG2121GG211GG211GG2121lg20lg20GG几个频率特性相乘，对数幅、相曲线相加两个频率特性互为倒数，幅、相特性反号，关于轴对称3084.2.2.4.2.2.典型环节的频率特性典型环节的频率特性•比例环节•积分环节•惯性环节•振荡环节•一阶微分环节•二阶微分环节•延时环节•不稳定环节309比例环节传递函数G(s)=k频率特性G(jw)=kk1）幅相曲线幅频特性G(jw)=k00)(jwG相频特性幅相曲线如右图所示310由图可看出比例环节的幅频特性为常数K，相频特性等于零度，它们都与频率无关。理想的比例环节能够无失真和无滞后地复现输入信号。31100)(2010lg20)(dBL0.1110100)(s/rad¶È00s/rad)(L0.1110100dB2000)(lg20)(kL2)对数频率特性曲线若k=10312比例环节的对数幅频特性如图所示，它是一条与角频率ω无关且平行于横轴的直线，其纵坐标为20lgk。当有n个比例环节串联时，即幅值的总分贝数为01011020Klog20dB)(L1010010001001000000100900180度）（10比例环节的Bode图nKKKjG21)(nKKKjGlg20lg20lg20)(lg2021比例环节的相频特性是如图所示，它是一条与角频率ω无关且与ω轴重合的直线。00)(jG313积分环节09011)(1)(ejjjGssG幅频特性G(jw)=1/090)(jG0)(0由时，由jG相频特性幅相曲线如右图所示1）幅相曲线314积分环节09011)(1)(ejjjGssG2）对数频率特性lg201lg20)(L这是一条在=1处穿过横轴的直线，其斜率为dB20lg2010lg201lg20101lg20即频率变化10倍，对数幅值下降－20dB3150.1110100)(s/rad¶È00-900s/rad)(L0.1110100dB20-20-20dB/dec090)(思考题：如果有n个积分环节，那么它们的频率特性如何？当有n个积分环节串联时，即其对数幅频特性为是一条斜率为-n×20，且在ω=1（弧度/秒）处过零分贝线（ω轴）的直线。相频特性是一条与ω无关，值为-n×900且与ω轴平行的直线。两个积分环节串联的Bode图如图所示。njjG)(1)(lg201lg20)(lg20njGn090)(njG两个积分环节串联的Bode图090001.010180090度）（01.0040decdB/40dB)(L01.01.011031711Ts)s(G222211111)(TTjTTjjGTarctgjwGTjwG)(,1)(1)(2惯性环节318当时，当时，当时，当ω由零至无穷大变化时，惯性环节的频率特性在平面上是正实轴下方的半个圆周，证明如下：令2211)(TjGTarctgjG)(01)0(jG00)0(jGT1707.021)1(TjG045)1(TjG0)(jG090)(jG)(jG222211111)(TTjTTjjG)(11)(Re22uTjG319则有这是一个标准圆方程，其圆心坐标是，半径为。且当ω由时，由，说明惯性环节的频率特性在平面上是实轴下方半个圆周，如图所示。惯性环节是一个低通滤波环节和相位滞后环节。在低频范围内，对输入信号的幅值衰减较小，滞后相移也小，在高频范围内，幅值衰减较大，滞后相角也大，最大滞后相角为90゜。)(1)(Im22vTTjG2222222222112111)(21)(TTTvu0,21210)(jG900)(jG3201）幅相曲线如图。惯性环节为相位滞后环节，最大的滞后相角为90度。当时，当时，用两条直线近似描述惯性环节的对数幅频特性。22221lg2011lg20)(lg20TTjGT1T1)(01lg20)(lg2022dBTjG)(lg201lg20)(lg2022dBTTjG（2）对数频率特性曲线惯性环节的频率特性是其对数幅频特性是11)(jTjG32200090)(lg20)(1145)(3)()1(10)(0)(11TLTTdBLTTdBLTT讨论：用渐近线表示：)(LTlg)(LTdB)(LT20101323很明显，距离转折频率愈远愈能满足近似条件，用渐近线表示对数幅频特性的精度就愈高；反之，距离转折频率愈近，渐近线的误差愈大。等于转折频率时，误差最大，最大误差为T1)11(TT或T/1)(32lg201lg20122dBTT渐近特性decdB/20精确特性图惯性环节的Bode图)()(Ldb1001020T1201T1101T151T1T12T110T12000045090324时的误差是时的误差是误差曲线对称于转折频率，如图所示。由图可知，惯性环节渐近线特性与精确特性的误差主要在交接频率上下十倍频程范围内。转折频率十倍频以上的误差极小，可忽略。经过修正后的精确对数幅频特性如图所示。T121)(97.025lg201lg202122dBTTT12)(97.02lg205lg20)lg20(1lg20121222dBTTTTT1T1325db01234T1101T151T121T1T12T15T110惯性环节对数幅频特性误差修正曲线326惯性环节的相频特性为当时，当时，当时，对应的相频特性曲线如下图所示。它是一条由00至-900范围内变化的反正切函数曲线，且以和的交点为斜对称。TarctgjG)(000)0(jGT1045)1(TjG090)(jGT1045)(jG327s/rad)(LdB20-20T1T10T.10-20dB/dec)(s/rad¶È00-900-450T1T.10T1007.5)(04.0)(1.0dBLT0384042010.)(dB.)(LT328振荡环节121/12)(22222TssTTnsssGnnnTj)T()j(G211222222222212)(4)1(1)(TTarctgjGTTjG1）幅相曲线0,1,090,21,1T180,0,ω=T1ζ减小1ReIm329当时，，当时，，当时，，振荡环节的幅频特性和相频特性均与阻尼比ξ有关，不同阻尼比的频率特性曲线如图所示。2212)(TTarctgjG1)(jG21)(jG000)(jGT1090)(jG0)(jG0180)(jG)1(rrMMr041)(222222TTddjGdd)210(2121122nrT当阻尼比较小时，会产生谐振，谐振峰值和谐振频率由幅频特性的极值方程解出，谐振时幅值大于12222224)1(1)(TTjG330其中称为振荡环节的无阻尼自然振荡频率，它是振荡环节频率特性曲线与虚轴的交点处的频率。将代入得到谐振峰值为将代入得到谐振相移φr为Tn1r)(jGrM)210(121)(2rrjGMr)(jG221)(arctgjGrrnnrM01/nTnr0mIr1eRG图振荡环节的频率响应其中称为振荡环节的无阻尼自然振荡频率，它是振荡环节频率特性曲线与虚轴的交点处的频率。将代入得到谐振峰值为将代入得到谐振相移φr为Tn1331振荡环节的幅值特性曲线如图所示。在的范围内，随着ω的增加，缓慢增大；当时，达到最大值；当时，输出幅值衰减很快。当阻尼比时，此时振荡环节可等效成两个不同时间常数的惯性环节的串联，即r0)(MrrM)(Mr11)(M0rrM图振荡环节的频率响应11111)(21sTsTsGT1，T2为一大一小两个不同的时间常数，小时间常数对应的负实极点离虚轴较远，对瞬态响应的影响较小。振荡环节为相位滞后环节，最大的滞后相角为180度。3322122222120)T()T(lg)(L平方项4次方项2212)(TTarctg0n90220L1T2)(,lg)(,Tn1转折频率0T2T120L0dB0120L1T122220n)()(lg)()(,lg)(,误差)lg()()(lg)()(,lg)()(lg)(,T40T2T120L180T40T2T120L1T3222202222n2）对数频率特性333当时，当时，渐近线的第一段折线与零分贝线（ω轴）重合，对应的频率范围是0至；第二段折线的起点在处，是一条斜率为-40（dB/dec）的直线，对应的频率范围是至∞。两段折线构成振荡环节对数幅频特性的渐近线，它们的转折频率为。对数幅频特性曲线的渐近线如图所示。T1)(04)1(lg20222222dBTTT1)(lg404)1(lg20222222dBTTTT1T1T1T10decdB/404020dB)(L高频渐近线T1101T1T110低频渐近线334渐近线与精确对数幅频特性曲线的误差分析如下：它是阻尼比ξ的函数；当ξ=1时为-6（dB），当ξ=0.5时为0(dB)，当ξ=0.25时为+6(dB)；误差曲线如图4-18所示。0decdB/404020dB)(L高频渐近线T1101T1T110低频渐近线图4-17振荡环节渐进线对数幅频特性1T2lg204)1(lg201222222TTT8.0图4-18振荡环节对数幅频特性误差修正曲线db1612840481.02.03.04.06.08.00.1234681005.01.015.02.025.03.04.05.06.00.1335由图知，振荡环节的误差可正可负，它们是阻尼比ξ的函数，且以的转折频率为对称，距离转折频率愈远误差愈小。通常大于（或小于）十倍转折频率时，误差可忽略不计。经过修正后的对数幅频特性曲线如图所示。由图可看出，振荡环节的对数幅频特性在转折频率附近产生谐振峰，这是该环节固有振荡性能在频率特性上的反映。前面已经分析过，谐振频率ωr和谐振峰Mr分别为T1db)(L20040T1101T1T11005.00.15.0decdb/40图振荡环节对数幅频率特性图T1336其中称为振荡环节的无阻尼（ξ=0）自然振荡频率，它也是渐近线的转折频率。由式可知，当阻尼比ξ愈小谐振频率ωr愈接近无阻尼自然振荡频率ωn，当ξ=0时，ωr=ωn振荡环节的相频特性是)210(212nr2121)(rrjGMTn12212)(TTarctgjG337当时，当时，当时，除上面三种特殊情况外，振荡环节相频特性还是阻尼比ξ的函数，随阻尼比ξ变化，相频特性在转折频率附近的变化速率也发生变化，阻尼比ξ越小，变化速率越大，反之愈小。但这种变化不影响整个相频特性的大致形状。不同阻尼比ξ的相频特性如图所示。000)0(jGT1090)1(TjG0180)(jGT1000900180n101Tn1n1005.00.1图振荡环节对数相频特性338)(s/rad¶È00-900T1T.10T10-1800s/rad)(LdB20-20T1T10T.10-40dB/dec-40相频特性也是关于的函数，关于－90度斜对称。,w精确值和近似值之间存在的误差和相关；并且越小，误差越大。)(L339一阶微分环节1)(1)(jwTjGsTsG幅频特性相频特性arctgwTjGTwjG)(1)(2211）幅相曲线00090jGjG45T1jG2T1jGT100jG10jG0)(,)()(,)()(,)(时，＝当时，＝当时，＝当211GG211GG2121lg20lg20GG两个频率特性互为倒数，幅、相特性反号，关于轴对称340频率特性如图所示。它是一条过点（1，j0）与实轴垂直相交且位于实轴上方的直线。纯微分环节的频率特性与正虚轴重合。1eR0mIG0G图一阶微分环节的频率响应341其对数幅频特性是当时，当时，一阶微分环节的对数幅频特性如图所示，渐近线的转折频率为，转折频率处渐近特性与精确特性的误差为，其误差均为正分贝数，误差范围与惯性环节类似。相频特性是当时，；1)(TjjG1lg20)(lg2022TjGT1)(01lg2022dBTT1)(lg201lg2022dBTTT/1arctgTjG)(000)0(jGdB32lg202）对数频率特性342当时，；当时，。一阶微分环节的相频特性如图所示，相角变化范是00至900，转折频率处的相角为450。比较可知，一阶微分环节与惯性环节的对数幅频特性和相频特性是以横轴（ω轴）为对称的。T1090)(jG045)1(TjGT120100db)(L1100111011110110011001101110111001)(度09004500一阶微分环节的Bode图decdB/20渐近特性精确特性343s/rad)(LdB20-20T1T10T.1020dB/dec900)(s/rad00450T1T.10T10度22Tw120Llg)(arctgwT)(344二阶微分环节222)(nnsssGTjTjG2)1()(222222222212)(4)1()(TTarctgjGTTjG1）幅相曲线000180)(,)(90)1(,2)1(10)0(,1)0(0jGjGTjGTjGTjGjG时，＝当时，＝当时，＝当345由上可见，二阶微分环节和振荡环节的对数频率特性互为镜像。s/rad)(LdB40-40T1T10T.1040dB/dec900)(s/rad001800T1T.10T10度2122222120)T()T(lg)(L22112TTtg)(2）对数频率特性346)(s/rad¶È00-900T1T.10T10-1800s/rad)(LdB20-20T1T10T.10-40dB/dec-40振荡环节的bode图347延时环节sesG)(sincos)(jejGj1G幅相曲线和对数频率特性曲线分别是（度）（弧度）3.57)(jG348)(01lg20)(lg20dBjG（度）（弧度）3.57)(jG其对数幅频特性和相频特性分别为jejG)(延时环节伯德图如图所示。其对数幅频特性与ω无关，是一条与ω轴重合的零分贝线。滞后相角分别与滞后时间常数τ和角频率ω成正比。dB)(L0)(度001111003.5701000200图延时环节的Bode图34911)(TssG11)(jTjG不稳定环节的传递函数为不稳定环节有一个正实极点，对应的频率特性是不稳定环节350幅频特性和相频特性分别为当时，，当时，，当时，，不稳定环节的频率特性如右图。比较图可知，它与惯性环节的频率特性相比，是以平面的虚轴为对称的。11)(22TjG0()1801TGjarctgarctgT01)0(jG0180)0(jGT121)1(TjG0135)1(TjG0)(jG090)(jG0ImRe0图不稳定惯性环节的频率特性351•不稳定单元11Ts11Ts以上模相等，都是且与惯性环节相同，相频特性则不同，分别如下所示1)(1)(2TjwG9001Tarctg90180)18090(1Tarctg352幅相曲线都是半圆,分别为思考题：画出它们的对数频率特性图。不稳定的振荡环节推导类似。不稳定环节的对数幅频特性图和稳定环节相同，相频特性变化范围不同。3534.34.3绘制频率特性图绘制频率特性图0•绘制幅相曲线由典型环节的幅相曲线得到一般系统的幅相曲线一般用于分析稳定性由从，首先计算起点和终点的情况，其次分析变化的趋势，绘出相应的幅相曲线。354解：开环频率特性为例4-1.绘制如下开环传递函数的幅相曲线)0,,()1)(1()(2121均大于开KTTsTsTKsG1111)(21TjTjKjG开幅频特性和相频特性分别为11)(222212TTKjG开21)(TarctgTarctgjG开00180)(,0)(0)0(,)0(0jGjGjGKjG开开开开时，＝当时，＝当355曲线与虚轴相交时，相角为90度02190TarctgTarctg021221901TTTTarctg211TT2121)(TTTTKjG开＝0＝2121TTTTK356212121)(2)(121)(.)()()(jjjeGGejGejGjGjG2121lg20lg20lg20GGGG2121GG几个频率特性相乘，对数幅、相曲线相加若系统增加一个积分环节（1型系统）则11)(222212TTKjG开21090)(TarctgTarctgjG开)1)(1()(21sTsTsKsG开00270)(,0)(90)0(,)0(0jGjGjGjG开开开开时，＝当时，＝当357幅相曲线如图所示＝0＝2121TTTKT)(21TTK为求曲线范围和其与实轴的交点将频率特性写成实部和虚部的形式:)1)(1()]1()([)(22221222121TTTTjTTKjG开因此在起点，=0，可得到)](Im[)()](Re[21jGTTKjG开开求曲线和实轴的交点（对系统的稳定性很重要）212121)](Re[10)](Im[TTTKTjGTTjGx开开令358若系统再增加一个积分环节（2型系统）1111)(1)(212TjTjjKjG开那么00360)(,0)(180)0(,)0(0jGjGjGjG开开开开时，＝当时，＝当＝0＝幅相曲线如图所示359若系统含有积分环节，曲线起点为无穷远处，相角为v×(-900)，其中v积分环节个数。2）终点开环传函分母的阶数n大于分子的阶数m时，即n>m时，终点在原点，进入角度为(n-m)×(-900)n=m时，终点在正实轴上某点，坐标和各参数有关。综上所述，对于开环传递函数只含有左半平面的零极点的系统，其幅相曲线的起点和终点满足以下规律：1）起点若系统不含有积分环节，起点为（K,0）。360作业P1084-2(1,4),P1104-10(4)361•绘制对数频率特性图–叠加法：将各典型环节的图叠加。nnjnjnjeGGejGejGjG111)()(1)()()(nGGGGGlg20lg20lg20lg20121nG1因此一般系统的对数频率特性图可由典型环节叠加。)()()()(21sGsGsGsGn设由前述，可得362比例环节积分环节惯性环节震荡环节s/rad)(L0.1110100dB20s/rad)(L0.1110100dB20-20-20dB/decs/rad)(LdB20-20T1T10T.10-20dB/decT110decdB/40dB)(LT1101T1典型环节的对数幅频特性图363一阶微分环节二阶微分环节延时环节s/rad)(LdB20-20T1T10T.1020dB/decs/rad)(LdB40-40T1T10T.1040dB/dec典型环节的对数幅频特性图s/rad)(L0.1110100dB364–分段法：第一步：确定转折频率（惯性、振荡、比例微分环节)，标注在ω轴上；第二步：确定低频段Bode图位置，包括高度和斜率。vj20K20L0lglg)(位置＝在第三步：依次画转折频率以后部分，增减斜率。在交接频率处，曲线斜率发生改变,改变多少取决于典型环节种类.在惯性环节后,斜率减少20dB/dec;而在振荡环节后,斜率减少40dB/dec斜率由积分环节决定v＝00dB/decv=1-20dB/decv=2-40dB/dec第四步：在转折频率附近进行修正，得到较为精确的曲线。最左端直线斜率为:-20ν·dB/dec,这里ν是积分环节数。365090)(lg20)(－LdecdB203311T1//斜率＝＝＝转折频率00dB5175720k20L)(,..lglg)(例4-2：绘制对数频率特性图)121)(121()131(5.7)(2ssssssG开解：采用分段法。系统包括以下5个环节(1)比例(2)积分(3)比例微分decdB/20斜率Tarctg)(366(5)振荡decdBT/4022/111斜率＝＝＝转折频率(4)惯性decdBT/2022/111斜率＝＝＝转折频率arctgwT)(2212)(TTarctgω1＝1.414－40ω2＝2－20ω3＝3＋20总结转折频率和相应斜率，得到k201Lkk1Nlg)(,位置＝在367)(L0.1110dB2040600.01(1)(2)(3)(5)-20+20-20-40-60-60-80-20-40-601.41423368)(¶È900£­900s/rad0.11100.01-1800-2700(1)(2)(3)(4)(5)对数相频特性：1）将积分、惯性、比例微分、振荡环节分别画出相频特性曲线2）确定几个点（查表等），光滑连接369什么是剪切频率？开环幅频特性曲线（折线）过0分贝的频率。也叫剪切频率或穿越频率。记为c。s/rad)(L0.1110dB2040600.01-20-60-60-80-20-40-6017.51.41423c370剪切频率求法1)作图法——作精确的幅频特性图来求得2）计算法通过比例关系求得28041412601414120k20clg.lg.lglg因此342c.5.175.7lg20lg20k11.41423-20-60-80wc20lgkdBa0.31414.1lg20414.11)下降了从dBb0.9414.12lg602414.1)下降了从dBc1.1423lg8032)下降了从可以断定wc在2和3之间371例4-3绘制幅相曲线和对数频率特性图)101.0)(11.0)(110()15.0(100)(ssssssG1)讨论幅相曲线大致形状：-1ImRe∞ωω0ω1)-180)(1232)(0)(,0小于（时，当点位置如图所示，从从则从当jwGjGjGjG解：系统的频率特性为)101.0)(11.0)(110()15.0(100)(jjjjjjG37250tg010tg10tg10tg90.arg.arg.argarg)(2）对数频率特性图相频特性：见下页图计算剪切频率2lg201.02lg401.01lg20100lg20c5c0.11210-40-20wc373-900-1800-270000-20-20-40-40-600.11210100c374–一般说来，如果系统稳定且极点数多于零点数那么,如果幅频特性的斜率为如果幅频特性的斜率为–当系统不含有不稳定环节时（即系统只有左半平面的零极点），系统的相频特性随幅频特性的增加（或减少）而增加（或减少).所以只需要画它的对数幅频特性图即可。–精确的频率特性图是在近似图基础上，在转折频率附近描点，然后连成光滑的曲线即可220对应的相角为2)20(vv对应的相角为375最小相角系统和非最小相角系统的区别最小相角(相位)系统的零点、极点均在s平面的左半闭平面，在s平面的右半平面有零点或极点的系统是非最小相角系统。11)(,11)(:TssGTssG例如有两个传递函数20-20ωL(dB)10L(dB)50-20-40100ω)1.01(10)(ssG)01.01()(ssKsG50K幅频特性相同，但对数相频曲线却不相同。最小相角系统的幅频特性和相频特性一一对应，只要根据其对数幅频曲线就能写出系统的传递函数。如：376最小相角系统和非最小相角系统的区别最小相角(相位)系统的零点、极点均在s平面的左半闭平面，在s平面的右半平面有零点或极点的系统是非最小相角系统。L(dB)ω-40-40-20ω1ωcω2)1()1()(221sssKsGccKK1121,377作业P1114-10（3），4-17（a,c)可以不画出相频特性曲线。3784.4奈氏稳定判据奈奎斯特(Nyquist，简称奈氏)稳定判据–根据开环频率特性对闭环系统的稳定性进行判断。–作图分析，计算量小，信息量大。–不但判稳定，也能给出不稳定根的个数和稳定裕量。1932年，美国Bell实验室的奈奎斯特提出了这样一种方法。这种方法是以系统的开环幅相频率特性曲线判别系统的稳定性，称为奈奎斯特稳定判据。3794.4.14.4.1数学基础数学基础–复变函数映射概念例：32sssF)(jSƽÃæImReFƽÃ棭2£­3ÎÞÇîÔ¶µãÔ­µã若在S平面上，任取一封闭轨迹，且使其不通过F(s)的奇点，则在F平面上就有一封闭轨迹与之对应。Fs380•柯西幅角原理对于复变函数)ps()ps)(ps()zs()zs)(zs(k)s(Fnm2121在s平面上封闭曲线C域内共有P=n个极点和Z=m个零点，且封闭曲线C不穿过F(s)的任一个极点和零点。当s顺时针沿封闭曲线C变化一周时，函数F(s)在F平面上的轨迹将按逆时针包围原点N=P–Z次。(零点个数考虑重根数，N>0逆时针，N<0顺时针。)381ImReFƽÃæjSƽÃæs即幅角原理的表达式为：N=P-Z其中N为曲线按逆时针绕原点的圈数，P为内包含的F(s)的极点数，Z为内包含的F(s)的零点数。FsN=1-3=-2382jSƽÃæImReFƽÃæjSƽÃæImReFƽÃæN＝0-1=-1N=1-0=13834.4.24.4.2奈氏稳定判据奈氏稳定判据•利用柯西复角原理判断稳定的思路：–使封闭曲线与频率特性相联系–使F(s)与系统闭环传递函数相联系–封闭曲线域为右半平面（或左半平面）384D形围线和Nyquist图：沿虚轴顺时针包围右半平面的闭曲线称为D形围线。jSƽÃæImReFƽÃæDÐÎΧÏßNyquistͼjj1半径无限大385开环传递函数)()()()()(000sDsNsHsGsG)()()(1)()()(1)()(0sDsNsGsGsHsGsGsGccC)()()()()()()(1)(1)(0000000sDsDsDsNsDsDsNsGsFCDC(s)闭环特征多项式；D0(s)开环特征多项式闭环传递函数闭环传递函数分母(辅助函数)G(s)H(s)+-386)()()()()()()(1)(1)(0000000sDsDsDsNsDsDsNsGsFCDC(s)闭环特征多项式D0(s)开环特征多项式闭环传递函数分母(辅助函数)F(s)三个特点：1.零、极点分别为闭、开环特征根;2.零、极点个数相等（分子分母阶数相同）;对于稳定的最小相角系统，从0时F(s)应不包围原点。3.与G(s)H(s)相差为1。如果辅助函数F(s)的零点都具有负的实部，即都位于S平面左半部，系统就是稳定的，否则系统便不稳定。387•已知F(s)=1+G0(s)，s平面上的D形围线在F平面上映射的有向闭曲线称为在F平面的奈奎斯特图。F(s)平面上的原点即G0(s)平面上的(－1，j0)点jSƽÃæImReFƽÃæDÐÎΧÏßNyquistͼjj1G0ƽÃæIm'(-1,j0)F(s)=1+G0(s)388根据柯西复角原理，对于复变函数F(s)=1+G0(s)，当s平面上顺时针沿D形围线连续变化一周时，则在F平面上和G0(s)平面上的奈奎斯特图逆时针包围原点和(-1,j0)点N次。N=P―ZD0(s)=0的根，G0(s)在右半平面的极点，开环极点DC(s)=0的根，系统特征方程的极点，闭环极点注意：顺时针转N<0;逆时针转N>0。P:在右半平面开环特征根数;Z:在右半平面闭环特征根数;N:在[G0]平面，从-，幅相曲线绕（-1，j0)点逆时针转过的圈数。389应用奈氏稳定判据判别系统稳定性，需要绘制或者由实验得到奈氏曲线，并确定奈氏曲线绕G0平面的（-1，j0）点的圈数N，在右半S平面的开环极点数P以及在右半S平面的闭环极点数Z=P-N。1）确定P：开环传递函数在右半S平面的极点数P是容易看出的。对于最小相位系统，P=0。3902）确定N的方法:为了确定N,将奈氏曲线从平面的下半部穿过负实轴的段,到平面的上半部1次,定义为1次负穿越;反之,奈氏曲线从的上半部穿过负实轴的段,到平面的下半部1次,定义为1次正穿越,如图4.7所示。0G),1(0G0G),1(0G[G0]0图4.7正，负穿越-1负穿越正穿越391若奈氏曲线正穿越次，负穿越次，则奈氏曲线绕平面的（-1，j0）点的圈数为：3）奈氏曲线的画法：因为奈氏曲线的精确形状，对于N值的确定并不重要，所以，只要根据一些特征画出奈氏曲线的大致形状即可。事实上，要在的范围内精确画出奈氏曲线也是不可能的，因为通常有无穷大，显然不可能画无穷大的坐标图。NN0GNNN392•开环频率特性G0(jω)和奈奎斯特图开环传递函数G0(s)，令s=jω，即开环频率特性G0(jω)当ω由0∞(负频部分无物理意义))()(00jGjG幅频特性相频特性D形围线（分为3段）在G0(s)平面上的映射就是系统在G0(s)平面上的奈奎斯特图，也就是ω从-∞到+∞时系统的开环幅相频率特性曲线。jsS平面D形围线-jj半径无限大123393•注意域的映射关系N=-2N=0jSƽÃæjjRe-1G0ƽÃæImRe-1G0ƽÃæIm394Nyquist稳定判据(在G0(s)平面上):必须使得Z=0(Z为不稳定闭环特征根的个数)。1.若系统开环稳定，则闭环系统稳定的条件是Nyquist图不包围(-1,j0)点。（N=P－Z=0－0＝0)2.闭环系统稳定的充要条件是N=P(N=P－Z=P所以Z=0)3.如果Nyquist图经过(-1,j0)，则系统临界稳定。4.如果Nyquist图的的变化范围为0到＋∞，那么Z＝P－2N推论：若Nyquist图顺时针包围(-1,j0)点，则系统一定不稳定。(N=P－Z,若N<0，P不会为负值，则必有Z≥1)395)j(G)j(G)j(G00000001800000)j(Gk)j(GImRe0j00k01800Nyquist图画法(示意图)(1)特殊点)jT)(jT(k)j(G11210例4-6已知开环传递函数判断系统稳定性396Nyquist判据(已知N,P求Z)P=0(由G0(s)表达式)N＝0(由Nyquist图)因为N＝P－Z,所以Z=0，故系统稳定。0018000)j(Gk)j(G单调递减单调递减0由正频部分（Nyquist图)Imk0j-1j0-负频部分(与正频对称)(2)趋势：39700027000100001)j(G)j(G02单调变化与实轴有交点，为－7.9(分母有理化，按虚实部讨论)100k,).)(.)(()(1j201j501jkjG0例4-7画Nyquist图：398Nyquist判据：N＝-2，P=0,N=P－Z，故Z=2。因此，k=100时，有两个极点在右半平面，系统不稳定。-7.9(-1,j0)ReIm100本系统是否稳定主要取决于奈氏曲线和实轴的交点是否小于－1。kk不稳定可能稳定所以经计算可得，交点与k相关，k越大，交点的坐标离虚轴越远。399积分环节个数v=1000018009001)s(G)s(G00018090)s(G0020)s(G从从从单调变化问题：N＝?)s(sk)s(G10例4-8ImRe-1积分环节下的奈氏稳定判据400j0000CBA放大s由于不能通过F(s)的奇点，所以改造D形围线，增加第4部分，即以原点为圆心，无穷小为半径的半园绕过虚轴上的极点（0，0）。这样就把s=0的极点归到左半平面4401在原点附近令jeS＝当从时202－jjjekek)e(G0)e(Gj02020)e(Gj2200022020)2(jjjekeksekABCA’B’C’402-1ImReA'B'C'00N＝0，P=0所以Z=0系统稳定则上述的无穷小圆弧4映射为从0－到0＋顺时针旋转的无穷大圆弧，绕行的角度为π。依次类推，当v>1时，4部分将映射为绕行角度为的无穷大圆弧403s的第（4）部分无穷小半圆弧在GH平面上的映射为顺时针旋转的无穷大圆弧，旋转的弧度为弧度。图4-9（a）、（b）分别表示当v=1和v=2时系统的奈氏曲线，其中虚线部分是s的无穷小半圆弧在GH平面上的映射。虚轴上有开环极点时的奈氏轨迹mI000R01veR)(aGH时的奈氏曲线0vj000)1()2(R)3()4(0rSs0010R0GH2veR)(bmI404小结：积分环节数v=1在无穷远处顺时针绕行v=2在无穷远处顺时针绕行v=n在无穷远处顺时针绕行n2Nyquist判据：已知开环极点数P积分环节数rNyquist图绕(-1,j0)点N求闭环极点数Z意味必须已知系统开环传递函数405应用奈氏判据分析系统稳定性时，可能会遇到下列三种情况：(i)当系统开环传递函数的全部极点都位于S平面左半部时（P=0），如果系统的奈氏曲线不包围GH平面的点（N=0），则闭环系统是稳定的（Z=P-N=0），否则是不稳定的；（ii)当系统开环传递函数有p个位于S平面右半部的极点时，如果系统的奈氏曲线逆时针包围点的周数等于位于S平面右半部的开环极点数（N=P），则闭环系统是稳定的（Z=P-N=0），否则是不稳定的；(iii)如果系统的奈氏曲线顺时针包围点（N<0），则闭环系统不稳定（Z=P-N>0）。（iv）当曲线恰好通过GH平面的点（注意不是包围），此时如果系统无位于S平面右半部的开环极点，则系统处于临界稳定状态。综上，奈氏曲线是否包围GH平面的点是判别系统是否稳定的重要依据。),1(j),1(j)()(sHsG)()(sHsGGHGHGHGHGH),1(j),1(j),1(j406作业P1114-4,4-7((b),(d)),4074.5.4.5.相对稳定性相对稳定性•相对稳定性——稳定裕度•求稳定裕度:解析法,奈氏曲线•增加稳定裕度的方法4.5.1相对稳定性——稳定裕度Routh判据和Nyquist判据给出系统绝对稳定的信息，但稳定程度如何，离不稳定边缘还有多远？这是工程上最关心的。由此引出稳定裕度相对稳定性——稳定裕度幅值裕度相角裕度408ImRe-1cg)j(Gg0••ImRecg-1)j(Gg0••幅值穿越频率0gg180j)(:对于奈氏曲线，在GH平面上，可以用奈氏曲线与(-1,j0)的靠近程度来表征系统的相对稳定性。离(-1,j0)越近，稳定程度越低。1jGc0c)(:相位穿越频率409其中，ωg为相位穿越频率。其定义的含义：如果系统的开环传递系数增大到原来的Kg倍，则系统处于临界稳定状态。)()(lg'or)()(.ggggggjHjG20KjHjG1K1)()(.cc00jHjG18020ωωgωcj-1G(jωc)H(jωc)G(jωg)H(jωg)0Kg(dB)(o)(dB)-180ωgωcω其中，ωc为幅值穿越频率。其定义的含义：如果系统对频率为截止频率的信号的相角滞后再增大度，则系统处于临界稳定状态。系统稳定，则Kg>1、>0。410相角裕量幅值裕量系统临界稳定系统不稳定系统稳定000jG180180c00c0)()(为负值系统临界稳定系统不稳定系统稳定1K1K1KjHjG1Kggggg0g)()(对于最小相位系统（开环传函不含右半s平面零极点的系统）：要综合两者考虑稳定性和相对稳定性，不能只考虑一个指标。411求稳定裕度1)解析法由前述相角裕度和幅值裕度的定义式来求。例4-10)252(40)()(2ssssHsG解：系统的开环频率特性为)225(40)()(2jjjHjG所以2022225290)()(4)25(401)()(arctgjHjGjHjG412由前述定义1)()(ccjHjG82.1c02005.8082.12582.1290)()(180arctgjHjGcc0180)()(ggjHjG5gdBjHjGKggg94.125.1lg20)()(1lg204132）幅相曲线法（极坐标图法）画极坐标图，画单位圆。按照右图得到相角裕度和，然后根据得到幅值裕度。)(0gjG))(/1lg(200ggjGKImRecg-1)j(Gg0•例4-10(续）用幅相曲线法作图如右所示，得到08094.1)8.0/1lg(208.0)(0ggKjG注意：要精确画图414例4-11)1()1()()(TsssKsHsG幅相曲线如右。由奈氏判据判断稳定性P=1N=1所以Z=P-N=0系统稳定由图知00))(/1lg(20ggjGK所以对于开环传递函数含有不稳定环节的系统，不能由稳定裕度来判断系统的稳定性。系统不稳定ImRecg-1•G(jwg)0－0++∞－∞4154.54.5频域响应分析频域响应分析在频域中对系统进行分析时，除了稳定性分析外，还要对系统的动态性能进行分析。频域性能指标有：幅值穿越频率，相位穿越频率，相角裕度，幅值裕度，谐振频率，谐振峰值，系统带宽和带宽频率等。超调量C(t)C(t)上升时间上升时间trtr峰值时间峰值时间tptp调节时间调节时间tsts误差带误差带稳态误差稳态误差)(too1.01.0tt控制系统性能指标控制系统性能指标416闭环频率性能指标零频值A(0)，Amax谐振频率wr和谐振峰值Mr带宽频率wb，A(wb)＝0.707A(0)wbwrA(0)Amax0.707A(0)w)21(1212rM)1(21112rrMM频域指标和时域指标的关系谐振峰值和系统超调量的关系，对于二阶系统2nn22nn2n0s2ssG2sssG)()()(417谐振频率及系统带宽与时域指标的关系%10021ep由%1001122rrrrMMMMpe得到可知Mr在1.2~1.5时，p＝20%~30%，系统将获得满意的过渡过程。)210(212nr22105.0ln11nsnptt2222105.0ln211121srprtt对于给定的阻尼比，二阶系统的谐振频率wr和tp、ts成反比。418同理，二阶系统带宽频率可由下式求出422222442)21(21)(2)(nbnnnbjj24222422105.01ln442)21(11442)21(sbpbtt同样，对于给定的阻尼比，二阶系统的带宽频率wb和tp、ts成反比。一般来说，频带宽的系统有利于提高响应速度，但同时又容易引入高频噪声，应均衡考虑419高低频段特性与动态性能的关系低频段主要影响静态特性，如稳态误差高频段要衰减得快些，抑制噪声相角裕度和阻尼比的关系)(2)()(22jjjGnno由开环频率特性和剪切频率定义1)(cojG得到242214)(nc240021422290180arctgarctgarctgcnnc－在时，它们之间近似为7.001.06.0~3.060~3000，当420作业P1114-14421小结：（1）频率特性是线性系统（或部件）在正弦函数输入下，稳态输出与输入之比对频率的关系，概括起来即为同频、变幅、相移。（2）熟记典型环节频率特性的规律及其特征点。（4）熟练掌握由系统开环传递函数绘制开环极坐标图和伯德图的方法。（6）正确理解奈奎斯特判据的原理证明和判别条件。（7）熟练掌握运用奈奎斯特判据判别系统稳定性的方法，并能正确计算稳定裕度。（8）正确理解谐振峰值、频带宽度、截止频率、相角裕度、幅值裕度等概念，明确其和系统阶跃响应的关系。422第五章线性系统的校正第五章线性系统的校正5.1基本概念5.2基本PID控制算法5.3PID参数对控制性能的影响5.4PID参数确定423设计一个自动控制系统一般经过以下三步:根据任务要求，选定控制对象；根据性能指标的要求，确定系统的控制规律，并设计出满足这个控制规律的控制器，初步选定构成控制器的元器件；将选定的控制对象和控制器组成控制系统，如果构成的系统不能满足或不能全部满足设计要求的性能指标，还必须增加合适的元件，按一定的方式连接到原系统中，使重新组合起来的系统全面满足设计要求。原系统控制器控制对象校正系统原系统校正装置能使系统的控制性能满足控制要求而有目的地增添的元件称为控制系统的校正元件或称校正装置.图5－1系统综合与校正示意图5.15.1基本概念基本概念424•必须指出，并非所有经过设计的系统都要经过综合与校正这一步骤，对于控制精度和稳定性能都要求较高的系统，往往需要引入校正装置才能使原系统的性能得到充分的改善和补偿。反之，若原系统本身结构就简单而且控制规律与性能指标要求又不高，通过调整其控制器的放大系数就能使系统满足实际要求的性能指标。控制系统包括两部分不可变部分：执行元件和测量元件一旦选定，其参数和结构就固定了。可变部分：当系统通过调节放大元件的参数仍不能满足系统性能指标时，我们要加入附加装置来改善系统性能。我们称之为校正装置。校正的实质就是通过系统的零极点来改变系统性能。425系统性能指标时域指标,pst超调量调节时间,pva静态误差系数KK,K常常将时域指标转化为相应的频域指标进行校正装置的设计闭环频域指标,rMr谐振峰值谐振频率b带宽频率开环频域指标c剪切频率,gK幅值裕度相角裕度426系统分析与校正的差别:•系统分析的任务是根据已知的系统，求出系统的性能指标和分析这些性能指标与系统参数之间的关系，分析的结果具有唯一性。•系统的综合与校正的任务是根据控制系统应具备的性能指标以及原系统在性能指标上的缺陷来确定校正装置(元件)的结构、参数和连接方式。从逻辑上讲，系统的综合与校正是系统分析的逆问题。同时，满足系统性能指标的校正装置的结构、参数和连接方式不是唯一的，需对系统各方面性能、成本、体积、重量以及可行性综合考虑，选出最佳方案.427校正装置的连接方式:(1)串联校正(2)反馈校正(3)前馈校正Gc(s):校正装置传递函数G(s):原系统前向通道的传递函数H(s):原系统反馈通道的传递函数428串联校正串联校正的接入位置应视校正装置本身的物理特性和原系统的结构而定。一般情况下，对于体积小、重量轻、容量小的校正装置(电器装置居多)，常加在系统信号容量不大的地方，即比较靠近输入信号的前向通道中。相反，对于体积、重量、容量较大的校正装置(如无源网络、机械、液压、气动装置等)，常串接在容量较大的部位，即比较靠近输出信号的前向通道中。Gc(s)G(s)H(s)R(s)Y(s)-6－2串联校正429反馈校正反馈校正是将校正装置Gc(s)反向并接在原系统前向通道的一个或几个环节上，构成局部反馈回路。G1(s)G2(s)Gc(s)H(s)R(s)Y(s)由于反馈校正装置的输入端信号取自于原系统的输出端或原系统前向通道中某个环节的输出端，信号功率一般都比较大，因此,在校正装置中不需要设置放大电路，有利于校正装置的简化。但由于输入信号功率比较大，校正装置的容量和体积相应要大一些。图6－4反馈校正430前馈校正：根据参考输入或扰动输入的大小进行，适合开环或闭环，为复合控制++--1()GS2()GS()nGSN(s)++--1()GS2()GSR(s)()rGSR(s)Y(s)Y(s)431•串联校正方式：PID比例、积分、微分•PID控制在工业上比较常用。其工作原理可由比例(P)、积分(I)、微分(D)三环节并联直观地说明。sTsTKsEsUsGdicc11)()()(频域形式：tdicdttdeTdeTteKtu0)()(1)()(时域形式：)(sU)(sEsTKiccKsTKdc432•为什么在工业过程控制中大都（将近90%以上）采用PID控制器？PID控制器作为工业控制中的主导控制器结构，其获得成功应用的关键在于，大多数过程可由低阶动态环节（一阶或二阶惯性加纯滞后）近似逼近，而针对此类过程,PID控制器代表了在不知道被控对象数学模型的基础上一个实用而廉价的解。PID不需要依赖于系统的传函。4335.25.2基本基本PIDPID控制算法控制算法•比例(P)控制•积分(I)控制•比例积分(PI)控制•微分(D)控制•比例微分(PD)控制•比例积分微分(PID)控制•基本PID控制算法小结4345.2.1比例(P)控制•比例（P）作用：+-)(sR)(sGc)(sY)(sU)(sEsT1eKcsc假设在初始稳态（平衡）条件下，有0)0(,0)0()0()0(uyre)(),(),(tutytr当时，在外界扰动影响下，实际各变量为：0t)()(teKtupKp为比例增益435)()(),())()((),()()(uKytutytrKtytrtecp)(11)(rKKepc以上结果也可直接从静态比例控制系统结构方框图获得。由上式可以看到，控制器的比例增益越大，控制稳态误差越小。但降低系统的相对稳定性，甚至可能造成闭环系统不稳定。考虑设定值阶跃扰动，在下，有式：0)()(rtr在稳态条件下，即当时，设定值阶跃输入导致的稳态偏差为：t436•优缺点–比例控制及时、快速、控制作用强，可提高系统的控制精度（即可降低系统的稳态误差）。–但其具有致命的缺点——有稳态偏差且降低相对稳定性甚至使系统不稳定。当扰动发生后，经过比例控制，系统虽然能达到新的稳定，但是永远回不到原来的给定值上。也就是说，新的平衡值相对于原来地平衡值有一差值。由第四章可知，比例控制使得稳定裕度减小，甚至小于0。4375.2.2积分(I)控制•积分作用：tideTtu0)(1)(优缺点前向通道上提高控制系统的型别，改善系统的稳态精度。积分作用在控制中会造成过调现象，乃至引起被控参数的振荡。因为u(t)的大小及方向，只决定于偏差e(t)的大小及方向，而不考虑其变化速度的大小及方向。积分作用滞后90度，对稳定性不利；且调节缓慢，不及时。()1()iUsEsTs传递函数为iT定义：为“积分时间常数”。4385.2.3比例积分(PI)控制在前向通道上，相当于系统增加了一个位于原点的极点，和一个s左半平面的零点，该零点可以抵消极点所产生的相位滞后，以缓和积分环节带来的对稳定性不利的影响。比例积分作用是比例作用和积分作用的综合01()()(),tpiutKetedT1()1()piUsKEsTs+-(t)r)11(sTKip)(ty)(tue(t)sTeKCsC1439•积分控制器的阶跃响应特性：iTeKc比例作用t)(tut比例积分作用)(te在单位阶跃偏差输入条件下，每过一个积分时间常数时间，积分项产生一个比例作用的效果。以此来测量的大小。iTiT比例积分作用主要用来改善系统的稳态性能4405.2.4微分(D)控制•微分作用：–微分作用是根据偏差变化的速度大小来修正控制。可称为“超前”控制作用，能有效地改善容积滞后比较大的被控对象的控制质量。–微分作用总是阻止被控参数的任何变化。–适当地加入微分控制，可有效抑制振荡、提高系统的动态性能。–实际中的微分控制由比例作用和近似微分作用组成。dtedTud4415.2.5比例微分(PD)控制比例微分作用是比例作用和微分作用的综合+-(t)r)1(sTKdp)(ty)(tue(t)sTeKCsC1()()()pddetutKetTdt()1()pdUsKTsEs442•微分控制器的阶跃响应特性dTdtdeTd比例作用t)(tut比例微分作用)(te斜坡输入在斜坡输入条件下，要达到同样的u(t)，PD作用要比单纯P作用快，提前的时间就是Td。443例：如下图所示，当Td为0和不为0时系统的阶跃响应有何区别？+-(t)r)1(sTKdp)(ty)(tue(t)sTeKPsP121Js解：当Td为0时系统闭环传函为2()()ppKCsRsJsK这是二阶无阻尼临界稳定系统。C(t)0t10,pnKJ其中系统响应曲线如上所示。444由特征方程可知，当，系统的。,,0pdJKT00C(t)1t当Td不等于0时系统闭环传函为2(1)()()pdpdpKTsCsRsJsKTsK系统响应曲线如下所示。可见微分控制增加的系统的阻尼，有助于改善系统的动态性能。4455.2.6比例积分微分(PID)控制•PID控制包含上述三种控制规律的调节器称为PID调节器它可以结合三种作用的优点（积分改善稳态性能，微分改善动态性能），较好的满足生产过程自动控制的要求。根据实际情况选择其三个参数：Kp、Ti、Td01()()()()tpdidetutKetedTTdt()11()pdiUsKTsEsTs446基本PID控制算法小结cKsEsU)()(P：sTsTKsEsUdic11)()(PID：sTKsEsUic11)()(PI：01()()()tciutKetedT01()()()()tcdidetutKetedTTdt()()cutKet4475.35.3PIDPID参数对控制性能的影响参数对控制性能的影响•Kp对过渡过程的影响增益Kp的增大，使系统的调节作用增强，但稳定性下降；•Ti对系统性能的影响积分作用的增强（即Ti下降），使系统稳态误差减小，但稳定性下降；•Td对系统性能的影响微分作用的增强（即Td增大），从理论上讲使系统的超前作用增强，稳定性得到加强，但高频噪声起放大作用。因而，微分作用不适合于测量噪声较大的对象。4485.4PID5.4PID参数确定参数确定PID参数确定的法则由齐格勒和尼柯尔斯提出，是在实验阶跃响应的基础上根据临界稳定系统的Kp值建立起来。不知道控制对象的数学模型时，这些法则依然有效。因此PID控制在实际中广泛应用。两种方法动态响应法临界增益法4495.4.1动态响应法步骤第一步：求取动态响应曲线。TK()1sKeGsTs上述的S形曲线的传函为将其拐点切线和时间轴和c(t)=K的交点可得到和T的值，如上图所示第二步：估计被控对象的传递函数。450第三步：由齐格勒－尼柯尔斯给出的调整法则表，确定PID参数。控制器类型KpTiTdPPIPID/T0.9/T1.2/T3.32000.5因此可得21()1111.2(10.5)0.62PIDpdisTGKTssTTsssPID控制器有一个位于原点的极点和两个左半平面的零点451注意系统开环下测出阶跃响应单位阶跃响应曲线为S形。能保证阶跃响应的最大峰值和第二峰值之比为4:1可进行系统微调。被控对象有积分环节和复数极点时不适用。4525.4.2临界增益法临界增益法在系统闭环情况下进行-()cGs对象,0idTT步骤第一步：令，将控制器设置为比例控制。将Kp从0增大，首次出现等幅振荡时，记下此时的增益为Kps和振荡周期Ts。第二步：由齐格勒－尼柯尔斯给出的调整法则表，确定PID参数。453控制器类型KpTiTdPPIPID000.5Kps0.45Kps0.6Kps0.83Ts0.5Ts0.125Ts因此可得PID控制器有一个位于原点的极点和两个左半平面的零点11PIDpdiGKTsTs24()10.6(10.125)0.0750.5spsspssssTKTsKTTss454例：控制对象方程为，试用临界增益法确定PID控制器参数Kp,Ti,Td使得超调量不超过25%。如超调量过大则微调。1(1)(5)sss解：令，得到,0idTT()()(1)(5)ppKCsRssssK32650psssK系统特征方程为利用劳斯判据3210156306pppssKKssK可知临界增益为Kps＝30455将Kps代入特征方程，令s＝jw，得到32()6()5()0pjjjK226(5)(5)0j522.81sT查表得0.62.810.51.4050.1250.35ppsisdsKKTTTT216.3(1.42)1PIDpdisGKTsTss4560C(t)1t0C(t)1t系统的阶跃响应如右图所示。可见其超调量很大，经计算接近72%。要降低超调量，应使PID带来的零点进行调整，如果将s＝-1.42调至s＝-0.6，得到211810.833.315(0.6)PIDGssss可以计算出超调量在20%左右第六章采样系统分析6.1引言6.2信号的采样与保持6.3Z变换理论6.4采样系统的脉冲传递函数6.5采样系统分析由于进出数字计算机的信号都是断续的数字信号，因此，必须将原来的连续信号变成断续的信号，及采样信号。这样的控制系统必然在一处或几处出现脉冲信号或离散信号，这类系统称为采样控制系统。4586.16.1引言引言由于电子计算机进入自动控制领域，出现了数字计算机控制由于电子计算机进入自动控制领域，出现了数字计算机控制系统。可以说计算机与自动控制的结合，使自动化技术进入系统。可以说计算机与自动控制的结合，使自动化技术进入了崭新的前所未有的发展阶段。了崭新的前所未有的发展阶段。出入数字计算机的信号都是断续的数字信号，故必须将原来出入数字计算机的信号都是断续的数字信号，故必须将原来的连续信号变成断续信号，即采样信号。从某种意义上理解，的连续信号变成断续信号，即采样信号。从某种意义上理解，采样信号具有人为的性质。采样信号具有人为的性质。这样的控制系统必然在某一处或这样的控制系统必然在某一处或几处出现脉冲信号或数码信号，通常称之为采样控制系统。几处出现脉冲信号或数码信号，通常称之为采样控制系统。采样控制系统由于其控制对象本身是连续信号部采样控制系统由于其控制对象本身是连续信号部件，件，因而它因而它与离散系统有所区别；又由于其输出信号及控制作用的给定与离散系统有所区别；又由于其输出信号及控制作用的给定都是以数码形式出现的，因而它又与连续系统有所区别。都是以数码形式出现的，因而它又与连续系统有所区别。459总的来说，采样系统的分析与设计是按离散系统的方法总的来说，采样系统的分析与设计是按离散系统的方法来处理的，所以常常把它归结为离散系统。来处理的，所以常常把它归结为离散系统。严格地说，这两者是有区别的，主要表现在采样信号与严格地说，这两者是有区别的，主要表现在采样信号与离散信号的描述上。采样信号（或函数）是在整个实数离散信号的描述上。采样信号（或函数）是在整个实数轴上取值，其定义域是一维数集，而离散信号（或函轴上取值，其定义域是一维数集，而离散信号（或函数）则是实数轴上取正整数，其定义域是孤立点集。离数）则是实数轴上取正整数，其定义域是孤立点集。离散信号是一类客观存在的信号，如雷达系统中的脉冲序散信号是一类客观存在的信号，如雷达系统中的脉冲序列信号，数字系统中的二进制数码以及电报信号等，而列信号，数字系统中的二进制数码以及电报信号等，而采样信号是连续信号经采样器采样后人为地得到的，其采样信号是连续信号经采样器采样后人为地得到的，其周期可视实际需要而定。周期可视实际需要而定。4606.2信号的采样与保持6.2.1.采样过程如图所示计算机控制系统，被控对象是在连续信号作用下工作的，其控制信号、输出信号c(t)及其反馈信号、参考输入信号r(t)等均为连续信号，而计算机的输入、输出信号是离散的数字信号。DA/)(tr)(tc数字计算机)(tfAD/)(te)(kTe)(kTu)(1tu被控对象反馈装置图6.1计算机控制系统框图461由于计算机处理的是二进制的数椐，其输入信号不能是连续信号，所以误差信号要经过模/数转换器（A/D）变成计算机能接受的数字信号。这种将连续信号变为离散信号的过程称为采样。实际采样装置是多种多样的，但无论其具体实现如何，其基本功能可以用一个开关来表示，通常称为采样开关。连续信号加在采样开关一端，采样开关以一定规律开闭，另一端便得到离散信号。采样开关每次闭合时间极短，可以认为是瞬间完成。这样开关闭合一次，就认为得到连续信号的某一时刻的值。这样的采样开关称为理想采样开关，以后所说的采样开关都是指理想采样开关，简称为采样开关。462如果采样开关是等时间间隔采样，则称为普通采样、均匀采样、周期采样等。采样间隔时间称为采样周期，常用T表示。如果采样的时间间隔是时变的，则称为非周期采样、非均匀采样等。如果采样开关采样的时间间隔是随机的，则称为随机采样。一个离散系统中往往存在多个采样开关。如果系统中所有采样开关同时采样，则称为同步采样，否则称为非同步采样。如果所有采样开关都是均匀采样，但采样周期不等，则称为多速采样。•信号的采样过程：通过采样开关将连续信号离散化，转变为脉冲序列信号；•信号的保持过程：通过信号保持器将离散信号连续化；•两者互为逆过程；463采样和采样器将连续信号变为离散信号（脉冲序列）的过程称为采样；实现采样的装置称为采样器。采样器是离散系统的基本元件，每隔一段时间，开关闭合一次，使输入信号通过。采样过程脉冲调制器载波器Te(t)e(t)e(t)e(t)载波信号采样开关464有关概念有关概念A/DD/A数字控制器被控对象测量元件e(t)数字计算机r(t)e(t)u(t)uh(t)c(t)_计算机控制系统典型原理图2.离散系统：系统中有一处或多处为离散信号的系统称离散系统。典型的计算机控制系统即为离散系统的一种。其原理图如下：A/D：模数转换器，将连续的模拟信号转换为离散的数字信号。包括采样与量化两过程。1.离散信号：仅定义在离散时间上的信号称离散信号，离散信号以脉冲或数码的形式呈现。D/A：数模转换器，将离散的数字信号转换为连续的模拟信号。包括解码与复现两过程。465离散控制系统的特点–结构简单、控制灵活–检测器精度可以做得很高，则控制精度高–抗干扰性好：除非扰动和离散信号同时出现才会受到干扰–便于远距离传递。4666.2.2采样信号的数学描述1、几点假定（理想化）采样开关应能立即开或闭；通过采样开关的输出不发生畸变；采样时间(即采样装置闭合的时间)τ远小于采样周期T，分析时可以近似认为趋近于零；开关闭合时，其输出为常数；等采样周期，即采样周期T为常数。2、单位脉冲函数为单位脉冲函数，脉冲的宽度为无限小、幅度为无限大，而面积为1。0001)(ttt)(t1000()tttt或0t1467kTkTtTttkTtt)()()()()(…………-2T-T0T2T单位脉冲序列函数3、单位脉冲序列函数下式为单位脉冲序列函数，它是单位脉冲函数的序列。4、断续信号(采样信号）将连续的信号经采样后得到断续信号，利用单位脉冲序列函数可以描述断续信号为：kkTttete)()()(4681该过程可以看成是一个信号的调制过程，如图6-2所示，其中载波信号)(tpT是一个周期为T，宽度为（），的脉冲序列，如图6-2（b）所示。幅值为幅值正比于采样瞬时值的脉冲序列，如图6-2（c）所示。调制后得到的采样信号是一个周期为T，宽度为图6－2信号的采样过程实现上述采样过程的装置称为采样开关)()()(tftptf469•单位脉冲函数•单位脉冲函数的拉氏变换为1000()tttt或0()1stFstedt0t1t470拉氏变换的基本性质(6)位移定理：a.实域中的位移定理，若原函数在时间上延迟，则其象函数应乘以)()]([sFetfLsseb.复域中的位移定理，象函数的自变量延迟a，原函数应乘以，即)()]([asFtfeLatate471对于实际的采样控制系统，总有一个工作起始时间，因此假定当t<0时e(t)=0。则断续信号描述为（时域描述）0)()()(kkTttetee(t)e(t)0T2Tτ连续信号与采样信号注：)()0()()()()0()(TeeTtTetete对e(t)取拉氏变换，得00)()()()()(kkTskekTekTtkTeLteLsE上式可以将E(s)与离散时域信号e(kT)联系起来，可以直接看出e(t)的时间响应。但是e(t)仅描述了e(t)在采样时刻的值，所以E(s)不可能给出e(t)在两个采样时刻之间的任何信息。采样周期为T，则采样频率为，采样角频率为，但一般简称后者为采样频率。Tfs1Ts2472例6-1设e(t)=1(t)，试求e(t)的拉氏变换。【解】1,111)()(20TsTsTsTskkTseeeeekTesE例6-2设e(t)=e-at，t≥0，a为常数，试求e(t)的拉氏变换。【解】1eeeee11eeeekTesEasTaTTsTsasT0kaskT0kkTsakT0kkTs)()()(,)()(上例表明，用拉氏变换法来对离散信号进行变换时，得到的式子是有关s的超越函数，不利于分析。因此要引入z变换。473由于单位脉冲序列函数为周期函数，因此可以将其展开成傅里叶级数6.2.3采样信号的频谱分析kTkTtt)()(kTjkkTsect)(其中称为系统的采样频率。Ts2TdttTdtetTcttjkwTkTTs1)(1)(100022令则ktjkwsekTeT1te)()(ksjksET1sE)()(上式描述了采样过程的复频域特征。474如果连续信号e(t)的频谱E(j)是单一的连续频谱，则离散信号e(t)的频谱除包含原连续信号主频谱外（幅值为1/T），还包含无穷多个高频频谱。-wmax0wmaxE(jw)连续信号e(t)的频谱-ws-ws/2-wmax0wmaxws/2wsE(jw)w离散信号的频谱（smax)T2s4751.问题的提出连续信号e(t)经过采样后，只能给出采样点上的数值，不能知道各采样时刻之间的数值。从时域上看，采样过程损失了e(t)所含的信息。(a)连续信号t(b)离散信号t2.定性分析如果连续信号e(t)变化缓慢（最大角频率max较低〕，而采样角频率s比较高（即采样周期T=2/s较小〕，则e(t)基本上能反映e(t)的变化规律。怎样才能使采样信号e(t)大体上反映e(t)的变化规律呢？6.2.4采样定理476由于，则，所以。采样定理：为使离散信号不失真的还原成原来的连续信号，采样频率必须大于等于原连续信号所含最高频率的两倍。即max2smin21TTTs2minmax2T如果采样频率满足上面条件，则两相邻信号间无交叉部分。因此可设计如下理想滤波特性的滤波器，即可不失真地恢复原连续信号。2/,02/,1ssjG-ws/20ws/2wG(jw)理想滤波器的频率特性477注意：上述香农采样定理要求满足以下两个条件：（１）频谱的上限频率是有限的；（２）存在一个理想的低通滤波器。但可以证明理想的低通滤波器在物理上是不可实现的，在实际应用中只能用非理想的低通滤波器来代替理想的低通滤波器；478由于实际的非周期连续信号的频率特性中最高频率是无穷大的，因此离散信号频谱必然相互交叉，采样频率的选取发生困难，此时必须作近似处理：连续信号频谱特性的频带宽度（即当频率特性的幅值为零频幅值e(0)的5%时所对应的频率）为连续信号所含的最高频率。近似处理得到后，即可利用采样定理得到采样频率。max-wmax0wmaxwE(jw)E(0)0.05E(0)非周期连续信号的频谱479例6-3设e(t)=e-t，试按采样定理选择采样频率。【解】首先求连续信号的拉氏变换11ssE其频率特性为幅频特性为11jjE112jE若在处截断，可求频带宽度为005.0EjE则由采样定理可求得采样频率max2/20,05.011sradbbsrads/402max480讨论信号的复现，首先从研究采样信号的频谱特性讨论信号的复现，首先从研究采样信号的频谱特性入手。为此，需要找出与之间的相互入手。为此，需要找出与之间的相互联系。经过简单的数学分析，找出了它们之间的关联系。经过简单的数学分析，找出了它们之间的关系式为系式为或或Es()ksT1)jks(E)s(EEt()6.2.5信号的保持ksT1)jkj(E)j(E采样控制系统中的被控制对象，执行通常都是一些采样控制系统中的被控制对象，执行通常都是一些模拟部件，如执行电机，液压舵机等。它们都是靠模拟部件，如执行电机，液压舵机等。它们都是靠模拟信号工作的。这样就需要将采样信号变成连续模拟信号工作的。这样就需要将采样信号变成连续信号。信号。481一般说来，信号经采样得到采样信号，一般说来，信号经采样得到采样信号，在信息上是有丢失的，造成了信号的失真。在什么条件下在信息上是有丢失的，造成了信号的失真。在什么条件下不能保证信息不失去，又能将采样信号恢复成连续信号？不能保证信息不失去，又能将采样信号恢复成连续信号？香农采样定理告诉我们，要从采样信号中完全复现出采样香农采样定理告诉我们，要从采样信号中完全复现出采样前的连续信号，必须满足采样频率大于或等于两前的连续信号，必须满足采样频率大于或等于两倍输入连续信号频谱中的最高频率，倍输入连续信号频谱中的最高频率，即即在满足在满足ShannonShannon定理的条件下，要想不失真地重复采样定理的条件下，要想不失真地重复采样器的输入信号，还需要一种理想的低通滤波器。器的输入信号，还需要一种理想的低通滤波器。et()et()et()et()maxmax2s482连续信号经过采样后生成的断续信号频谱中除了主频谱分量外，还产生了无穷多附加频谱分量，这些分量在系统中相当于高频干扰信号。为除去高频分量对系统输出的影响，恢复和重现原来的连续输入信号，需要应用低通滤波器。通常用来起低通滤波器作用的为各阶保持电路或保持器，例如零阶保持器和一阶保持器。保持器的作用是将采样信号转换为连续信号，这个连续信号近似的重现作用在采样器上的信号。483零阶保持器能将采样信号转变成在两个连续采样时刻之间保持常量的信号，即在区间内，零阶保持器的输出值一直保持为x(nT)。如下图所示。零阶保持器的输出xb(t)为阶梯信号。因为在每个采样区间的值均为常数，其导数为零，故称为零阶保持器。TnnTt)1(,原连续信号零阶保持器的恢复信号x(t)Gh(s)x(t)采样开关保持器xh(t)零阶保持器484零阶保持器的传递函数考察保持器的输出xh(t)与连续输入信号x(t)之间的关系。0))(1)(1)(()(khTkTtkTtkTxtxTssxkkTshessekTxsx11)()()(0)(1)()(sGsesxsxhTsh将上面结果求拉氏变换，得从而可以得到保持器的输出xh(t)与断续输入信号x(t)之比，即零阶保持器的传递函数为485当时，。零阶保持器的频率特征用代替Gh(S)中的s，得零阶保持器的频率特性jje1jGTjh)(jeeeTjTjTj212121)(jeexjxjx2sin)sin(Te221Tj21Tj2T2Th21eTjG)sin()(当很小近似为0时，，22sinTTTjGh)(s02sin2sin2ssTs0)(jGhsnn只要是的整数倍，则，相频特性为:486零阶保持器的幅频特征和相频特性如下图所示。487由于幅频特性的幅值随频率的增加而衰减，零阶保持器是一个低通滤波器，但不是一个理想滤波器。它除了允许的主要频谱分量通过以外，还通过一部分高频分量，从而造成数字控制系统的输出中存在纹波。另外，从相频特性还可以看到，零阶保持器还会产生负相移（滞后相移），因此，零阶保持器的引入，会导致稳定性变差。除了零阶保持器外（步进电机，DA转换器等），还有一阶、二阶等高阶保持器。由于他们实现起来比较复杂，而且相角滞后比零阶保持器更大。4886.3.1ZZ变换的定义变换的定义拉普拉斯变换（又称L变换）和傅里叶变换（又称F变换）等积分变换，在微分方程求解中获得了广泛的应用。线性常系数微分方程通过L变换变成代数方程，从而使求解微分方程得到简化。因此，拉普拉斯变换与傅里叶变换是分析线性连续系统的主要工具。事实上，Z变换的历史比较古老，其基本思想是18世纪英国数学家德﹒莫费（DeMoivre）在概率论的研究中首次提出的。从19世纪的拉普拉斯至20世纪的沙尔（HLSeal﹒﹒），其间许多人在这方面都作出了贡献。然而，在那样一个较为局限的数学领域中，Z变换理论没有得到充分的运用和发展，直到本世纪50年代以后，计算机控制系统的迅速发展，为Z变换的研究与应用开辟了广阔的天地6.3z6.3z变换变换489连续信号经采样后得到的脉冲序列为)(tf0)()()(kkTtkTftf0)()(kkTsekTfsF对上式进行Laplace变换，得490由于采样信号的拉氏变换是s的超越函数，出现指数项，无法得到象线性连续系统中那样的特征方程为线性代数方程。z变换将复平面问题转化为Z平面上的问题：采样信号的拉氏变换为s平面：kTse0)()(kkTsekTxsX引入变量，，则得z变换的定义式：TsezzT1sln0kkzkTxzX)()(z平面：由此可看出是关于复变量的幂级数。...)()()()(210zT2xzTxz0xzX1z)(zX491几点说明1)在控制工程中，离散信号x(t)通常由对连续信号x(t)采样得到，所以习惯上称X(z)是x(t)的Z变换，但实际上是指x(t)经采样后得到的离散信号x(s)的Z变换。同样，习惯上也称X(z)是X(s)的Z变换，本书中也这样称呼，不再作说明；2)X(s)是x(t)的L变换的记号，X(z)是{x(kT)}的Z变换的记号，切不要以为X(z)是中的s用z代替后的式子，即X(z)≠X(s)s=z；3)连续函数x(t)的L变换定义式dtetxtxLsX0st)()]([)(x(t)的z变换记为Z[x(t)]，Z[x(t)]=0kkzkTxzX)()(4926.3.2z变换表达式的求法1、级数求和法知道连续函数x(t)在各采样时刻的离散值x(t)，按定义求。例6-4求和的Z变换表达式。【解】)()(t1tx102)()(kkTttx0k121k111zzz11zz1zkTxzX)()(0k21k221zzzz1zkTxzX)()(由该例可知，在z变换中只考虑采样时刻的信号值，因此连续信号与采样后的断续信号的z变换结果相同。求采样信号的求采样信号的ZZ变换方法很多，常用的方法有：变换方法很多，常用的方法有：按定义求，部分分式法，留数计算法。按定义求，部分分式法，留数计算法。493例6-5求的Z变换表达式。ttx)(3210kk0kkTz3Tz2TzkTzzkTxtxZzX)()()()()(121111211z1zz1zz11Tzz3z21Tz1z111z1Tz122111zTzz1Tz)()(494练习：求指数函数的z变换。解：设，则kakTTaaTzezezezF2211)()(,111aTaTaTezezzzeatetf)(atetf)(4952部分分式法①先求出已知连续时间函数e(t)的拉氏变换E(s)；②将E(s)展开成部分分式之和的形式；③求拉氏反变换，再求Z变换E(z)。496例6-6设，求的z变换。)1(1)(sssF)(tf解：上式两边求Laplace反变换，得)0(,1)(tetft再由例6-4和练习有111)(sssF))(()(])([)(TTTtez1ze1zezz1zzet1zzF497练习已知求Z变换表达式。assasG)(aTaTaTez1zze1ezz1zzas1s1ZzG)(4983.查表法把常用的函数及其Z变换列成对照表，求取Z变换时，直接查表。这种方法在实际工作中非常简单有用。书中给出了一张比较详细的Z变换表。当然，不可能所有函数的Z变换式都能在表中直接查到。在查表时，首先对所求函数作一些变化，以适合Z变换表。例如，进行部分分式展开，或应用Z变换基本定理等。499常用普通时间函数的常用普通时间函数的ZZ变换见表变换见表6-6-1(p.141)1(p.141)表表6-16-1ZZ变换表变换表5005016.3.3z变换的性质1、线性定理)(.......)()](......)([1111zXazXatxatxaZnnnn其中a1,a2……an为常数。证明：112211220[()()][()()]kkZaftaftafkTafkTz022011)()(kkkkzkTfazkTfa)()(2211zFazFa5022、时域位移定理10)()()(mkkmzkTxzXzmTtxZ)()(zXzmTtxZm向前差分定理向后差分定理注向后差分定理仅在k<0时，X(kT)=0的情况下才成立。503证明：由Z变换定义式有：0)()(kmmkzzzmTkTxmTtxZ])()()([1010mkkmkkmkkmzkTxzkTxzkTxz])()([10mkkmzkTxzXz0)()(kkzmTkTxmTtxZ0)(kmmkzzzmkx0)()(kmkmzmkxzmkkmzkxz'')(')(zXzm由于k<0时，X(kT)=0504若，则3、复域位移定理)()(zeXtxeZaTat)()(zXtxZ证明0)()]([kkTsakTatekTxetxeZ0)(kakTkTsekTx0)()(kaskTekTx)()(202zeXzXzkTxaTkkzeezaTaTTs2现令Tsez由于5054、微分定理)()(zXdzdTzttxZ若，则)()(zXtxZ证明NkkNzkTxdzdTzzXdzdTz0)(lim)(10)()(limkNkNzkkTxTzNkkNzkTkTx0)(lim)(ttxZ【例】已知，求Z变换表达式。【解】由于3)(ttx3221z1zzTtZ)()()(])()([3231z1zzTdzdTztZ423)1()14(zzzzT5065、初值定理)(lim)0(zXxz0)()(kkzkTxzX)0()()0(lim)(lim1xzTxxzXzz用于分析过渡过程，即原函数的0值等于z变换函数时的极限。z证明6、终值定理)()1(lim)()1(lim)(111zXzzXzxzz0)()(kkzkTxzX)0()()1()(0xzXzzTkXTtxZkk)0()()1()()1(0zxzXzzkTxTkxkk证明0)()0()(1lim1xxzxzXzz507设x(nT)和y(nT)为两个采样函数，其离散卷积定义为x(nT)y(nT)=，则卷积定理为：Z[x(nT)y(nT)]=X(z)Y(z)0])[()(kTknykTx7.卷积定理8.乘以指数序列性质若若a为整数，则为整数，则9.比例尺变换性质若若则则ZxnTXz[()]()1nZaxnTXaz[()]()ZxnTXz[()]()1/aZxanTXz[()]()5086.3.4z反变换Z变换将分析差分方程的问题转换为分析代数方程问题，然后通过求x(z)的原函数，可求出离散系统的时域响应。这就是z反变换。1、幂级数法：（长除法）Z变换函数，通常可表示为两个Z的多项式之比，一般可写成：在实际情况下，。用分母除分子，并将商按的升幂排列得：)()(11011nmazazbzbzbzXnnnmmmmmn1z00110)(kkkkkkkzkTxzczczcczX)()()()(10kTtcTtctctxk则5092、部分分式法部分分式法又称为查表法，其基本思想是将X(z)/z展开成部分分式，niiizzAzzX1)()(kTx然后查z变换表，即可求得原函数。这种方法的依据是这种方法的依据是ZZ变换的小线性性质，变换的小线性性质，ZZ变换式变换式通常是通常是zz的有理分式。只要将的有理分式展开的有理分式。只要将的有理分式展开为部分分式，逐项查为部分分式，逐项查ZZ变换表，就可以得到反变换式。变换表，就可以得到反变换式。这里与拉氏变换不同的是，这里与拉氏变换不同的是，不是直接将展开，不是直接将展开，而是将展开而是将展开，道理是，在，道理是，在ZZ变换表上，基本变换表上，基本变换式中普遍含有因子变换式中普遍含有因子zz，因此，若展开，，因此，若展开，即把中的因式即把中的因式zz提出来，可保证分解后的各个分提出来，可保证分解后的各个分式都含有式都含有zz因子。因子。Xz()Xz()Xz()Xz()/Xzz()/Xzz()510设设先求出的特征根，即将其分母分解因式，形如：先求出的特征根，即将其分母分解因式，形如：在工程上，多有极点都是一阶极点的情况，即分母多项在工程上，多有极点都是一阶极点的情况，即分母多项式中无重根时，上式则可化为：式中无重根时，上式则可化为：其中系数其中系数,,可由式决定：可由式决定：10111011mmmmnnnnbzbzbzbXzazazaza()101101mmmmniibzbzbzbXzazz()()Xz()1212nnAAAXzzzzzzzz()()iAiiizzXzAzzz()()511例6-7已知z变换函数求其z反变换。))(1()(TezzzzF解：首先将展成部分分式TezKzKzzF211)(TzezFzzK11)(1lim11zzF)(TTezezFzezKT11)(lim2TTezzzzezF111)(nTTeenTf111)(0)()1(11)(kkTTkTteetf5123、留数法：又称反演积分法。–由z变换的定义可知0)()(kkzkTfzFdzzkTfdzzzFkkmm011)()(dzzkTfdzzzFkmkm101)()(011)()(kkmmzkTfzzF1)(kzzF包围了的所有极点513)()()!1(1lim)(111)1(zxzzzdzdrzxzReskrirrzzki其中Res[]表示函数的留数。例6-8已知z变换函数为试用围线积分方法求z反变换。)2)(1(10)(zzzzF设的极点为，则1)(kzzFnizi,,2,1,niikzzzFreskTf11],)([)(514解：•上式有两个极点和，且)2)(1(10)(1zzzzzFkk10)()1(lim]1,)([111kzkzzFzzzFreskkzkzzFzzzFres210)()2(lim]2,)([121)12(10)(kkTf),2,1,0(k所以11z22z515)(zXxnT())(txz反变换是z变换的逆运算。其目的是由象函数求出所对应的采样脉冲序列（或），记作z反变换只能给出采样信号，而不能给出连续信号x(t)。注意1ZXzxnT[()]())(tx516）三种）三种zz反变换法的比较反变换法的比较分分式法分分式法通过通过ZZ变换表变换表66--11可方便地求得可方便地求得,,留数留数算法算法可以直接求出序列，因而容易求得。可以直接求出序列，因而容易求得。这两种方法有一个共同的特点，都需要知道这两种方法有一个共同的特点，都需要知道的全部极点的全部极点,,这意味着要求解高阶代数方程，这意味着要求解高阶代数方程，是一件困难的事，因此在应用上有一定的局限性，是一件困难的事，因此在应用上有一定的局限性，般不宜用于高阶采样系统。般不宜用于高阶采样系统。长除法长除法却没有这种限制，通用性好。它的缺点是却没有这种限制，通用性好。它的缺点是算起来麻烦，而且往往得不到闭合的表示形式。算起来麻烦，而且往往得不到闭合的表示形式。xnT()Xz()xt()xt()517作业P1596-55186.46.4采样系统的脉冲传递函数采样系统的脉冲传递函数脉冲传递函数的定义及意义串联环节的脉冲传递函数闭环脉冲传递函数5196.4.16.4.1脉冲传递函数脉冲传递函数1、脉冲传递函数的定义及意义脉冲传递函数是在零初始条件下，输出采样信号的Z变换与输入采样信号的Z变换之比，即：G(z)=C(z)/R(z)。要注意的是要注意的是：：输出端是连续信号，此时要在其输出端虚设一个理想同步采输出端是连续信号，此时要在其输出端虚设一个理想同步采样开。样开。所谓零初始条件，是指所谓零初始条件，是指tt<0<0时，输入输出的采样值均为零。时，输入输出的采样值均为零。图8－1520Gs()Rs()Cs()Gz()TT521在实际中，只讨论在采样时刻输出与输入采样信号间的关系。)(tx)(tx)(th)(sG)(ty0)()()(nnTtnTxtx)()()()()()0()(nTtnTxTtTxtxtx])[()(])1[()()()0()(TnkhnTxTkhTxkThxkTy0])[()(nTnkhnTx][)(][)()()()(nTthnTxTthTxth0xty5220])[()()(nTnkhnTxkTy0)()(kkzkTyzY00])[()(knkzTnkhnTx0)(0])[()(knknnzTnkhznTx00)()(])[()()()(jjknkzjThzTnkhzXzYzG)]([)(sGZzG可见,采样系统的脉冲传递函数是连续系统脉冲响应h(t)的采样序列的Z变换,也可以说G(Z)是h(t)或G(S)的Z变换，即G(Z)=Z[h(T)]=Z[G(S)]523脉冲传递函数的一般步骤脉冲传递函数的一般步骤得连续部分的传递函数得连续部分的传递函数;;得连续部分的脉冲瞬间响应得连续部分的脉冲瞬间响应得采样的脉冲传递函数的得采样的脉冲传递函数的ZZ变换变换Gs()Gz())()(sGLth1)(th524求该开环系统的脉冲传递函数。例6-9系统结构如图所示，其中连续部分的传递函数为)11.0(1)(sssG)(zG525解：•连续部分的脉冲响应函数为)0()1()(10tetgtkTekTg101)(0)()(kkzkTgzG0101kkkTzeTezzzz101))(1()1(1010TTezzez脉冲传递函数为526或由得)(sG1011)(sssG))(1()1(1)(101010TTTezzezezzzzzG查表得5272、串联环节的脉冲传递函数两个环节串联，有两种方式，一种是串联环节之间没有采样开关，一种是串联环节之间有采样开关，其总的脉冲传递函数有所不同。（1）、串联环节之间没有采样开关此时，)()()(21sGsGsG)()(2121zGGsGsGZzG528例6-10系统结构如图6-11所示，其中求开环脉冲传递函数。assG1)(1bssG1)(2图6-11529解：bsasabsGsG111)()(2112()()1()()()aTbTaTbTGzGGzzeebazeze530（2）、串联环节之间有采样开关此时，假设采样开关是同步采样。)()()(1zXzGzD)()()()()()(212zRzGzGzDzGzY)()()(21zGzGzGd(t)r(t)注)()()(2121zGGzGzG图6－12531例8-12已知，，求脉冲传递函数。【解】ssG1)(11010)(2ssG))(1()1(])10(10[)()(101021TTezzezssZzGGzG]1010[]1[)()()(21sZsZzGzGzG))(1(1010110210TTezzzezzzz若无采样开关，则若有采样开关，则注：此两环节不同，虽然极点相同，但零点不同。532练习：系统结构如图6-12所示，其中求开环脉冲传递函数。1211(),()GsGssasb533（3）有零阶保持器时的脉冲传递函数开环脉冲传递函数为图6-13带零阶保持器的开环采样系统)()]()(1[)()](1[)(000zRsGsesGsZzRsGseZzCTsTs)(])([)1()(01zRssGZzzC])([)1()()()(01ssGZzzRzCzGssGZzsGseZ010Ts)()(534例6-14系统结构如图6-13所示，其中采样周期秒•求其开环脉冲传递函数。)1()(ssKsG1T0535解：•由于•所以1111)(12sssKsGs1211)1(]1[)(ezzzzzzzKzG)368.0)(1()717.0(368.0))(1()21(111zzzKezzezeK05364、闭环脉冲传函537（1）、输出对输入的脉冲传函令0d)()()()()()()()()()()()(zHGG1zRzEzEzHGGzBzBzRzEzEzGGzY212121)()()()(zHGG1zRzGGzY2121)(1)()()()(2121zHGGzGGzRzYz)(11)()()(21zHGGzRzEzGe数为其中，误差脉冲传递函538在上述推导中应特别注意的是,作为输入信号的R(s)不能用采样信号代替。因为，对一个系统连续输入信号的响应和离散输入信号的响应是截然不同的，而作为输出信号的c(t)或C(s),可以只研究其采样时刻的值,所以能对它进行采样。这一点必须认识清楚,否则会得到错误结果。539（2）、输出对扰动的脉冲传函令0)(tr)()()()()(212zEzGGzDzGzY)]()()()([)(212zEzHGGzDzHGzE)()(1)()(212zDzHGGzHGzE)()(1)()()()()(212212zDzHGGzHGzGGzDzGzYE(z)由两部分组成，D(z)通过G2(z)产生一部分，E(z)回路本身的产生一部分。)(1)()()()()()(212212zHGGzHGzGGzGzDzYzd540注在求解复杂离散系统的脉冲传递函数时，由于采样开关处在不同的位置，即使各动态环节的传递函数相同，脉冲传递函数也可能不同。有时采样开关的位置可能导致无法求出脉冲传函，而只能求出输出z变换表达式。如果从输入到输出的直接通道均无采样开关，则不可能写出闭环脉冲传函。541)()()()()()(sCsHsGsRsGsC)()()()(zCzGHzGRzC)(1)()(zGHzGRzC误差点没有采样开关的闭环采样系统此系统不存在闭环脉冲传递函数。542【例】已知采样系统结构如下图示，求系统输出Z变换的表达式。)()()()(zBzGzGRzY)()()()(zBzGHzGHRzB)()()(zGH1zGHRzB)()()()()(zGH1zGHRzGzGRzY【解】无法求取闭环脉冲函数。543【例】已知离散系统结构如下图示，当T=0.1时，求系统的单位阶跃响应。【解】TezzzssZzG101212])11.0(2[)(368.0368.1264.1)368.0)(1(736.022zzzzzzz368.0104.0264.1)(1)()(2zzzzGzGz1)()()()(zzzGzXzGzYBB4321849.0945.0396.1264.1zzzz)2.0(396.1)1.0(264.1)(ttty544表表8-28-2闭环采样系统的典型结构图闭环采样系统的典型结构图5455466.56.5采样控制系统分析采样控制系统分析稳定性分析瞬态响应稳态误差分析5476.5.16.5.1线性采样系统的稳定性线性采样系统的稳定性（（11）一般概念）一般概念稳定性是指线性采样系统的重要问题，一个系统只有稳定稳定性是指线性采样系统的重要问题，一个系统只有稳定才能正常工作。才能正常工作。在线性连续系统的分析中，我们曾经指出，稳定系统的特在线性连续系统的分析中，我们曾经指出，稳定系统的特征方程的根全部位于征方程的根全部位于ss平面的左半部。这一概念也适用于平面的左半部。这一概念也适用于线性采样系统。线性采样系统。线性采样系统特征方程可以令脉冲传递函数的分母为零而线性采样系统特征方程可以令脉冲传递函数的分母为零而得到，特征方程根的位置就确定了系统是否稳定得到，特征方程根的位置就确定了系统是否稳定。为了。为了在在zz平面上讨论线性采样系统的稳定性，我们必须知道平面上讨论线性采样系统的稳定性，我们必须知道ss平面和平面和zz平面的对应关系。平面的对应关系。548））ss平面与平面与zz平面的映射关系平面的映射关系变换中定义：，设则变换中定义：，设则，得，得就有如下图所示的就有如下图所示的ss平面与平面与zz平面的映射关系平面的映射关系sTzesjTezzT010101zzz549分析：离散系统的特征方程实际上是将s平面的信息，通过z变换转移到了z平面。考察TjTjTTseeeez)(1ez01z01e1z0TT0Re[S]ImReIm[Z]1-1线性离散控制系统稳定的充要条件：线性离散闭环控制系统特征方程的根的模小于1，则系统是稳定的。线性离散闭环控制系统脉冲传递函数为则其特征方程为zGzGz101zG550例6-14已知离散系统结构如下图示，当T=1时，分析稳定性。【解】)368.0)(1(32.6])1(10[)(zzzssZzG0368.0952.40)(12zzzG876.4076.021zz12z所以系统不稳定。551劳斯稳定判据•在分析连续系统分析连续系统时，曾应用Routh稳定判据判断系统的特征根位于s右半平面的个数，并依此来判断系统的稳定性。•对于采样系统采样系统，也可用Routh判据分析其稳定性，但由于在z域中稳定区域是单位圆内，而不是左半平面，因此不能直接应用Routh判据。552代数稳定性判据劳斯代数判据无法直接应用在z平面上，因此引入双线性映射,将z平面的点映射到w平面上研究。假定z平面上一点对应w平面上一点jyxzjvuw11z222222)1(2)1(1)(yxyjyxyxjvu2222)1(1yxyxu令jyxjyxzzw)1()1(11553对Z平面上的一点，设在单位圆上，，则u=0，对应W平面上的虚轴。对Z平面上单位圆内点，对应，则u<0，对应W平面上的左半平面，为系统的稳定域。对Z平面上单位圆外点，对应，则对应W平面上的右半平面，为系统的不稳定域。因此可在W平面上利用劳斯代数判据分析采样系统的稳定性。122yx122yx122yx0Re[W]ImReIm[Z]1-1554例6-15已知离散系统结构如下图示，当T=0.1时，分析稳定性。【解】).)(.()(1s0501s10s2Zz1zzG2T20T102ezz10ezz401zz401zz30z1z..)(..0)(1zG005350z33560z0011z23...11wwz0340w651w683w33223....340w0431w340683w651332w023......劳斯表中第一列为正，系统稳定。555稳定性判据Tse][s][z][wTsez11wwz556sTze11zwz557）判稳方法）判稳方法该系统稳定的充分必要条件为：该系统稳定的充分必要条件为：系统闭环特征方系统闭环特征方的根的根（）（）均分布在均分布在zz平面上以原平面上以原为中心的单位圆内，即为中心的单位圆内，即（（推广的劳斯稳定判据：在线性采样系统中，对推广的劳斯稳定判据：在线性采样系统中，对zz有理多项式，经的双线性变换，得到有理多项式，经的双线性变换，得到ww代数方程就可以应用劳斯判据判稳了。为了区别代数方程就可以应用劳斯判据判稳了。为了区别面下的劳斯判据，称面下的劳斯判据，称ww平面下的劳斯判据为推广平面下的劳斯判据为推广劳斯稳定判据。劳斯稳定判据。iz1i，2，3，1iz1i，2，3，11wzw558连续系统，，则系统稳定；离散系统，，则系统稳定。例6-16当T=0.1时，分析稳定性。求使系统稳定的K取值范围。【解】368.0368.1632.0)11.0()(2zzkzsskZzG0)(1zG0368.0)368.1632.0(2zkz11wwz0632.0736.2264.1632.02kwkw334k0.k0559令由【例】已知系统结构如图，分析稳定性与采样周期的关系。【解】)1(11)(2ssZzzzGTTTTTezezTeezeT)1(1)1(211TTeea0)(1zG01)2(2TazTz11wwz042)(2TaTaTwwTaT04TaT2140aT令得560作业P1597,10(1,2)561562一般假定外作用为单位阶跃函数r(t)=1(t)，此时R(z)=z/(z-1)，则系统输出量的Z变换函数为时间响应1)()(zzzzC然后用长除法，将C(z)展成无穷幂级数：C(z)=C0+C1z-1+C2z-2+…+Cnz-n在C(t)—t坐标中描出点(kT,Ck),k=0,1,2,…n，则得阶跃响应脉冲序列。则得单位阶跃作用下的输出序列为C(kT)=Ck,k=0,1,2,…n将各点用虚线平滑连接，以便分析性能指标。6.5.2采样系统的瞬态响应563ccicic0c0zcizc0cic0ci564若，即闭环极点位于右半z平面的圆周上，则闭环系统瞬态响应为等幅脉冲。若，即闭环极点位于单位圆内，则输出响应呈指数衰减。若，即闭环极点位于单位圆外，则输出响应呈指数增长，发散。令，则下面分析闭环极点对瞬态响应的影响。1、为正实根，则对应的瞬态分量kpnkkkkkpcpzzcZnty)(11kp1kpkatkpT1aepln,anTkkecnty1kp5655662、为负实根，则对应的瞬态分量kp若，即闭环极点位于左半z平面的圆周上，则闭环系统瞬态响应为等幅跳跃输出。若，即闭环极点位于左半z平面的单位圆内，则输出响应呈指数交叉跳跃衰减。若，即闭环极点位于左半z平面的单位圆外，则输出响应呈指数交叉跳跃增长，发散。1kp1kp1kpnkkkk1kpcpzzcZnty)(567若，则对应的瞬态响应为振幅衰减的余弦震荡。若，则对应的瞬态响应为发散的余弦震荡。和也为一对共轭复数，3、和为一对共轭复根，即kp1kpkkjk1kjkkeppeppkkjnnk1kjnnkk1kkepcepcy,kc1kckkjkkjkkeccecc1)()(,kkkknjnkknjnkk1kkepcepcy)cos(kknkknpc21kp1kp568闭环复极点分布与相应的动态响应形式闭环复极点分布与相应的动态响应形式闭环复极点分布与相应的动态响应形式569稳态性能是系统重要性能指标之一，通常用稳态误差表稳态性能是系统重要性能指标之一，通常用稳态误差表示。下面讨论一下稳态误差的求法。示。下面讨论一下稳态误差的求法。（（11）通过查响应曲线）通过查响应曲线根据线性采样系统的响应曲线或响应误差曲线根据线性采样系统的响应曲线或响应误差曲线，然后在情况下，由与，然后在情况下，由与的差值或直接由响应误差求取系统的稳态的差值或直接由响应误差求取系统的稳态误差。误差。这里为系统响应的过渡过程时间。注意：这里为系统响应的过渡过程时间。注意：是从开始计算，是误差变量对于是从开始计算，是误差变量对于tt的函数。的函数。在工程上，一般取（正好是采样点），或在工程上，一般取（正好是采样点），或tt略大于（不是采样点）的采样点，所对应的时间求略大于（不是采样点）的采样点，所对应的时间求稳态误差。稳态误差。ct()et()sttrt()ct()et()stsset()sttsttst6.5.3稳态误差分析570超调量C(t)C(t)上升时间tr峰值时间tp调节时间ts误差带误差带稳态误差稳态误差)(too1.01.0tt控制系统性能指标控制系统性能指标571（（22）应用终值定理求取）应用终值定理求取如图所示系统，如图所示系统，ee（（tt）为系统误差连续信号，）为系统误差连续信号，为系统采样信号，由终值定理可以求出线性采样系为系统采样信号，由终值定理可以求出线性采样系统的稳态误差为统的稳态误差为et()11limlim11lim1tzzeetzEzzRzGz()()()()()()()572如图所示的单位反馈的闭环离散系统的误差脉冲传递函数为)(11)(zGzGe)(1)()(zGzGzGB)(1)(zGzGBe系统误差)()(11)()()(zRzGzRzGzEe)(1)()1(lim)(1zGzRzez终值定理573与连续系统类似，根据系统开环脉冲传递函数在z=1的极点的个数，离散控制系统可分为0型、1型……系统。1、单位阶跃输入1)(11)1(lim)(1zzzGzez)(11lim1zGz)1(1Gkppke1)(定义位置误差系数则对0型系统对1型以上系统0)(,ekp574则G1中没有z=1的极点，，2、单位斜坡输入2)1()(zTzzR)()1(lim)1()(11)1(lim)(121zGzTzTzzGzezz)()1(lim11zGzTkzvvke1)(0vk)(e)1()()(1zzGzG)1(11GTkvvke1)(vk0)(e定义速度误差系数则对0型系统对1型系统，令对2型系统，575则对0型、1型系统3、抛物线输入则G1中没有z=1的极点，所以，2)(2ttr)()1(1lim)1(2)1()(11)1(lim)(212321zGzTzzzTzGzezz)()1(lim1212zGzTkzaake1)(0ak)(e21)1()()(zzGzG)1(112GTkaake1)(ak0)(e对2型系统，令对3型以上系统，定义加速度误差系数576稳态误差分析系统阶跃输入r(t)=1(t)斜坡输入r(t)=t抛物线输入r(t)=t2/20型1/kp∞∞1型01/kv∞2型001/ka577例6-17已知采样系统结构如图，求单位阶跃和单位斜坡输入时的系统误差。T=0.1s【解】)368.0)(1(264.1)11.0(2)(zzzssZzG如果输入为单位阶跃，因为系统为1型，故系统无误差。如果输入为单位斜坡时，0501zTzzG111ze21z.)()()(lim)(632026413680zz2641T1zGT1k1z11zv....lim)(lim05026416320k1ev...)(或者578例6-18已知采样系统的结构如图所示，其中，，采样周期秒，求在输入信号的作用下，系统的稳态误差。2)15.0(2)(sssG2.0T图6-21)0(,5.01)(2ttttr579解：3)15.0(21)(ssZzzzG322)1()1()1(1zzzTzTzzz2)1(16.024.0zz084.076.1)(2zzzD采样系统的闭环特征方程为采样系统的开环脉冲传递函数为580该采样系统稳定在阶跃和斜坡函数作用下的稳态误差为零静态加速度误差系数为08.0)16.024.0(lim)()1(lim121zzGzKzza5.008.004.00011)(2avpKTKTKe25.01)(tttr因此，在输入作用下的稳态误差为581第七章状态空间分析设计第七章状态空间分析设计在状态空间中以状态向量或状态变量描述系统的方法称为系统的状态空间模型（内部表达）。控制系统的两种基本描述方法：控制系统的两种基本描述方法：输入—输出描述法——经典控制理论状态空间描述法——现代控制理论经典控制理论的特点：经典控制理论的特点：(1)优点：对单入—单出系统的分析和综合特别有效。(2)缺点：内部的信息无法描述，仅适于单入—单出系统。现代控制理论现代控制理论(1)适应控制工程的高性能发展需要，于60年代提出。(2)可处理时变、非线性、多输入—多输出问题。(3)应用方面的理论分支：最优控制、系统辩识，自适应控制……582基本概念–状态：系统过去、现在和将来的状况。–状态变量：状态变量指能确定系统运动状态的最少数目的一组变量。–状态向量：若以n个状态变量做为向量的分量，则称为状态向量。–状态空间：以状态变量为基构成的n维空间。–状态方程：描述系统状态变量与输入变量之间关系的一阶微分方程组称为状态方程。–输出方程：系统输出量y(t)与状态变量、输入量的关系的表达式称为输出方程。()Xt12,,......,nxtxtxt()Xt12,,......,nxtxtxt5832.52.5状态空间模型（现代控制理论）状态空间模型（现代控制理论）定义在状态空间中以状态向量或状态变量描述系统的方法称为系统的状态空间模型（内部表达）。优点–能完全表达出系统的全部状态和性能（内部和外部）–能了解系统内部状态的变化特性–容易考虑初始条件–适用范围广:时变系统，非线性系统，多输入多输出–便于设计584状态方程的一般形式–单输入线性定常连续系统式中常系数与系统特性有关。上式可以写成向量矩阵形式：其中1111122112211222221122nnnnnnnnnnnxtaxtaxtxtbutxtaxtaxtxtbutxtaxtaxtxtbutaaa111,,;,,;nnnabba111112112221222212(),,,nnnnnnnnnxxaaabxxaaabxtxtAbxxaaabxtAxtbut585–多输入线性定常连续系统向量矩阵形式为：其中)()()(tButAxtx11111221111122122112222211222211221122nnppnnppnnnnnnnnnppxaxaxxbububuxaxaxxbububuxaxaxxbububuaaap21np2n1np22221p11211nn2n1nn22221n11211n21n21uuuubbbbabbbbaaaaaaaaaxxxxxxxx,B,A,,586输出方程：系统输出量与状态变量、输入量的关系称为输出方程。输出量由系统任务确定或给定–单输出线性定常连续系统输出方程的一般形式为式中常系数与系统特性有关。其向量矩阵形式为：–多输入－多输出系统的输出方程的一般形式为•其向量矩阵形式为：12,,ncccd；1112nnytcxtcxtcxtdutytcxtdutyCxDupqpqqnqnqqqppnnppnnudududxcxcxcyudududxcxcxcyudududxcxcxcy22112211222212122221212121211112121111587状态空间表达式：状态方程与输出方程的组合称为状态空间表达式，又称动态方程。–A(t):系统矩阵（状态矩阵）–B(t):控制矩阵（输入矩阵）–C(t):观测矩阵（输出矩阵）–D(t):直接传递矩阵xAxByCxDuuxAxbuycxdu―多输入－多输出系统状态空间表达式的一般形式为–单输入－单输出系统状态空间表达式的一般形式为588对于线性定常系统来说，状态空间模型的标准形式是DuCxyBuAxx系统A输入u输出y状态X结构关系图DBC5892.5.22.5.2由微分方程建立状态变量表达式由微分方程建立状态变量表达式步骤：–直接根据系统的物理机理建立相应的微分(连续系统）或差分（离散系统）方程组。–针对微分方程，定义一组状态变量，建立状态方程，并根据系统输出和状态之间的关系，建立系统的输出方程。状态变量的选取1.状态变量的选取是非唯一的。2.选取方法（1）可选取初始条件对应的变量或与其相关的变量作为系统的状态变量。（2）可选取独立储能（或储信息）元件的特征变量或与其相关的变量作为控制系统的状态变量。（如电感电流i、电容电压uc、质量m和速度v等。590线性微分方程中不含有输入函数导数项的系统的状态空间表达式–选取状态变量：–则有：1123,,,,nnxyxyxyxy12231111nnnnnnnxyxxyxxyxxyayaybu)()()()()(001)1(1)(tubtyatyatyatynnn591–系统状态空间表达式为：cxybuAxx)()()()(21txtxtxtxn1210100001000010naaaaA000bb001c592系统输入量中含有导数项–其一般形式为：)(')()()()(01)1(1)(01)1(1)(tububububtyatyatyatynnnnnnn–应选择以下n个变量作为一组状态变量–则状态变量如下niuhxxuhyxiii,,3,21101593其中0132211102112201110hahahabhhahabhhabhbhnnnnnnnnnnn令则有001122110hahahahabhnnnnnuhxaxaxaxaxnnnnnn1122110594–将上式改为矩阵向量形式为：–其中ducxybuAxx1210100001000010naaaaAnhhhb21001cd=h0＝bn595一般形式：当式中bn=0时，还可以按如下规则选择另一组状态变量。设)(')()()()(01)1(1)(01)1(1)(tububububtyatyatyatynnnnnnn1,,3,2,1,1niubyaxxyxiiiin596ducxybuAxx12101000010001000naaaaA110nbbbb100cd=05972.5.32.5.3由传递函数建立状态变量表达式由传递函数建立状态变量表达式1、设线性定常系统的传递函数为有理真分式(bn为零)2、传递函数以极点形式给出•系统传递函数只有单实极点（没有重极点）•系统传递函数含有重实极点情况598buAxxcxy1n210aaaa100001000010A100b1n10bbbc'''可控标准型599这种形式的状态空间表达式被称为可观测标准型buAxx12101000010001000naaaaA110'''nbbbb100ccxy可观测标准型600对角阵标准型(I)写成矩阵形式有对角阵标准型nnnnnxxxcccyuxxxxxx212121212111100601对角阵标准型(II)如果状态变量选择为)()(sUscsXiii那么系统输出则为niisXsY1)()(同样，经过反拉氏变换并展成矩阵形式有对角阵标准型nnnnnxxxyucccxxxxxx212121212111100602约当标准型称重极点对应的111001001为约当块nnnnnxxxxxcccccyuxxxxxxxxxx4321413121143214111432111100001016032.5.4、由状态空间表达式求传递函数阵DuCxyBuAxx若对上式求拉氏变换，并令初始条件为零，则有)()()(sBUsAXssX)()()(sDUsCXsY整理式得)()()(sBUsXAsI)()()(1sBUAsIsX根据传递函数阵的定义有DBAsICsUsYsG1)()()()(7.17.1状态空间的线性变换状态空间的线性变换回顾系统动态方程建立的过程，无论是从实际物理系统出发，还是从系统方块图出发，还是从系统微分方程或传递函数出发，在状态变量的选取方面都带有很大的人为的随意性，因而求得的系统的状态方程也有很大的人为因素，很大的随意性，因此会得出不同的系统状态方程。所以说系统动态方程是非唯一的。虽然同一实际物理系统，或者同一方块图，或同一传递函数所产生的动态方程各种各样，但其独立的状态变量的个数是相同的，而且各种不同动态方程间也是有一定联系的，这种联系就是变量间的线性变换关系。605如果我们将各变量次序颠倒，即令：将代入该动态方程：(1)606因此有:上式与（1）相同。也就是说（1）与（2）代表的动态方程是一种线性变换的关系。进一步，由于上述非奇异的变换矩阵T可以有无数种，所以系统的动态方程也有无数种。(2)6077.1.1线性变换①思路：（规范型）（不规范）等价变换yuDxCyuBxAxDuCxyBuAxxxpx虽然通过非奇异的线性变换，可以求出无数种系统的动态方程，但是有几种标准型对我们特别有用，如可控标准型、可观标准型、对角标准型和约当标准型。②变换前后系数矩阵关系：,,xPxxPxDuxCPyBuxAPxP代入原状态方程，有DuxCPyBuPxAPPx11P为nxn的常数非奇异矩阵。DDCPCBPBAPPA11,,,性变换为等价变换。实现他们之间转换的线价动态方程，相应的动态方程称为等互为相似系统和称满足条件的系统,},,,{D}C,B,{A,DCBA7.1.2线性变换的不变性线性定常系统的特征方程，特征根与特征向量的特征向量。为矩阵的关于特征值则称如果，存在向量，若矩阵的特征值特征向量：特征根。特征方程的根，也称为的特征值矩阵的特征方程线性系统3:2.1.AA0AIAIfDCBA.)det()(},,,{线性变换的不变性1。传递函数阵的不变性2。特征方程和特征值的不变性)()()()(sGBAsICDBAsICDsG11610•系统特征值的不变性及系统的不变量–特征值的不变性和系统的不变量对上面的系统进行变换xPx（即xPx1），得：DuxCPyBuPxAPPx11其特征方程为：AIAIPPPAIPAPPPPAPPPPAPPI1111111611特征方程写成多项式00111aaaAInnn经过非奇异变换后，系统的特征值不变，系统的特征方程系数也不变。特征方程多项式的系数称为系统的不变量。612对线性系统进行非奇异变换的目的:便于系统分析与综合设计。1.系统矩阵Ａ对角化、约当化2.{A,c}化为可观测标准型3.化可控系统为可控标准型uaaaun100100001000010110xbAxx任何一个可控系统，当A，b不具有可控标准型时，一定可通过适当的变换化为可控标准型。613可控性矩阵]bbb[1ncAAQ一个不具有可控标准型的可控系统，可以通过线性变换化为可控标准型。ubAxx设xPxuPxPPxbA11100b,10000100001011101PaaaAPPn614变换阵P可由以下计算获得：nPppp21设变换阵Ｐ(1)计算(２)计算]bbb[1ncAAQ111]bbb[ncAAQnnnnnncSSSSSSSSSQ2122221112111615(３)取出的最后一行，构成p1行向量选择][211nnnnSSSp(４)构造11111pppnAAP1P1cQ(5)计算P。7.27.2线性定常系统状态方程的解线性定常系统状态方程的解7.2.1齐次状态方程的解)(自由运动Axx(1)(1)幂级数法幂级数法设解为：0kkkkk2210tbtbtbbbttx)()()(tbbbtbtbbbkk101k1kk1kk21tAAxxkkt2txbAb02221bAbkkk0!1bAb01617)()!()!(!)()(0xk1bk121AtIk1A21tAtx0kkk0x0kk22k0k20200tAbtAtAtbAtbbb0)0()(xtxeAt即],,!1[0状态转移矩阵称为矩阵指数定义kkkAttAek⑵拉氏变换法由两边取拉氏变换，得sX(s)-x(0)=AX(s)(sI﹣A)X(s)=x(0)X(s)=(sI﹣A)-1.x(0)两边取拉氏反变换x(t)=L-1[X(s)]=L-1[(sI-A)-1x(0)]=L-1[(sI-A)-1]x(0)比较前式，有eAt=L-1[(sI-A)-1]Axx)()()()(0,)()()()()(000ttA0Attxtttxetxt0xt0xetx0初始时刻当6197.2.2状态转移矩阵的性质.))(BtAttBAAsAtstAeeeBAABBAeeest＋（时，有，当和对于方阵为标量时，和当ф(t)=eAt=I+At+(1/2)A2t2+…+(1/k！)Aktk+…⑴ф(0)=I─初始状态AAttA)0(,)()((t)(2)⑶ф-1(t)=ф(-t)，ф-1(-t)=ф(t)-----可逆性ф-1(t-t0)=ф(t0-t)⑷ф(t1±t2)=ф(t1)ф(±t2)=ф(±t2)ф(t1)-----线性关系[Φ(t)]k=Φ(kt)⑸x(t2)=ф(t2-t1)x(t1)620则x(t2)=ф(t2)x(0)=ф(t2)[ф-1(t1)x(t1)]=ф(t2)ф(-t1)x(t1)=ф(t2-t1)x(t1)（6）ф(t2-t0)=ф(t2-t1)ф(t1-t0)=e(t2-t1)Ae(t1-t0)A——可分阶段转移∵x(t1)=ф(t1)x(0)(7)e(A+B)t==eAt.eBt=eBt.eAt(AB=BA)e(A+B)t≠eAt.eBt≠eBt.eAt(AB≠BA)(8)引入非奇异变换P，(9)两种常见的状态转移矩阵PePetAt1APtP1)(621ttnneetA00)(,0011ttttmttmmeteeemtteetA000)!1()(,0010011若A阵为m阶的约当阵，若A为n阶对角矩阵,622例7-1试求如下线性定常系统的状态转移矩阵Ф(t)和状态转移矩阵的逆。【解】对于该系统，其状态转移矩阵由下式确定由于其逆矩阵为21213210xxxx1()t3210A])[()(11AsILetAt321321000ssssAsI)2)(1()2)(1(2)2)(1(1)2)(1(3213)2)(1(1)(1ssssssssssssssAsI因此=])[()(11AsILetAttttttttteeeeeeee22222222由于,故可求得状态转移矩阵的逆为1()()ttttttttttAteeeeeeeeet222212222)(6237.2.3矩阵转移函数的计算Ate方法一直接计算法(矩阵指数函数)可以证明，对所有常数矩阵A和有限的t值来说，这个无穷级数都是收敛的。方法二线性变换法（对角线标准形与Jordan标准形法）若可将矩阵A变换为对角线标准形，那么可由下式给出kkkAttAktAtAAtIe03322!1!3!2Ate110021PeeePPPeettttAtn式中，P是将A对角线化的非奇异线性变换矩阵。类似地，若矩阵A可变换为Jordan标准形，则可由下式确定出1AtJteSeSAte624方法三拉氏变换法为了求出，关键是必须首先求出（sI-A）的逆。一般来说，当系统矩阵A的阶次较高时，可采用递推算法。])[(11AsILeAtAte例7-2考虑如下矩阵,试用线性变换法和拉氏变换两种方法计算。A【解】线性变换法由于A的特征值为0和-2（），故可求得所需的变换矩阵P为P=因此，由2010Ate120,22011110021PeeePPPeettttAtn625拉氏变换法由于可得因此201201000ssssAsI210)2(11)(1ssssAsItteeAsIL2211At0)1(211])[(etttoAteeeee2220)1(211210211002011可得：626例7-3设有一控制系统，其状态方程为Axx320100010A在t0=0时，状态变量的初值为[x1(0)x2(0)x3(0)],试求该方程的解。3201001)(:sssAsI解)2)(1(20)3(013)1)(2()()(21sssssssssssAsIAsIadjAsI627)2)(1/()2)(1/(20)2)(1/(1)2)(1/()3(0)2)(1(/1)2)(1(/)3(/1ssssssssssssssssss22112212021112112025.0115.025.0125.1/1sssssssssssssss628ttttttttttttAteeeeeeeeeeeeAsILet222222112220205.05.05.025.11])[()()0()2()0()22()0()()0()2()0()5.05.0()0()5.025.1()0()0()0()0()()0()()()()()(3222322232221321321xeexeexeexeexeexeexxxxtxttxtxtxtxtttttttttttt6297.2.4.非齐次状态方程的解BuAxx⑴直接法（积分法）BueAXxexexAexedtdAtAtAtAtAt)()(dBuextxedxeddtAAttA)()0()()(00dButxtdBuexetxtttAAt00)()()()0()()0()((2)拉氏变换法sX(s)-x(0)=AX(s)+Bu(s)(sI-A)X(s)=x(0)+Bu(s)X(s)=(sI-A)-1x(0)+(sI-A)-1Bu(s)则x(t)=￡-1[(sI-A)-1x(0)]+￡-1[(sI-A)-1Bu(s)](由eAt=￡-1[(sI-A)-1]可得)dButxtdBuexetxtttAAt00)()()()0()()()0()(630例7-4求下列系统的时间响应，其中，u(t)为t=0时作用于系统的单位阶跃函数，即u(t)=1(t)。【解】对该系统状态转移矩阵为因此，系统对单位阶跃输入的响应为：即uxxxx1032102121103210BAttttttttAteeeeeeeeet22222222)(dteeeeeeeexetxtottttttttAt)(1102222)0()()(2)()(2)()(2)()(2)(tttttttttttteeeexxeeeeeeeetxtx22212222212121)0()0(2222)()(tttteeeetxtx22212121)()(如果初始状态为零，即x(0)=0,可将x(t)简化为6317.37.3线性定常系统的可控性与可观测性分析线性定常系统的可控性与可观测性分析线性连续系统的可控性与可观性的概念线性连续系统的可控可观判据对偶原理设线性定常连续系统的状态空间表达式为：)()()()()()(tDutCxtytButAxtx7.3.1概念632如果存在一个控制u(t)，能在有限时间间隔[to,t1]内，使系统从其一初态x(to)转移到任意指定的终态x(t1)，则称此状态x(to)在时刻to是可控的。若x(to)对所有的时刻都是可控的，则称x(to)为一致可控。若系统的每一个状态都可控，称系统为状态完全可（能）控，简称状态可控（只要有一个状态变量不可控，则系统不可控）。1.可控性定义如果能找到一个无约束的控制向量,在有限的时间间隔内，使任一给定的初始输出转移到任一最终输出,那么称由上式所描述的系统为输出可控的。()ut01ttt0()yt1()yt633系统在零输入u(t)＝0作用下，对任意初始时刻to，若能在有限时间间隔[to,tf]之内，根据从to到tf对系统输出y(t)的观测值，唯一地确定系统在to时刻的状态x(to)，则称状态系统x(to)是to时刻可观测的。若状态在所有时刻都是可观测的，称该状态为一致可观测的。若状态空间中每一个状态都是可观测的，称该系统是状态完全可观测的，简称系统可（能）观测。（只要有一个状态变量不能（可）观测，则系统不可观测）。2.可观测性定义可控标准型：1000B,aaaa1000001000010A1n2107.3.2.可控性判据线性定常连续系统状态完全可控的充要条件是可控性判别阵：必须满秩。即（n为系统维数）][12BABAABBQnCnrankQc判据一：如果系统的状态方程为BuAxxrnnnrnRBRARtuRtx,,)(,)(6351110ABBQc试判别其状态的可控性。u101101xxxx2121解：例7-5设系统状态方程为：nrankQc2系统可控！例7-6已知三阶二输入系统状态方程,试判别其状态的可控性。21321321100110110010011uuxxxxxx1211100101011211102cQ不可控！636设线性定常系统具有互异的特征值，则系统可控的充要条件是，系统经非奇异变换后的对角线标准型方程：uxxn0021中，阵不包含元素全为零的行。判据二:uxxxxxx752100050007)1321321uxxxxxx750100050007)232132121321321570410100050007)3uuxxxxxx21321321570400100050007)4uuxxxxxx例7-7试确定如下几个经非奇异变换后的对角线标准型系统的可控性。√×√×uxJJJxk21例7-8试判断下列已经非奇异变换成约当标准型的系统的可控性。u340xxx200040014xxx1321321)21321321030024200040014)2uuxxxxxx中，与每个约当小块的最后一行相对应的阵中的所有那些行，其元素不全为零。（若两个约当块有相同特征值，此结论不成立。）),,2,1(kiJi约当标准型判据三：√×判据一:线性定常连续系统状态完全能观测的充分必要条件为可观测性矩阵:10nCACACQ2.可观测性判据必须满秩，即rankQo=n（n为系统维数）可观测标准型：100,1000100010001210CaaaaAn)(CBTcQ640例7-9已知系统的A,C阵如下，试判断其可观性。uxxxx113112212121210101xxyy121201010CACQ例7-10试判别如下系统的可观测性。解：015411C55110CACQ55015411CA解：√×641xcyxxn0021的矩阵中不包含元素全为零的列。设线性定常连续系统具有不相等的特征值,则其状态可观测的充要条件是系统经非奇异变换后的对角线标准型:c例7-11试判别以下系统的状态可观测性.321321100050007xxxxxx32121130023xxxyy判据二:√642kJJJx0021中,与每个约当块首行相对应的矩阵中的那些列,其元素不全为零。(如果两个约当块有相同的特征值,此结论不成立)。),,3,2,1(kiJi约当标准型c判据三:643例7-12试判别下列系统的状态可观测性。432143213001320012)1xxxxxxxx43212110100011xxxxyyuxxxxxx101200120001)2321321321011xxxy√×644对偶原理下面介绍由R.E.Kalman提出的对偶原理，该原理揭示了可控性和可观测性之间的关系。考虑由下述状态空间表达式描述的系统S1：CxyBuAxxnmrnnnmrnRCRBRARyRuRx,,,,,以及由下述状态空间表达式定义的对偶系统S2：zBnvCzAzTTTnrTmnTnnTrmnRBRCRARnRvRz,,,,,对偶原理当且仅当系统S1状态可观测（状态可控）时，系统S2才是状态可控（状态可观测）的。645证明对于系统S1：状态可控的充要条件是n×nr维可控性矩阵的秩为n。状态可观测的充要条件是n×nm维可观测性矩阵的秩为n。对于系统S2：状态可控的充要条件是n×nm维可控性矩阵的秩为n。状态可观测的充要条件是n×nr维可观测性矩阵的秩为n。对比这些条件，可以很明显地看出对偶原理的正确性。利用此原理，一个给定系统的可观测性可用其对偶系统的状态可控性来检检和判断。简单地说，对偶性有如下关系：][1BAABBn])([1TnTTTTCACAC])([1TnTTTTCACAC][1BAABBnTTTBCCBAA,,6467.47.4线性定常系统的状态反馈和状态观测器线性定常系统的状态反馈和状态观测器状态,输出反馈与极点配置问题的提法可配置条件(极点配置定理)极点配置的算法6477.4.1状态,输出反馈与极点配置状态反馈给定单输入单输出线性定常被控系统ABuxx11,,)(,)(nnnnRBRARtuRtx选取线性反馈控制律为式中K∈R1×n为状态反馈增益矩阵或线性状态反馈矩阵。下图分别给出了开环控制系统和具有状态反馈的系统的结构图。uBRIsCyAk-+++xx(a)开环控制系统(b)闭环反馈控制系统Kxru648代入系统，得到ABuxx由此可见，系统的响应特性将由闭环系统矩阵A-BK的特征值决定。如果矩阵K选取适当，则可使矩阵A-BK构成一个渐近稳定矩阵。矩阵A-BK的特征值即为闭环系统的极点。这种使闭环系统的极点任意配置到所期望位置的问题，称为极点配置问题。Kxru)()()()(tBrtxBKAtx649uxyB∫CAx输出反馈至状态微分H-BrxBHCABHCxBrAxxCxyBHyBrAxx)(输出反馈Hyru:反馈r650可配置条件_极点配置定理考虑线性定常系统假设控制输入u的幅值是无约束的。如果选取控制规律为ABuxx式中K为线性状态反馈矩阵。定理(极点配置定理)线性定常系统可通过线性状态反馈任意地配置其全部极点的充要条件是，此被控系统状态完全可控。该定理对多变量系统也成立。证明(对单输入单输出系统)1、充分性2、必要性Kxru651极点配置定理_充分性1.充分性。如果线性系统状态完全可控，一定存在非奇异变换，使其变换为可控标准形。定义非奇异线性变换矩阵P为P=QW，其中Q为可控性矩阵，ABuxx1[]nQBABAB1212311101001000nnnnaaaaaWa式中ai为特征多项式的系数：nnnnasasasAsI111652定义一个新的状态向量xPx如果可控性矩阵Q的秩为n（即系统是状态完全可控的），则矩阵Q的逆存在，并且可将原线性系统改写为ccABuxx111210100000100000101ccnnnAPAPBPBaaaaABuxx上式为可控标准形。选取一组期望的特征值为，则期望的特征方程为12,,,nuuu0)())((11121nnnnnasasassss653设11[]nnKKP由于，此时该系统的状态方程为相应的特征方程为0ccsIABK因为非奇异线性变换不改变系统的特征值，当利用u=r-Kx作为控制输入时，相应的特征方程与上式相同，均有如下结果。1111111111000()()()0ccnnnnnnnnnnsssIABKaasasasasa这是具有线性状态反馈的闭环系统的特征方程，它一定与期望特征方程相等。通过使s的同次幂系数相等，可得xKrxKPrKxrurBxKBAxccc)(654nnnaaaaaa222111求解上述方程组，得到的值，则i11111112211[][]nnnnnnKKPPaaaaaaaaP如果系统是状态完全可控的，则通过对应于上式所选取的矩阵K，可任意配置所有的特征值。充分性得证。655极点配置定理_必要性即已知闭环系统可任意配置极点，证明被控系统状态完全可控。现利用反证法证明。先证明如下命题：如果系统不是状态完全可控的，则矩阵A-BK的特征值不可能由线性状态反馈来控制。假设原线性系统状态不可控，则其可控性矩阵的秩小于n，即ABuxxnqBAABBrankn][1则必有状态变量与控制u无关，因此，不可能实现全状态反馈，则不可控子系统的特征值就不能任意配置。所以，为了任意配置矩阵A-BK的特征值，此时系统必须是状态完全可控的。必要性得证。656极点配置的算法给定线性定常系统，若线性反馈控制律为，则可由下列步骤确定线性反馈矩阵K，使A-BK的特征值为μ1,μ2,…μn，即闭环系统的期望极点值(如果μi是复数特征值，则其共轭必定也是A-BK的特征值)。◆考察系统的可控性条件。如果系统是状态完全可控的，则可按下列步骤继续。◆计算系统矩阵A的特征多项式，确定的值。BuAxxnaaa,,,21Kxru657◆确定将系统状态方程变换为可控标准形的变换矩阵P。若给定的状态方程已是可控标准形，则P=I。此时无需再写出系统的可控标准形状态方程。非奇异线性变换矩阵P=QW。◆利用给定的期望闭环极点，可写出期望的特征多项式为nnnnnasasassss11121)))（（（从而确定出a1,a2,…an的值。◆最后得到状态反馈增益矩阵K为1112211][PaaaaaaaaKnnnn658【例】考虑如下线性定常系统BuAxx100,651100010BA利用状态反馈控制，希望该系统的闭环极点为s=-2±j4和s=-10。试确定状态反馈增益矩阵K。【解】该系统已是可控标准形。首先需检验该系统的可控性矩阵。由于可控性矩阵为3161610100][2BAABBQ得出detQ=-1。因此，rankQ=3。因而该系统是状态完全可控的，可任意配置极点。下面用两种方法求解。659方法1：利用刚才介绍的求解步骤，计算系统矩阵A的特征多项式，求特征值。015665110013221323asasasssssssAsI1,5,6321aaa则期望的特征方程为02006014)10)(42)(42(3221323asasasssssjsjs200,60,14321aaa则由可得[2001605146][199558]K1112211][PaaaaaaaaKnnnn660方法2：设期望的状态反馈增益矩阵为并使[sI-A+BK]和期望的特征多项式相等，可得][321kkkK][100651100010000000321kkksssBKAsI20060141)5()6(65110012312233321ssskskskskskkss令对应系数相等得即8,55,199321kkk]855199[K