自动控制原理课件-全,自动控制原理课件ppt

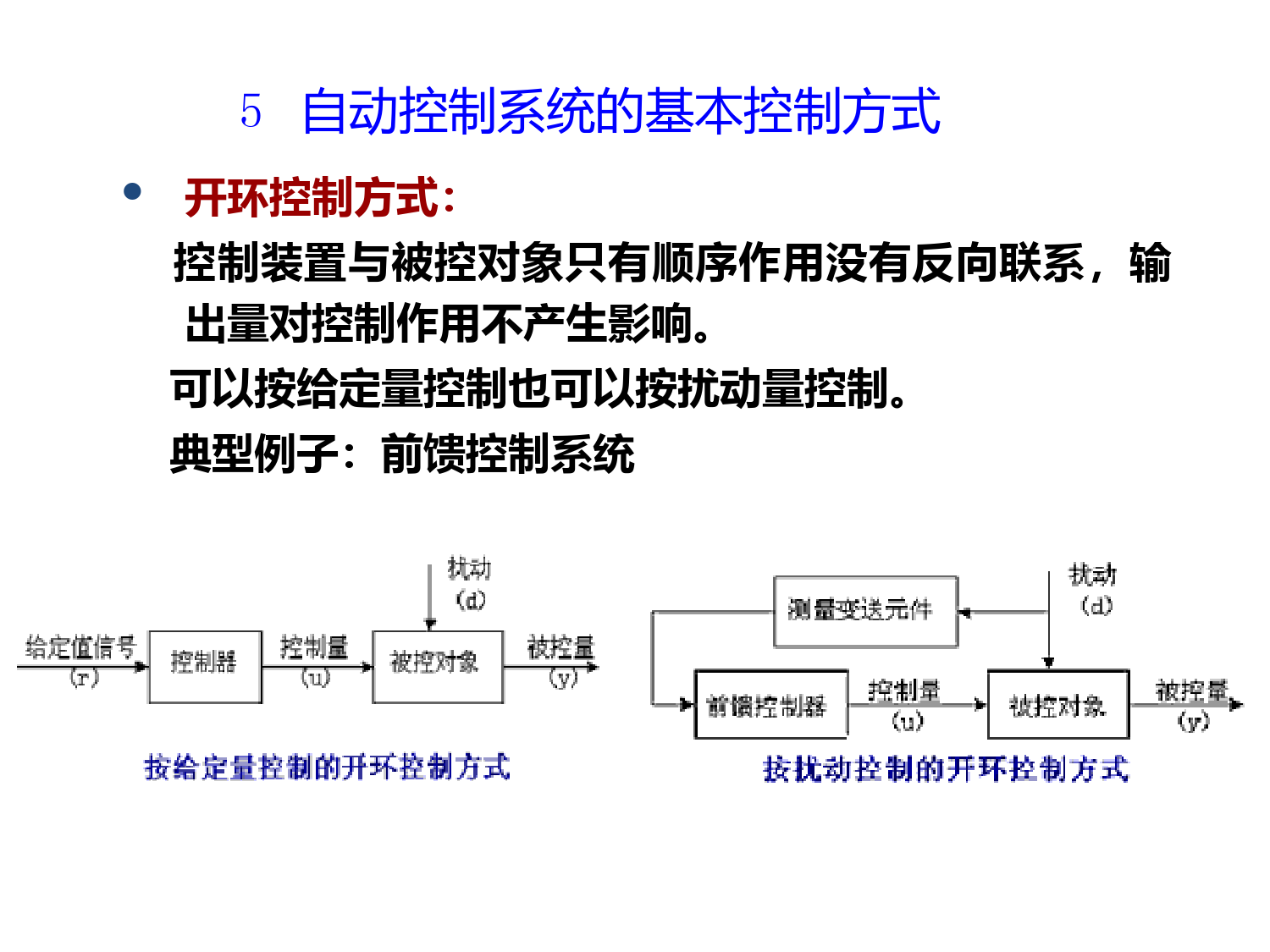
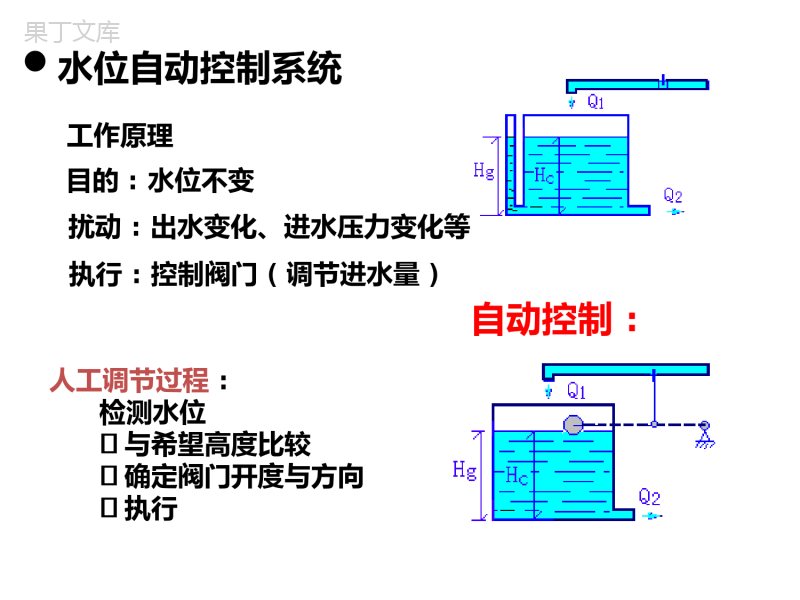
自动控制原理A主讲：王桂荣教材：自动控制原理─简明教程（第二版）胡寿松主编基本内容第一章控制系统导论第二章控制系统的数学模型第三章线性系统的时域分析法第四章线性系统的根轨迹法第五章线性系统的频域分析法第六章线性系统的校正方法第七章非线性系统分析第八章采样控制系统第一章控制系统导论第一节自动控制的基本原理1自动控制技术及应用•什么是自动控制？是指在没有人直接参与的情况下利用外加的设备或装置使机器设备或生产过程的某个工作状态或参数自动的按照预定的规律运行。•什么是自动控制技术？在现实生活中的各个领域应用自动控制这种方法进行工业生产或其它用途，使之成为一种技术。•应用：从工业生产到经济、生物、医学、到航空、导弹、机器人、核动力等高科技领域。水位自动控制系统工作原理目的:水位不变扰动:出水变化、进水压力变化等人工调节过程:检测水位与希望高度比较确定阀门开度与方向执行执行:控制阀门(调节进水量)自动控制:2自动控制理论•什么是自动控制理论？研究自动控制共同规律的技术科学。发展初期以反馈理论为基础，主要应用于工业控制。自动控制理论根据研究对象分为：经典控制理论40-50年代形成，适用于SISO（单输入－单输出）系统目标：反馈控制系统的稳定基本方法：传递函数，频率法，PID调节器现代控制理论：60-70年代形成，适用于MIMO（多输入－多输出）系统目标：最优控制自动控制理论的内容自动控制理论经典控制理论(19世纪中叶--20世纪50年代)线性非线性根轨迹法频域法时域法波波夫法李雅普诺夫法描述函数法相平面法采样控制Z变换法现代控制理论(60年代以来)状态反馈控制最优控制智能控制预测控制自适应控制模糊控制大系统多层分散控制•什么是反馈？把输出量送回到输入端，并与输入信号相比较产生偏差信号的过程。•人取书的反馈控制系统负反馈：反馈信号与输入信号相减，使偏差越来越小。正反馈：反馈信号与输入信号相加。我们通常所说的反馈控制采用负反馈。3反馈控制原理眼睛大脑手臂、手眼睛输入信号书位置输出量手位置注意闭环控制4反馈控制系统的基本组成一个完整的控制系统包括被控对象和控制装置两大部分，控制装置由具有一定职能的各种基本元件组成。•测量元件：检测被控制的物理量•给定元件：给出与期望的被控量相对应的系统输入量•比较元件：把被控量的实际值与参据量相比较，得到偏差信号•放大元件：将偏差信号进行放大，用以推动执行元件。•执行元件：直接推动被控对象，改变其输出量•校正元件：为改善系统性能增加的补偿元件5自动控制系统的基本控制方式•反馈控制方式：按偏差进行控制，减小或消除偏差抑制任何内外扰动对被控量的影响控制精度高，元件多、结构复杂等5自动控制系统的基本控制方式开环控制方式：控制装置与被控对象只有顺序作用没有反向联系，输出量对控制作用不产生影响。可以按给定量控制也可以按扰动量控制。典型例子：前馈控制系统5自动控制系统的基本控制方式复合控制方式：按偏差控制与按扰动控制结合起来，构成前馈-反馈控制系统。实例原理：只要浮子不在给定位置上,电机就要工作,也就是说,系统最终不会存在误差。前述水位自动控制系统中,如果用水量增加(减少),则浮子一定要偏离给定位置,必须开大(关小)阀门。第二节自动控制系统示例系统功能框图描述控制过程：假设Hc↓→浮子↓（测量出Hc，和给定的位置Hg作比较）→阀门↑→Q1↑→Hc↑第三节自动控制系统的分类•按控制方式分：反馈控制、开环控制、复合控制•按系统功能分：温度控制、压力控制、位置控制、液位控制等，即被控量类型•按元件类型分：机械、电动、气动、液压、生物等•按系统性能分：线性与非线性、连续与离散、定常与时变确定与不确定等。•按参据量变化规律分：恒值、随动、程序1线性连续控制系统控制作用的信号是连续的，控制器通常为模拟电子器件线性微分方程：)()()()()()((t)dtda(t)dtda1111011n1n1nn0trbtrdtdbtrdtdbtrdtdbtcatcdtdaccmmmmmmnnC(t):被控量；r(t)：系统输入量；a0-an,b0-bn是系数。线性定常连续控制系统按输入量的变化规律不同分：•恒值控制系统：输入量是一个常值要求被控量等于常值主要研究扰动对被控对象的影响。如温度控制等•随动控制系统：输入量的大小不可预知（可能有规律或无规律）要求被控量随之变化。又称跟踪系统。如函数记录仪、电子配钥匙•程序控制系统：输入量按预定规律随时间变化g=f(t)要求被控量迅速准确的复现。如数控机床，部分供水系统2线性定常离散控制系统控制作用的信号是断续的或数字量（即在时间上是离散的），采用计算机构成的系统通常都是离散控制系统。差分方程：)()1()1()()()1()1(a)(a110110krbkrdtdbmkrbmkrbkcakcankcnkcmmnn离散信号连续信号采样3非线性控制系统只要有一个元件的输入输出特性是非线性的。第四节自动控制系统的基本要求1基本要求的提法稳、快、准稳定性：保证系统正常工作的先决条件。•什么是稳定的控制系统？被控量偏离期望值的初始偏差随时间的增长逐渐减小并趋于零。线性系统的稳定性由系统结构所决定。•过渡过程系统收到扰动或有输入量时，控制过程不会立即完成，而是有一定的延缓，使被控量恢复期望值或跟踪参据量有一个时间过程。快速性：要求过渡过程的形式和快慢，即动态性能。过渡过程的时间（调节时间）最大振荡幅度（超调量）准确性：过渡过程结束后，被控量达到的稳态值应与期望值一致。稳态误差（衡量控制精度的重要标志）2典型外作用（1）阶跃函数模拟设定值的突然变化，如电源电压突然跳动等。表示t=0时，出现幅值为R的阶跃变化并一直保持下去。R=1时，为单位阶跃函数1(t),即f(t)=R·1(t)一般将阶跃函数作用下系统的响应特性作为评价系统动态性能指标的重要依据。0,0,0tRt)(tfR(2)斜坡函数：速度函数模拟设定值的连续变化。表示在t=0时刻开始，以恒定的速度R随时间变化。R=1时，为单位斜坡函数t，即f(t)=R·t。)(tf0,0,0tRtt)(tf0,0,0221tRtt(3)加速度函数：抛物线函数R=1时，为单位加速度函数t2/2。（4）脉冲函数模拟外界的干扰信号，用于分析系统偏离稳态又恢复到稳态的运动过程。两个阶跃函数合成的脉动函数，t0越小矩形的宽度越小高度越大；t0趋于零时，即脉动函数的极限为脉冲函数，宽度为0，高度无穷大。)](1)(1[lim0000ttttAt)(tfδ(t)A/t0A/t0A/t0t0t0单位脉冲函数：是一个持续时间无限短、脉冲幅度无限大、信号对时间的积分为1的矩形脉冲。01dt)t(0)t(t,0t,0t0,1lim0（5）正弦函数随动控制系统。)sin(tA)(tf正弦函数作用下的频率响应是研究性能的重要依据。第二章控制系统的数学模型1什么是数学模型？描述系统内部物理量之间关系的数学表达式。2数学模型有多种形式：•时域数学模型：微分方程（连续系统）差分方程（离散系统）状态方程•复域数学模型：传递函数、结构图•频域数学模型：频率特性建立控制系统的数学模型是分析和设计控制系统的首要工作。1.拉氏变换的定义：例：f(t)=1(t))]([)(1sFLtfs110s1es1dtssedte)t(10st00stst（1）t<0时，f(t)=0（2）t≥0时，f(t)分段连续)]t(f[L)s(F记为：0stdte)t(f)s(F则：0stdte)t(f（3）第一节拉普拉斯变换s110s1es1dtssedte)t(10st00ststs110s1es1dtssedte)t(10st00stst（1）线性定理：（齐次性，叠加性）)s(aF)]t(af[L)s(F)s(F)]t(f)t(f[L2121)0(f)s(sFdt)t(dfL)s(Fs)]t(f[Lnn（2）微分定理：当初始值为0时，＝sF(s)对原函数进行一次微分相当于象函数用s乘一次。2.常用拉氏变换定理当初始值为0时，ssFsdttfdttfLt)()(])([0s)s(Fnns)s(F])dt)(t(f[L（3）积分定理：对原函数进行一次积分相当于象函数用s除一次。)(lim)(lim0ssFtfst)(lim)(lim0ssFtfst（4）初值定理：（5）终值定理：)()]([asFtfeLat（6）位移定理：初值定理与终值定理举例：例：ate)t(fas1)s(F1ass)s(sFlims1elimat0t0elimatt0ass)s(sFlim0s)s(sFlim)t(flims0t)s(sFlim)t(flim0st结论：根据初值定理和终值定理可直接根据S域的特性分析系统在时域中输入作用瞬时的特性以及稳态情况。终值定理：则：初值定理：3拉普拉斯反变换(由象函数F(s)求原函数f(t))部分分式展开法)()()()(1111110nmasasasbsbsbsbsAsBsFnnnnmmmm分母因式分解，得：)())(()()()(211110nmmmmssssssbsbsbsbsAsBsFs1,s2,…sn是A(s)=0的根，称为F(s)的极点。)())(()()()(211110nmmmmssssssbsbsbsbsAsBsF情况一：F(s)有不同极点,这时,F(s)总能展开成如下简单的部分分式之和。)()(limF(s),,0)(),,2,1(sFsscscsAnisissiiiii处的留数。在极点称为是常数的根是式中nnsscsscsscsF2211)(()()tsntstsnecececsFLtf21211)]([)(()例题1：求的原函数f(t)。342)(2ssssF解：将分母因式分解并按部分分式展开：31)3)(1(2)(21scscssssF2132lim)()1(lim111sssFscss2112lim)()3(lim332sssFscss因此，原函数tteetf32121)(tttssseeetfsssscsssscssssc3233221110115161)(101])3)(2)(1(1)3[(lim151])3)(2)(1(1)2[(lim61])3)(2)(1(1)1[(lim321)3)(2)(1(1)(:321scscscssssF练习321)3)(2)(1(1)(:321scscscssssF练习jscjscjsjsssF11)1)(1(3)(21解：分别按照表2-3的17项和15项得：tjtjececf)1(2)1(1例题2：求的原函数f(t)。223)(2ssssF1)1(41)1(11)1(3)(222ssssssF1)1(141)1(11)1(3)(222ssssssF)sin4(costteftnnrrrrrrnrrsscsscsscsscsscsssssssBsAsBsF1111111111)()()()()()()()()(仍按以前的方法计算系数,,,1nrcc假若F(s)有r重极点,而其余极点均不相同。那么情况二：F(s)有重极点。)]()[(lim)()(lim11111sFssdsdcsFsscrssrrssr式中1)1(lim])1()1(1[lim1)1(1)1(lim1)1()1()1(1)(1331233134122333sdsdsssdsdcssscscscscscsssFsss例题：121)(111)1(1)1(1)(1)1(1lim1)2(lim!21223304311tttsseteettfsssssFssscsc作业：求f(t)。545)(.2)2)(1()3(6)(.12ssssFsssssF2-2控制系统的时域数学模型1线性元件的微分方程例1.图示无源网络，列写以ui(t)为输入量，uo(t)为输出量的网络微分方程。RCui(t)uo(t)Li(t))()()(1)(tutRidttiCdttdiLidttiCtuo)(1)()()()()(22tutudttduRCdttudLCiooo根据基尔霍夫定律列写回路方程：消去中间变量i(t)得到输入输出关系的微分方程：dttduCtio)()(例2.列写图示电枢控制直流电动机的微分方程。电枢电压ua(t)为输入量，电动机转速ωm(t)为输出量，Ra、La为电枢电路的电阻和电感，Mc为折合到电动机轴上的总负载转矩。aaaaaaEtiRdttdiLtu)()()(工作实质：电能转化为机械能RaEauaωm-SMLaia++-负载Jm，fm直流电动机的运动方程由三部分组成：①电枢电路的电压平衡方程：②电磁转矩方程：③电动机轴上的转矩平衡方程：电枢旋转时产生的反电势大小与激磁磁通及转速成正比，方向与ua(t)相反。Ea=Ceωm(t))()(tiCtMammCm：电动机转矩系数)()()()(tMtMtfdttdJcmmmmmJm、fm：电动机和负载折合到电动机轴上的转动惯量和黏性摩擦系数。上述三方程联立消去中间变量ia(t)、Ea、Mm(t)，得到以ωm(t)为输出量，ua(t)为输入量的直流电动机微分方程：在工程应用中La较小，通常忽略不计，如果Ra和Jm也很小可忽略时，此微分方程可简化为：总结：列写元件微分方程的步骤：确定输入、输出量→列写微分方程→消去中间变量)()()()()()()()(22tMRdttdMLtuCtCCfRdttdJRfLdttdJLcacaammemmammamamma)()(tutCame微分方程的标准写法：输出项在左边，输入项在右边，导数项降幂排列。2控制系统微分方程的建立步骤：①画出系统方框图②列写各元件的微分方程③消去中间变量注意：①信号传递的单向性。②前后连接的两个元件中，后级对前级的负载效应。负载效应问题系统的各部分串联连接时，后面部分通常是前面的负载，分成两个独立环节时应考虑其影响。举例：速度控制系统的微分方程控制系统的主要部件（元件）：给定电位器、运放K1、运放K2、功率放大器、直流电动机、减速器、测速发电机3线性系统的基本特性线性系统的重要性质就是可以应用叠加原理：叠加性和齐次性。)()()()(22tftcdttdcdttcd设线性微分方程：叠加性：若)()(,)()()()(,)()(2211tctctftftctctftf时时则：)()()(,)()()(2121tctctctftftf时齐次性：)()(,)()(11tActctAftf时应用：两个外作用同时加于系统所产生的总输出等于各个外作用单独作用时分别产生的输出之和，且外作用数值增大若干倍时输出亦相应增大同样的倍数。4线性定常微分方程的求解目的：用数学的方法定量研究给定输入量和初始条件的系统输出量随时间变化的特性。方法：经典法和拉氏变换法例：已知L=1H，C=1F，R=1Ω，且电容上初始电压uo(0)=0.1v,初始电流i(0)=0.1A,电源电压ui(t)=1v,求电路突然接通电源时，电容电压uo(t)的变化规律。RCui(t)uo(t)Li(t)解：已知网络微分方程)()()()(22tutudttduRCdttudLCiooo12.01.01)()(22ssssssUsUio方程两边分别取拉氏变换，得初始条件非零因电路突然接通电源，故ui(t)为阶跃输入，Ui(s)=1/s.方程两边求拉氏反变换]12.01.01)([)]([)(2211ssssssULsULtuioo)30866.0sin(2.0)120866.0sin(15.115.05.0otottete输入电压产生的输出分量，与初始条件无关，称为零初始条件响应。初始条件产生的输出分量，与输入电压无关，称为零输入响应。统称为网络的单位阶跃响应。利用拉氏变换的初值定理和终值定理可根据Uo(s)直接求出uo(t)的初始值和终值。VssUtuusotoo1.0)(lim)(lim)0(0VssUtuusotoo1)(lim)(lim)(0总结：拉氏变换法求解线性定常微分方程的过程：（1）考虑初始条件，对微分方程的每一项分别进行拉氏变换，转为复变量s的代数方程；（2）由代数方程求出输出量拉氏变换函数的表达式；（3）对输出量求拉氏反变换，得出输出量的时域表达式。2-3控制系统的复域数学模型1传递函数的定义和性质1）定义：零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。线性定常系统的n阶微分方程一般可表示为：)()()()()()((t)dtda(t)dtda1111011n1n1nn0trbtrdtdbtrdtdbtrdtdbtcatcdtdaccmmmmmmnn)()()()()()()()(011101110sRbssRbsRsbsRsbsCassCasCsasCsammmnnnn在零初始条件下，对微分方程进行拉氏变换，得)s(Rb)s(sRb)s(Rsb)s(Rsb)s(Ya)s(sYa)s(Ysa)s(Ysa011m1mmm011n1nnn)()()()()()()()(01110111sRbssRbsRsbsRsbsYassCasYsasYsammmmnnnnn)()()()()()()()(0111111sRbssRbsRsbsRsbsCassYasYsasYsammmmnnnnn)()()()()()()()(011100111sRbssRbsRsbsRsbsYassYasYsasYsammmnnnn)()()()()()()()(01110111sRbssRbsRsbsRsbsYassYasYsasYsammmnnnn)s(Rb)s(sRb)s(Rsb)s(Rsb)s(Ya)s(sYa)s(Ysa)s(Ysa011m1mmm011n1nnn)()()()()()()()(01110111sRbssRbsRsbsRsbsYassYasYsasYsammmmmnnnn)()()()()()()()(1110111sRbssRbsRsbsRsbsYassYasYsasYsammmmmnnnn)()()()()()()()(01110111sRbssRbsRsbsRsbsYassYasCsasYsammmmnnnnnnnmmmmasasasabsbsbsbsRsCsG11101110)()()(根据传递函数的定义得系统的传递函数：例：试求RLC无源网络的传递函数。解：RLC无源网络的微分方程为：零初始条件下，方程两边取拉氏变换，得：由传递函数的定义得RLC无源网络的传递函数为：)()()()(22tutudttduRCdttudLCiooo)()()1(2sUsURCsLCsio11)()()(2RCsLCssUsUsGioRCui(t)uo(t)Li(t)练习1：已知系统的微分方程为)(2)(3)(5)(2)(322txdttdxtydttdydttyd52323)(2ssssG练习2：已知系统的传递函数为：求在单位阶跃输入作用下系统的输出响应c(t)。解答：6(3)()(1)(2)sGsss2）性质：①传递函数是复变量s的有理真分式函数，具有复变函数的所有性质，m≤n，且所有系数均为实数。②传递函数只取决于系统或元件的结构和参数，与输入量的形式无关，不反映系统内部的任何信息。故可用方框图表示：③传递函数与微分方程有相通性。即系数相对应。故零初始条件下，微分运算符与s可置换。G(s)R(s)C(s)212021)()()(asasabsbsRsCsG)()()()(212120sRbsbsCasasa)()()()()(2121220trbdttdrbtcadttdcadttcda④传递函数的拉氏反变换是脉冲响应g(t)。3）零初始条件的含义：①零初始条件含义：输入量是在时才作用于系统，因此在时，输入量及其各阶导数均为0；②输入量加入系统之前，系统处于稳态，输出量及其各阶导数在时为0。0t0t0t)]([)(1)]([)(1sCLtgtLsR)]()([1sRsGL)]([1sGL几个重要的拉氏变换f(t)F(s)f(t)F(s)δ(t)1sinwt1(t)1/scoswtt1/(s+a)21sate)(22wsw)(22wsswteatsinwteatcos22)(wasw22)(wasas2传递函数的零点和极点传递函数的分子多项式和分母多项式经因式分解后可写成：njjmiinmpszsKpspspsazszszsbsG11210210)()()())(()())(()(式中Zi是传递函数的零点，Pi是传递函数的极点。传递函数的零点和极点可以是实数也可以是复数。K=b0/a0是传递系数或根轨迹增益。传递函数的分子多项式和分母多项式经因式分解后也可写成如下因子连乘的形式：)1()12)(1()1()12)(1()(2222122221sTsTsTsTassssbsGjnim式中一次因子对应实数零极点，二次因子对应共轭复数零极点。、Tj为时间常数。K=bm/an是传递系数或增益。i例1：已知系统的传递函数为：)2)(1()3(6)(ssssG若输入为单位阶跃函数，即输入的象函数为，则s121)2)(1()3(6)()()(321sCsCsCsssssRsGsC3传递函数的零点和极点对输出的影响9)2)(1()3(6lim01sssssCs12)2)(1()1)(3(6lim12sssssCs3)1()3(6)2)(1()2)(3(6lim23ssssssssCstttteeeCeCCtc223213129)(结论：传递函数的极点就是微分方程的特征根，它决定了系统自由运动的模态。tteetc23129)(例2：具有相同极点但不同零点的传递函数分别为：极点相同都为-1，-2，G1(s)的零点为-0.5，G2(s)的零点为-1.33，它们的零极点分布图如图所示。在复平面上，一般用“”表示零点，用“”表示极点。)2s)(1s(2s4)s(G1)2s)(1s(2s5.1)s(G2–2-10jtteessssLtc211321)2)(1(24)(tteessssLtc2125.05.01)2)(1(25.1)(结论：传递函数的零点并不形成自由运动的模态，但他们却影响各模态在响应中所占的比重。因而也影响曲线的形状。零初始条件下它们的单位阶跃响应分别为：)2)(1(24)(1ssssG1、)2s)(1s(2s5.1)s(G22、G1的零点Z1接近原点，距两个极点较远，两个模态所占的比重大，Z1的作用明显；G2的零点Z2距原点较远，距两个极点均较近，两个模态所占的比重小，Z1的作用明显。–2-10j自学：单容水槽、双容水槽、电加热炉等4典型元部件的传递函数单容对象：V--1V--2h空调房间11)(TssGV--3V--4h1V--5h2HX-2送风热水热水加热器多容对象：由两个或多个单容对象之间通过某些关系联系在一起的对象。)1)(1()(21sTsTKsG双容水槽2-4控制系统的结构图与信号流图1系统结构图的组成与绘制1）组成：由对信号进行单向运算的方框和信号流向线所组成。包含四种基本单元：信号线、引出点、比较点、方框。控制系统的结构图是描述系统各环节之间信号传递关系的数学模型，它表示了系统各环节之间的因果关系以及对各变量进行的运算。是控制理论描述复杂系统的一种简便方法。信号线：带有箭头的直线，表示信号的流向，在直线旁标记信号的时间函数或象函数。u(t),U(s)u(t),U(s)u(t),U(s)引出点（或测量点）：表示信号引出或测量的位置。从同一位置引出的信号在数值和性质方面完全相同。u(t)U(s)c(t)C(s)G(s)u(t),U(s)r(t),R(s))()(trtu)s(R)s(U比较点（或综合点）：表示对两个以上的信号进行加减运算。方框（或环节）：表示对信号进行的数学变换。方框中写入环节的传递函数。2）绘制：例：绘制无源网络的结构图2.结构图的等效变换与简化1）串联连接：前一个环节的输出是后一个环节的输入。R(s)C(s)U(s))s(G1)s(G2)()()(1sRsUsG)()()(2sUsCsG)()()(sRsCsG结论：串联连接的传递函数为各个环节传递函数的乘积。)()()()(sUsRsCsU)()(21sGsG2）并联连接：输入量相同，输出量等于两个方框输出量的代数和。R(s)C(s))s(G1)s(G2)(1sC)(2sC)()()(11sRsCsG)()()(22sRsCsG)()()()()(2121sRsCsCsGsG)()()()()()()()(2121sGsGsRsXsXsRsCsG结论：并联连接的传递函数为各个环节传递函数的和。)()()()()()()()(2121sGsGsRsCsCsRsCsG)s(G)s(G)s(R)s(X)s(X)s(R)s(Y)s(G21213）反馈连接：以负反馈为例R(s)C(s)G(s)H(s)-B(s)E(s))s(B)s(R)s(E)()()()()()(sCsHsBsCsBsH)()()()()()(sGsCsEsEsCsG)()()()()(sCsHsRsGsC)()()()()(1sRsCsGsHsG)()()(sRsCsG)()()()()()(sGsCsEsEsCsG)()()()()()(sCsHsBsCsBsH)()(1)(sHsGsG闭环传递函数，常用表示Φ(s)表示。4）引出点和比较点的移动a.引出点前移GG)s(R)s(Y1)s(Y2G)s(R)s(Y1)s(Y2G)s(R)s(Y1)s(Y2b.引出点后移G)s(R)s(Y1)s(Y21/Gc.比较点前移d.比较点后移Y(s)G(s))s(R1)s(R2Y(s)G(s))s(R1)s(R2Y(s)G(s))s(R1)s(R21/G(s)Y(s)G(s))s(R1)s(R2G(s)举例例1.化简下列方框图，并求系统的传递函数。AB解：1.比较点A前移，引出点B后移。)]s(H)s(G)s(H)s(G)[s(G1)s(G)s(G)s(G)s(R)s(Y)s(G21132321)]s(H)s(G)s(H)s(G)[s(G1)s(G)s(G)s(G)s(R)s(Y)s(G211323212.串并联变换。3.反馈联接变换。举例：板书。复习3.信号流图的组成及性质信号流图起源于梅森（S.J.MASON）利用图示法来描述一个和一组线性代数方程，是由节点和支路组成的一种信号传递网络。（1）组成及性质节点：表示变量或信号，其值等于所有进入该节点的信号之和。支路：连接两个节点的定向线段，用支路增益（传递函数）表示方程式中两个变量的因果关系。支路相当于乘法器。信号在支路上沿箭头单向传递。RIU表示两节点一支路组成的信号流图。典型的信号流图：5个节点代表5个变量x1,x2,x3,x4,x5;支路增益1,a,b,c,d,e,f,g.左端的变量取决于右端有关变量的线性组合，信号流图把各变量之间的因果关系贯通了起来。（2）术语输入节点（源节点）：只有输出支路的节点，代表系统输入变量。输出节点（阱节点）：只有输入支路的节点，代表系统输出变量。混合节点：既有输出支路，又有输入支路的节点。前向通路：信号由输入节点到输出节点传递时，每个节点只通过一次的通路。如x1→x2→x3→x4→x5和x1→x2→x5。回路：起点就是终点，并且与其它节点相交不多于一次的闭合通路，如x2→x3→x2、x3→x4→x3、x5→x5不接触回路：回路之间没有公共节点。如x2→x3→x2与x5→x5x3→x4→x3与x5→x54.信号流图的绘制由系统结构图绘制信号流图：•结构图的信号线上用小圆圈标志出传递的信号，得到节点；•标有传递函数的线段代替方框，得到支路；•支路增益为1的相邻节点可以合并，源节点及阱节点除外；•比较点之前没有引出点时，在比较点之后设置一节点；•比较点之前有引出点时，在比较点和引出点各设一节点。例1e1e2e3e4e1e2e3e4例2G2G1G3HG4R+C+-e1e2e3G11G3G2-HG4R1C-He1e2e3G11G3G2G4R1C5.梅森增益公式Pk—第k条前向通路的传递函数（通路增益）—第k条前向通路特征式的余因子，即对于流图的特征式∆，将与第k条前向通路相接触的回路传递函数代以零值，余下的∆即为∆k。∆kP—源节点到阱节点的传递函数（总增益）。n为前向通路总数。nkkkPP11∆—流图特征式...1fedcbaLLLLLL—所有单独回路的传递函数之和aL—每两个互不接触回路传递函数乘积之和cbLL—每三个互不接触回路传递函数乘积之和fedLLL例1：只有一个前向通路的情况H2G1G2H1H3R-C--G3G4e1e2e3e4e1e2RG1C-H3-H2e3e4G2G4G3-H111）从源节点到阱节点只有一个前向通路，总增益e1e2RG1C-H3-H2e3e4G2G4G3-H1143211PGGGG2）有三个单独回路，回路增益分别为：2321LHGG3432LHGG143213LHGGGG3）没有不接触回路，且前向通路与所有回路均接触，故余因子式114）由梅森增益公式求得系统传递函数：111)()(pPsRsCRC1432134323243214321143213432321111HGGGGHGGHGGGGGGGGGGHGGGGHGGHGG1111pLa例2：有多个前向通路的情况()Rs()Cs1G2G3G4G5G6G7G1H2H+-++-++()Rs()Cs1G2G3G4G5G6G7G1H2H1()Rs()Cs1G2G3G4G5G6G7G1H2H13）从源节点到阱节点有三个前向通路：P1=G1G2G3G4G5Δ1=1P2=G1G6G4G5Δ2=1P3=G1G2G7Δ3=1-L11）有四个单独回路，回路增益分别为：L1=-G4H1L2=-G2G7H2L3=-G6G4G5H2L4=-G2G3G4G5H22）有一组互不接触回路，L1和L2。所以，流图特征式Δ=1-（L1+L2+L3+L4）+L1L24）由梅森增益公式求得系统传递函数：272142543225462721414721346154321332211HGGHGHGGGGHGGGHGGHG1)HG(1GGGGGGGGGGGG)ΔpΔpΔ(pΔ1R(s)C(s)e1→e2→e5→e1e3→e4→e3e1→e3→e4→e5→e1e1→e2→e3→e4→e5→e1R→e1→e2→e3→e4→e5→CR→e1→e3→e4→e5→CR→e1→e2→e5→Ce1e2e4e3e56.闭环系统的传递函数C(s)：输出信号；R(s)：有用输入信号；N(s)：扰动信号；E(s)：误差信号。典型反馈控制系统的结构图和信号流图H(s)R(s)-C(s)G1(s)G2(s)B(s)E(s)N(s)111RCEEN-HG1G2C（1）输入信号作用下的闭环传递函数H(s)R(s)-C(s)G1(s)G2(s)B(s)E(s)应用叠加原理，令N(s)=0，得)()()(1)()()()()(2121sHsGsGsGsGsRsCs进一步求得系统输出量为：)()()()(1)()()()()(2121sRsHsGsGsGsGsRssC（2）扰动作用下的闭环传递函数应用叠加原理，令R(s)=0，得)()()(1)()()()(212sHsGsGsGsNsCsn进一步求得系统输出量为：)()()()(1)()()()(212sNsHsGsGsGsNssCnH(s)-C(s)G1(s)G2(s)B(s)E(s)N(s)H(s)-C(s)G1(s)G2(s)N(s)R(s)和N(s)同时作用下的系统输出量为：)]()()()()([)()()(11)()()()()(22121sNsGsRsGsGsHsGsGsNssRssCn若》1，则)()()(21sHsGsG)()()(1)()(1)(1sNsHsGsRsHsC若》1，则)()(1sHsG)()(1)(sRsHsC在一定条件下，系统输出只取决于反馈通路的传递函数及输入信号，与前向通路的传递函数无关，不受扰动作用的影响。若=1，即单位反馈，则)(sH)()(sRsC输出近似实现了对输入信号的完全复现，对扰动具有较强的抑制能力。（3）闭环系统的误差传递函数)()()(11)()()(21sHsGsGsRsEse1RN11CEE-HG1G2C)()()(1)()()()()(212sHsGsGsHsGsNsEsen可以由梅森增益公式求得误差传递函数，注意前向通路的确定。1R1EE-HG1G2CN1EE-HG1G2C也可以将结构图等效变换后求闭环系统的误差传递函数•红色代表回路；•蓝色代表前向通道。闭环系统的开环传递函数)()()(1)()()()()(2121sHsGsGsGsGsRsCs)()()(1)()()()(212sHsGsGsGsNsCsn)()()(11)()()(21sHsGsGsRsEse)()()(1)()()()()(212sHsGsGsHsGsNsEsen闭环系统的开环传递函数：等效为主反馈断开时从输入信号R到反馈信号B的传递函数。H(s)R(s)-C(s)G1(s)G2(s)B(s)E(s)N(s)总结•拉氏变换及反变换定义，部分分式展开法•微分方程—时域数学模型通式、建立、求解•传递函数—复域数学模型定义、性质、两种写法•结构图与信号流图结构图化简、梅森公式•闭环传递函数与开环传递函数第三章线性系统的时域分析法所谓时域分析法，就是在时间域内研究控制系统性能的方法，它是通过拉氏变换直接求解系统的微分方程，得到系统的时间响应，然后根据响应表达式和响应曲线分析系统的动态性能和稳态性能。控制系统的时域性能指标，是根据系统在单位阶跃函数作用下的时间响应——单位阶跃响应确定的，通常以h（t）表示。3-1系统的时域性能指标1典型输入信号使用典型的输入信号只是为了分析和设计的方便。采用典型的输入信号，可以使问题的数学处理系统化，可以由此去推知更复杂输入下的系统响应。单位阶跃函数单位斜坡函数单位脉冲函数0001tt000ttt单位抛物线函数000212tttr(t)=r(t)=r(t)=R(s)=1/SR(s)=1/S2R(s)=1/S3r(t)=)t(t,0t,0t0,1lim0R(s)=1控制系统的时域性能指标，是根据系统在单位阶跃函数作用下的时间响应——单位阶跃响应确定的，通常以h（t）表示。2动态过程和稳态过程在典型输入信号作用下，任何一个控制系统的时间响应都由动态过程和稳态过程两部分组成。（1）动态过程系统在典型输入信号作用下，输出量从初始状态到最终状态的响应过程，又称过渡过程或瞬态过程。表现为衰减、发散、等幅振荡的形式。（2）稳态过程系统在典型输入信号作用下，当时间t→∞时输出量的表达方式，又称为稳态响应。一个实际的控制系统必须是衰减的（稳定的）。3动态性能和稳态性能在典型输入信号作用下，系统的性能指标由动态性能和稳态性能两部分组成。（1）动态性能动态性能指标：描述稳定的系统在单位阶跃函数作用下，动态过程随时间t的变化状况的指标。假设，零初始条件下，系统的单位阶跃响应h(t)如下，trtptsh(t))(h1.00误差带5%或2%td0.5其动态性能指标为：延迟时间td响应曲线首次达到稳态值的一半所需的时间。上升时间tr响应曲线从零首次上升到稳态值h(∞)所需的时间，称为上升时间。对于响应曲线无振荡的系统，tr是响应曲线从稳态值的10%上升到90%所需的时间。峰值时间tp响应曲线超过稳态值h(∞)达到第一个峰值所需的时间。调节时间ts在稳态值h(∞)附近取一误差带，通常取响应曲线开始进入并保持在误差带内所需的最小时间，称为调节时间。ts越小，说明系统从一个平衡状态过渡到另一个平衡状态所需的时间越短。其动态性能指标为：超调量σ%响应曲线超出稳态值的最大偏差与稳态值之比。即%100)()()(%hhthp超调量表示系统响应过冲的程度，超调量大，不仅使系统中的各个元件处于恶劣的工作条件下，而且使调节时间加长。tr,tp和ts表示控制系统反映输入信号的快速性，而σ%反映系统动态过程的平稳性。即系统的阻尼程度。其中ts和σ%是最重要的两个动态性能的指标。（2）稳态性能稳态误差：当时间t→∞时系统的输出量不等于输入量或输入量的确定函数，则系统存在稳态误差，通常在阶跃函数、斜坡函数或加速度函数作用下进行测定或计算。•结论：动态性能指标反映了系统的响应速度和阻尼程度，稳态性能指标反映了系统的控制精度。3-2一阶系统的时域分析1一阶系统的数学模型什么是一阶系统？①以一阶微分方程作为运动方程②闭环传递函数11)()()(TssRsCs2一阶系统的单位阶跃响应r(t)=1(t)微分方程：)()()(trthdttdhTTteth/1)(Ts1C(s)R(s)可查表2-3（23）一阶系统的单位阶跃响应曲线为初始值为零，以指数规律上升到终值的曲线。t0.51.03TT0h(t)0.6320.950.8651）时间常数T可度量输出量的数值，如h(T)=0.632。t=3T-4T时过渡过程基本结束。此特点可用于测定T的数值或判断系统是否为一阶系统。2）时间常数T是阶跃响应曲线在t=0处切线斜率的倒数。随时间的推移斜率逐渐下降。TeTdttdhttTt11)(00•结论：时间常数T决定了曲线的形状，反映了系统的惯性；T越小，系统惯性越小，响应过程越快。一阶系统的动态性能指标为：tp和σ%不存在。TtTtTtsrd320.269.0t0.51.03TT0h(t)0.6320.950.8653一阶系统的单位脉冲响应：r(t)=(t)则R(s)=1TteTTsLLtC/1]11[]C(s)[)(G(s)C(s)11响应曲线为单调下降的指数曲线。ts=3T。实际中常以单位脉冲输入信号作用于系统，根据被测系统的单位脉冲响应求得被测系统的闭环传递函数。4一阶系统的单位斜坡响应：r(t)=t则R(s)=1/s2单位斜坡响应为)0(/)(]111[]C(s)[)(211tTteTTtsTsLLtc稳态分量：斜率与输入信号相同时间滞后T的斜坡函数。瞬态分量：衰减的非周期函数。tTr(t)=tc(t)02TT-T一阶系统单位斜坡响应存在稳态误差ess=t-(t-T)=T从曲线上可知，一阶系统单位斜坡响应达到稳态时具有和输入相同的斜率，只是在时间上滞后T,这就存在着ess=T的稳态误差。5一阶系统的单位加速度响应：单位加速度响应为)0(/),1(21)(22tTteTTtttc结论：系统对输入信号导数的响应就等于系统对该输入信号响应的导数；系统对输入信号积分的响应就等于系统对该输入信号响应的积分；积分常数由零输出初始条件确定。31)(,21)(2ssRttr输出响应输入信号一阶系统对典型输入信号的输出响应)0(/)1(2122tTteTTtt221tt)(1t)(t)0(/1tTte)0(/tTteTTt)0(/1tTteT3-3二阶系统的时域分析1二阶系统的数学模型什么是二阶系统？①以二阶微分方程作为运动方程②闭环传递函数1212)()((s)2222TssTsssRsCnnn方框图其中ζ——系统的阻尼比ωn——系统的无阻尼自然振荡角频率——系统振荡周期nT102)(22nnsssD特征方程122,1nns特征根（1），具有一对正实部的特征根，系统为发散振荡。0（2），具有一对纯虚根，系统等幅振荡。0（3），系统为一对共轭复根，为衰减振荡。10（4），系统有两个相等的负实根，为非周期过程，临界阻尼。1（5），系统有两个不相等的负实根，系统也是非周期过程，为过阻尼情况。1122,1nnsζ的大小不同决定了二阶系统特征根具有不同的性质。根位置不同（、n不同）有不同的阶跃响应001011不等负实根1相等负实根2共轭复根3共轭虚根4正（正实部）根5根在根平面上的位置ImRe101253344122,1nns2二阶系统的单位阶跃响应1）欠阻尼（0<ζ<1）二阶系统的单位阶跃响应22,11nnjs若令则dndnjs2,121,衰减系数阻尼振荡频率0)sin(1)1sin(1)(222111211ttearctgtethdtntnn21,21arctgnd其中：当r(t)=1,即R(s)=1/s时对上式整理并取拉式反变换得单位阶跃响应:sssCnnn12(s)222ζ=0时，无衰减，等幅振荡。nd,0无阻尼振荡频率，又叫自然频率ζ=02）临界阻尼（ζ=1）二阶系统的单位阶跃响应当r(t)=1,即R(s)=1/s时对上式整理并取拉式反变换得单位阶跃响应:sssCnnn12(s)2220)1(1)(tttethnn•阶跃响应是随时间单调上升的•当t∞响应趋于稳态值3）过阻尼（ζ>1）二阶系统的单位阶跃响应当r(t)=1,即R(s)=1/s时)/1)(/1((s)212TsTssCn01/1/1)(21122/1/tTTeTTethTtTt其中T1，T2称为过阻尼二阶系统的时间常数，且T1>T2，对上式取拉式反变换得单位阶跃响应:)1(1,)1(12221nnTT通常取ζ=0.4-0.8为宜。3欠阻尼（0<ζ<1）二阶系统的动态过程分析动态性能指标的计算1）延迟时间td的计算td不能用ζ和ωn准确描述，采用工程上的近似计算方法得到：)10(7.01ndtndt22.06.01增大ωn或减小ζ都可以减小延迟时间。)sin(1)(211tethdtn2）上升延迟时间tr的计算根据定义，有振荡的系统上升时间为响应从零第一次上升到终值所需的时间。因此，令h(tr)=1，得：当阻尼比ζ一定时，阻尼角β不变，系统响应速度与ωn成正比；当阻尼振荡频率ωd一定时，阻尼比越小上升时间越短。)sin(1)(211tethdtn0)sin(211tedtn0211rnte0)sin(rdtrdtdrt！第一次到达21,21arctgnd3）峰值时间tp的计算对上式求导并令其为零，整理后得：)sin(1)(211tethdtn21,21arctgnd0)(ptdttdhdpt！第一次到达21)(pdttg21tgarctpd4）超调量σ%的计算根据超调量的定义得：)sin(1)(211tethdtn%100)sin(1%100)()()(%21pdtPtehhthpndpt%100%21e21sin)sin()sin(pdtCos21Sinnnd21,21arctgnd%100%21e只与阻尼比有关0ζ1.0σ%100%一般选取ζ=0.4-0.8时，σ%介于1.5%-25.4%之间。5）调节时间ts的计算)sin(1)(211tethdtn)(1sth11Ts很难用ζ和ωn准确描述，采用工程上的近似计算方法得到：)05.0(5.35.3nst)02.0(4.44.4nst4过阻尼二阶系统的动态过程分析（含临界阻尼）单调过程，动态性能指标中σ%,tp无意义，td，tr，ts采用工程上的近似计算方法得到：)1(2.06.012ndt根据过阻尼二阶系统的单位阶跃响应，若令T1大于或等于4T2，则：)1(5.112nrt)1(75.4)1(311TtTtss5二阶系统性能的改善1）比例-微分控制比例-微分控制是一种早期控制，可在产生位置误差前提前产生修正作用，从而达到改善系统性能的目的)2(2nnss1TdsR(s)C(s)-++E(s)系统开环传递函数2,)12()1()2()1()(2nndndnksssTksssTsG22222222)1(2)1()(1)()(nnddnndnndnsssTsTsssTsGsGs闭环传递函数:nddT21等效阻尼比：•相当于给系统增加了一个闭环零点，比例-微分控制的二阶系统称为有零点的二阶系统。•比例-微分控制不改变系统的自然频率但可增大阻尼比，故可抑制系统的振荡。增大了系统的阻尼比,可以使系统动态过程的超调量下降,调节时间缩短,然而开环增益k保持不变,它的引入并不影响系统的稳态精度,同时也不改变系统的无阻尼振荡频率wn。比例微分控制使系统增加了一个闭环零点s=-1/Td，前面给出的计算动态性能指标的公式不再适用。由于稳态误差与开环增益成反比,因此适当选择开环增益和微分器的时间常数Td,即可减小稳态误差,又可获得良好的动态性能。d5二阶系统性能的改善2）测速反馈控制)2(2nnss)(sER(s)C(s)--kts)12()(2ntnkssksG开环传递函数为系统的开环增益。k有所减小,增大了稳态误差,因此降低了系统的精度。)2(ntnkk闭环传递函数显然，所以速度反馈同样可以增大系统的阻尼比,而不改变无阻尼振荡频率wn,因此,速度反馈可以改善系统的动态性能。2222)(nntnwswswsnttwk21等效阻尼比：t在应用速度反馈校正时,应适当增大原系统的开环增益,以补偿速度反馈引起的开环增益减小,同时适当选择速度反馈系数kt,使阻尼比ξt增至适当数值,以减小系统的超调量,提高系统的响应速度,使系统满足各项性能指标的要求。3-5线性系统的稳定性分析1稳定性的基本概念abcb如小球的位置在a或c点,在微小扰动下,一旦偏离平衡位置,则无论怎样,小球再也回不到原来位置,则是不稳定的。如小球平衡位置b点,受外界扰动作用,从b点到点，外力作用去掉后,小球围绕b点作几次反复振荡,最后又回到b点,这时小球的运动是稳定的。b稳定的定义若线性控制系统在初始扰动的影响下，其动态过程随时间的推移逐渐衰减并趋于0（原平衡工作点）则称系统为稳定，反之若在初始扰动的影响下，其动态过程随时间的推移而发散，则称系统不稳定。系统的稳定性与外作用及初始条件无关，取决于系统本身的结构参数，是系统的固有特性。2线性系统稳定的充分必要条件闭环系统特征方程的所有根均具有负实部；或者说闭环传递函数的极点均严格位于左半s平面。R(s)C(s)G(s)H(s)-)()(1)()()()(sHsGsGsRsCs0)s(H)s(G1闭环系统的特征方程为：如果能够求出特征方程的所有根，则很容易判断系统的稳定性。例：已知求系统的稳定性。02.211)1s02.0)(1s01.0(s解得：)1s02.0)(1s01.0(s2.211)s(G1)s(HR(s)C(s)G(s)H(s)-0)1s02.0)(1s01.0(s2.21110)s(H)s(G1解：根据闭环系统的特征方程：即：010056.1s5000s150s6230)6600s10s)(160s(2160s1263j5s3,23劳斯稳定判据不用直接求出特征根，而依据特征方程的系数来判断线性系统的特征根是否全部严格位于左半s平面。则使线性系统稳定的充分必要条件是：在上述特征方程中，各项系数均为正数。设线性系统的特征方程为：0,0)(01110aasasasasDnnnn充分必要条件是可由劳斯稳定判据获得，劳斯稳定判据为表格形式，称为劳斯表。321nnnnssss0a2a4a1302113aaaaac1504123aaaaac1323131314ccaacc321nnnnssss321nnnnssss321nnnnssss321nnnnssss1a13c14cnnnncbaa13a23c24c2232nnnncbaa5a33c454nnnbaa4n5n4nbaa0,0)(01110aasasasasDnnnn01ssnc,11,1ncnnac1,1线性系统稳定的充分必要条件：劳斯表第一列各值为正。如果劳斯表第一列中出现小于零的数值，系统不稳定，且变号的次数等于特征方程正实部根的数目。例：已知系统的特征方程如下，试用劳斯稳定判据判断该系统的稳定性。05432234ssss解：该系统劳斯表为：由于劳斯表的第一列系数有两次变号，故该系统不稳定，且有两个正实部根。S4135S2S1S0S324124132561524154劳斯稳定判据的特殊情况1）劳斯表中某行第一列项为零，其余各项不为零或不全为零。例：已知系统的特征方程如下，试用劳斯稳定判据判断该系统的稳定性。014222345sssss解：该系统劳斯表为：S5121S300.5S4241方法：用一个很小的正数代替它，继续进行运算，直至计算结束，然后在的条件下判断第一列中各元素的符号。0S2∞,014,0所以，劳斯表第一列变号两次，系统不稳定。S30.5S2114↓↓↓S10.5S01S300.50S5121S42412）劳斯表中出现全零行。例：已知系统的特征方程如下，试用劳斯稳定判据判断该系统的稳定性。04473223456ssssss解：该系统劳斯表为：S61-2-7-4S41-3-4S51-3-4方法：根据全零行的上一行系数构造一个辅助方程F(s)=0，以该方程对s求导，导数方程的系数代替劳斯表的全零行，继续计算。S3000说明特征方程有一些根位于虚轴上，系统处于临界状态，不稳定。其它根的情况由以下方法判断。043)(24sssF辅助方程：S34-6S2-1.5-4↓↓S1-16.70S0-40643ss求导：S61-2-7-4S41-3-4S51-3-4S3000劳斯表第一列数值有一次变号，系统不稳定，且有一个正实部根。特征根的情况：纯虚根±j，其它根±2，2/)31(j5劳斯稳定判据的应用1）确定系统稳定时的参数取值范围2）确定系统稳定裕量用(S-σ)代替S，如果用劳斯判据判断仍能稳定，则表明该系统至少有稳定裕量σ。带参数按步骤列表计算劳斯表第一列元素；令含参数的元素大于零，得到系统稳定时的参数取值范围。注意：劳斯稳定判据的应用只局限于判断系统的稳定性。若稳定，不能保证有好的动态性能；若不稳定，不能给出使其稳定的方法。例：求当系统稳定时k值的范围。ksssks2)(230223ksss解：系统的闭环传递函数：特征方程：劳斯表：S312S21kS12-k0S0k002kk如果系统稳定，则有20k解得：0223ksss特征方程：课堂练习：已知单位反馈控制系统的开环传递函数为试确定系统稳定时的K值范围。)15.0)(1()15.0()(2sssssKsG71.10K3-6线性系统的稳态误差计算1稳态误差的定义R(s)C(s)G(s)H(s)-B(s)E(s)R(s)1G(s)H(s)-B(s)E(s))()()()()()(sHsCsRsBsRsE当主反馈信号B(s)与输入信号不等时，比较装置的输出)()(11)()()(sHsGsRsEse闭环系统的误差传递函数误差信号E(s)的时域表达式)]()([)]([)(11sRsLsELteee(t)包含瞬态分量ets(t)和稳态分量ess(t)两部分。0)(ttste因为所以，稳态误差的定义为误差信号e(t)的稳态分量ess(∞)，常以ess简单表示。)(1)(lim)(lim)(lim)(lim000sGssRssEteteesstss)(1)(lim)(lim)(lim)(lim000sGssRssEteteesstss)(1)(lim)(lim)(lim)(lim000sGssRssEteteesstss)()(1)(lim)(lim)(lim)(lim00sHsGssRssEteteesstss——稳态误差的基本公式计算方法之一如果sE(s)的极点均位于s左半平面(包括原点)，则可根据拉氏变换的终值定理求得稳态误差：例：设单位反馈控制系统的开环传递函数为G(s)=1/Ts,输入信号为r(t)=t2/2，试求控制系统的稳态误差。解：系统的误差传递函数为)/1(1)(2TsssE当r(t)=t2/2时，R(s)=1/s3)()(11)()()(sHsGsRsEseTsTsTsT/1222Ts1112/2)]([)(1TTteTsELteTt瞬态分量ets(t)随时间增长衰减至零。稳态分量ess(t)随时间增长趋于∞。sE(s)在s=0处有一个极点，另一个极点为-1/T。)/1(1)(TssssE)/1(1lim)(lim)(lim00TssssEteesstss根据拉氏变换的终值定理，得2系统类型设一般情况下分子阶次为m,分母阶次为n的开环传递函数可表示为njjmiisTssKsHsG11)1()1()()(K是开环增益。、Tj为时间常数。V为开环系统在s平面坐标原点上的极点的重数。i系统类型的定义：当V=0时为0型系统，当V=1为Ⅰ型系统，当V=2时，为Ⅱ型系统。当s→0时njjmiisTssKsHsG11)1()1()()(受系统类型、开环增益、输入信号的影响。可以根据已知的输入信号的形式迅速判断系统是否存在原理性稳态误差及稳态误差的大小。描述了控制系统跟踪不同输入信号的能力。1)1()1(11njjmiisTs故s→0时sKsHsGs0lim)()(sksRsskssRsHsGssRessssss01000lim)]([lim1)(lim)()(1)(lim故——稳态误差的计算通式计算方法之二3阶跃输入作用下的稳态误差与静态位置误差系数由稳态误差的计算通式得各型系统在阶跃输入信号作用下的稳态误差为：R(s)C(s)G(s)H(s)-B(s)E(s)sRsRtRtr/)()(1)(100)1/()(，，KRess0型单位反馈控制系统在阶跃输入作用下的稳态误差描述的是输出的希望值与实际值的位置误差。如果要求系统对于阶跃输入作用不存在稳态误差，则必须选用Ⅰ型及Ⅰ型以上的系统。时当sRsRtRtr/)()(1)(习惯上常采用静态位置误差系数Kp表示各系统在阶跃输入作用下的位置误差。p00K1)()(lim1)()(1)(limRsHsGRsHsGssRessss）（称为静态位置误差系数。)()(limK0psHsGs10，，KKp各型系统的静态位置误差系数为：sKsHsGs0lim)()(4斜坡输入作用下的稳态误差与静态速度误差系数由稳态误差的计算通式得各型系统在斜坡输入信号作用下的稳态误差为：R(s)C(s)G(s)H(s)-B(s)E(s)2/)()(sRsRtRtr201/0)(，，，KRess时当2/)()(sRsRtRtr习惯上常采用静态速度误差系数KV表示各系统在斜坡输入作用下的位置误差。v00K)()(lim)()(1)(limRsHssGRsHsGssRessss）（称为静态位置速度误差系数。100vlim)()(limKsKsHssGss2100，，，KKv各型系统的静态速度误差系数为：sKsHsGs0lim)()(5加速度输入作用下的稳态误差与静态加速度误差系数由稳态误差的计算通式得各型系统在加速度输入信号作用下的稳态误差为：R(s)C(s)G(s)H(s)-B(s)E(s)32/)(2/)(sRsRtRtr302/1,0)(，，，KRess时当32/)(2/)(sRsRtRtr习惯上常采用静态加速度误差系数Ka表示各系统在加速度输入作用下的位置误差。a200K)()(lim)()(1)(limRsHsGsRsHsGssRessss）（称为静态位置加速度误差系数。2020alim)()(limKsKsHsGsss321,00，，，KKv各型系统的静态加速度误差系数为：sKsHsGs0lim)()(结论:（1）0型系统在阶跃信号作用下必有稳态误差，称为有差系统，1型、2型系统在阶跃信号作用下没有稳态误差，称为无差系统。1/K002型系统∞1/K01型系统∞∞1/(1+K)0型系统单位抛物线r(t)=t2/2单位斜坡r(t)=t单位阶跃r(t)=1稳态输入误差信号系统类型结论:（2）0型系统不能跟踪恒速变化的信号，1型系统能够跟踪恒速变化信号，但有稳态误差。2型系统能够跟踪恒速变化的信号，且无差。1/K002型系统∞1/K01型系统∞∞1/(1+K)0型系统单位抛物线r(t)=t2/2单位斜坡r(t)=t单位阶跃r(t)=1稳态输入误差信号系统类型结论:（3）0型、1型系统都不能跟踪恒加速度信号，2型系统能够跟踪恒加速度信号，但有差。1/K002型系统∞1/K01型系统∞∞1/(1+K)0型系统单位抛物线r(t)=t2/2单位斜坡r(t)=t单位阶跃r(t)=1稳态输入误差信号系统类型1型系统的单位斜坡响应2型系统的单位抛物线响应如果系统承受的输入信号是多种典型函数的组合，如2/)(1)(2210tRtRtRtr根据叠加性原理，可将每一输入信号单独作用于系统，再将各稳态误差分量叠加起来，得avpssKRKRKRe2101)(6扰动作用下的稳态误差控制系统在扰动作用下的稳态误差值反映了系统的抗干扰能力。理想情况下，系统任意形式的扰动作用下的稳态误差为零。R(s)C(s)G1(s)H(s)-B(s)E(s)G2(s)N(s)++当sEn(s)在s右半平面及虚轴上解析时)(lim)(0ssEensnss)()()()(1)()()(212sNsHsGsGsGsCsEnn例：设比例控制系统如下图所示，图中R(s)=R0/s为阶跃输入信号；M为比例控制器输出转矩，用以改变被控对象的位置；N(s)=n0/s为阶跃扰动转矩。试求系统的稳态误差。解：本系统为Ⅰ型系统。令N(s)=0,则系统对阶跃输入信号的稳态误差为零。令R(s)=0,则系统在扰动作用下的输出的实际值为)()1()(2122sNKKsTsKsCnR(s)C(s)K1-E(s)N(s)++)1(22sTsK扰动作用下输出的希望值为零，因此误差信号为100)(lim)(KnssEensnss)()1()()(2122sNKKsTsKsCsEnn系统在阶跃扰动转矩作用下的稳态误差为小测验1.化简方框图，求系统传递函数。2.单位负反馈系统结构图如下图所示，若输入信号分别为单位阶跃信号和单位斜坡信号，试求系统的稳态误差。11.0100ss1Rs+Ys_第三章线性系统的时域分析法7减小或消除稳态误差的措施1）增大系统开环增益，可减小输入信号r(t)作用下的稳态误差。1/K002型系统∞1/K01型系统∞∞1/(1+K)0型系统单位抛物线r(t)=t2/2单位斜坡r(t)=t单位阶跃r(t)=1稳态输入误差信号系统类型2）增大扰动作用点之前系统的前向通道增益，可以减小扰动信号n(t)作用下的稳态误差。R(s)C(s)K1-E(s)N(s)++)1(22sTsK100)(lim)(KnssEensnss3）在系统的前向通道设置串联积分环节。R(s)C(s)H(s)-B(s)E(s)G(s)s11/K002型系统∞1/K01型系统∞∞1/(1+K)0型系统单位抛物线r(t)=t2/2单位斜坡r(t)=t单位阶跃r(t)=1稳态输入误差信号系统类型R(s)C(s)H(s)-B(s)E(s)G(s)开环传递函数：G(s)H(s)开环传递函数：G(s)H(s)s1sTI1相当于提高系统的型号，可以消除r(t)作用下的稳态误差。4）在扰动作用点之前系统的前向通道或主反馈通道设置积分环节，可以消除n(t)作用下的稳态误差。r(t)=0-C(t)12Tsk)(1)(0tntn0ksk1(a)000210210)1(1)1(limknsnTsskkkTsskksesss改变扰动作用点的位置：r(t)=0-C(t)12Tsk)(1)(0tntn0ksk1(b)0)1(11lim021020snTsskkkTsksesss在扰动作用点之前的前向通路中增加一个积分环节用（比例积分调节器）代替。)11(00sTk0kr(t)=0-C(t)12Tsk)(1)(0tntnsk1(c))11(00sTk0)1()11(1)1(lim02100210snTsskksTkTsskksesss则注意在反馈控制系统中，增大开环增益或设置串联积分环节可以减小或消除系统的稳态误差，但会降低系统稳定性，甚至造成不稳定，恶化系统的动态性能。5）采用串级控制抑制内回路的扰动。串级控制系统不仅能迅速克服作用于副回路的干扰，对作用于主回路的干扰也有加速调节的作用。在调节过程中，副调节器具有先调、快调、粗调的特点，主调节器具有后调、慢调、细调的特点。串级控制系统对克服副回路的干扰有较强的能力。当干扰包括在副回路，干扰对主控变量的影响减弱为原来的22211pvcmGGGG热交换器传热量的控制如果一次侧蒸汽的压力较平稳，通常以供水温度作为被控参数，蒸汽流量作为操作量，可采用简单的单回路控制系统对热交换器的传热量进行控制。如果一次侧蒸汽的压力波动较大，需采用供水温度－蒸汽压力串级控制系统。特点：增加了副回路调节－蒸汽流量调节回路，能及时克服蒸汽压力波动对控制系统的影响，具有一定的自适应特性，能超前调节。主回路的定值调节与副回路的随动调节相互配合，协调工作，能提高系统的控制品质，满足供热工艺的要求。第四章线性系统的根轨迹法4-1根轨迹法的基本概念1根轨迹概念根轨迹简称根迹，是开环系统的某一参数从零变化到无穷时，闭环系统特征方程式的根在s平面上变化的轨迹。系统闭环特征方程为：D(s)=S2+2S+2K=0特征根为：S1,S2=-1±K21)15.0(ssKR(s)C(s)设控制系统如右图所示令K从0到无穷变化，可以用解析的方法求出特征根的全部数值。S1,S2=-1±K21将这些数值标注在S平面上，并连成光滑的粗实线。—系统闭环根轨迹根K00→0.50.50.5→∞∞S1=-1+K2100→-1-1-1+-1+j∞S2=-1-K21-2-2→-1-1-1--1-j∞12Kj12Kj重根共轭复根两根对称实根K=0.5K=∞K=∞K=0K=0-1-2根轨迹提供的信息：1、K从0→∞变化，根轨迹不会进入右半平面。即：无论如何该系统是稳定的。如果有可能越过虚轴进入右半平面，则与虚轴交点处的K值是临界开环增益，因此可由根轨迹图确定使系统稳定的K值取值范围。3、00.5时，根轨迹进入复平面，欠阻尼，阶跃响应为振荡过程，K越大振荡越厉害（ζ小）、振荡频率越高（ωd大）。K=0.5K=∞K=∞K=0K=0-1-2（2根轨迹与系统性能）（稳定性）2、以右图为例，开环系统在坐标原点有一个极点，属于Ⅰ型系统，此时根轨迹上的K值就是静态速度误差系数，如果给定系统的稳态误差要求，则由根轨迹图就可确定闭环极点位置的容许范围。（稳态性能）（动态性能）001011不等负实根1相等负实根2共轭复根3共轭虚根4正（正实部）根5根在根平面上的位置ImRe101253344122,1nns3闭环零极点与开环零极点之间的关系qiifiiGGpszsKsTsTsTssssKsG11222221212221)()()12)(1()12)(1()(前向通路的增益前向通路的根轨迹增益221221TTKKGG如图所示，控制系统的闭环传递函数为：将前向通路的传递函数和反馈通路的传递函数分别表示：)()(1)()()()(sHsGsGsRsCshjjljjHpszsKsH11)()()(同理R(s)C(s)G(s)H(s)-系统的开环传递函数可表示为：qihjjifiljjipspszszsKsHsG1111)()()()()()(K=KG·KH，称为开环系统的根轨迹增益。对于一个有m个开环零点和n个开环极点的系统，有f+l=m，q+h=n。系统的闭环传递函数为：nimjjifihjjiGzsKpspszsKs1111)()()()()(返回由系统的开环传递函数和闭环传递函数的表达式可得到以下结论：——闭环零极点与开环零极点之间的关系。1.闭环系统的根轨迹增益，等于开环系统前向通路的根轨迹增益。对于单位反馈系统，闭环系统根轨迹增益就等于开环系统根轨迹增益。2.闭环零点由开环前向通路传递函数的零点和反馈通路传递函数的极点所组成。对于单位反馈系统闭环零点就是开环零点。3.闭环极点与开环零点、开环极点和根轨迹增益K均有关。4根轨迹方程（绘制根轨迹的基本条件）设控制系统的闭环传递函数为：)()(1)()()()(sHsGsGsRsCs该系统的闭环特征方程为：1)()(0)()(1sHsGsHsG即当系统有m个开环零点和n个开环极点时：1)()()()(11niimjjpszsKsHsGzj为已知的开环零点，pi为已知的开环极点。当K从零变到无穷。——根轨迹方程绘制根轨迹的基本条件为了使用方便，根轨迹方程可由如下两个方程描述：2,1,0,)12)()(11kkpszsniimjj（mjjniizspsK11,2,1,011)12(kekj-1θ和相角条件幅值条件确定根轨迹的充要条件1)()()()(11niimjjpszsKsHsGKbadc幅角应满足：)12(4321k幅值应满足：z2z1P1P2abcdjSa4-2常规根轨迹的绘制法则法则1：根轨迹的起点和终点根轨迹起于开环极点，终于开环零点。根据绘制根轨迹的两个基本条件，演绎出八条绘制根轨迹的基本法则。根轨迹起点是指根轨迹增益K=0时的根轨迹点；根轨迹终点是指根轨迹增益K→∞时的根轨迹点。系统的闭环传递函数为：nimjjifihjjiGzsKpspszsKs1111)()()()()(s=zj；j=1,2,…,m。说明闭环特征根就是开环零点，所以根轨迹必终于开环零点。当K=0时：s=pi；i=1,2,…,n。说明闭环特征根就是开环极点，所以根轨迹必起于开环极点。闭环特征方程为：0)()(11nimjjizsKps当K→∞时：0)()(111nimjjizspsK在实际系统中，开环传递函数分子多项式的次数m与分母多项式的次数n满足m≤n，即零点个数≤极点个数。若有限数值的零点称为有限零点，无限数值的零点称为无限零点，则此时开环零极点的个数是相等的。m＜n时，n条轨迹从开环极点出发，只能有m条终止在开环零点,另外n-m条应终止何处？–2-10j——终止在无穷远处法则2：根轨迹的分支数、对称性和连续性。根轨迹的分支数等于有限零点数m和有限极点数n中的大者，连续且对称于实轴。法则3：根轨迹的渐近线。当开环有限极点数n大于有限零点数m时，有n-m条根轨迹分支沿着与实轴夹角为φa，交点为σa的一组渐近线趋向无穷远处，且有：1,,2,1,0;)12(mnkmnkamnzpmjjniia11渐近线的做法：设控制系统如上图所示，开环环传递函数为：R(s)C(s)-)22)(4()1(2sssssK)22)(4()1()()(2sssssKsHsG首先，根据已知的三个绘制法则，确定相关数据：开环零点z1=-1，开环极点p1=0，p2=-4，p3=-1+j，p4=-1-j，标注在s平面上。渐近线的做法：由法则1，根轨迹起于极点p1…p4，终于零点z1和无穷远处。由法则2，根轨迹有4条分支，连续且对称与实轴。由法则3，根轨迹有3条渐近线。夹角：2,3001,1800,60)12(000kkkmnka交点：67.1141mnzpiiaj0-4-1-1.6760°180°300°法则4：根轨迹在实轴上的分布。在实轴上的某一区域，若其右边开环实数零极点个数之和为奇数，则该区域必是根轨迹。j0-4-1-1.67法则5：根轨迹的分离点与分离角。两条或两条以上的根轨迹分支在s平面上相遇又立即分开的点称为根轨迹的分离点。其坐标是下列方程的解：niimjjpdzd1111zj、pi代表各开环零极点的数值。分离角为：)1,,1,0()12(lklkl为根轨迹相遇又分离的条数。有关分离点的说明：•分离的位于实轴上，或以共轭的形式成对出现在复平面中。•如果根轨迹位于实轴上两个相邻开环极点之间（其中一个可以是无限极点），这两个极点之间至少存在一个分离点。•如果根轨迹位于实轴上两个相邻开环零点点之间（其中一个可以是无限零点），这两个零点之间至少存在一个分离点。分离角代表根轨迹进入分离点的切线方向与离开分离点的切线方向的夹角。l=2时分离角为直角。例4-1设系统结构图如右图所示，试绘制其概略根轨迹。)3)(2()1(ssssKR(s)C(s)-j0-3-1-2解：将开环零极点标注在s平面上。由法则4知，实轴上区域[-3,-2]、[-1,0]是根轨迹的一部分。由法则2知，有3条根轨迹分支。由法则1知，有1条根轨迹起开环极点0，终于开环零点-1；另外2条分别起于开环极点-2，-3，终于∞。由法则3知，2条终于∞的根轨迹的渐近线与实轴的夹角和交点为：00270901,0;13)12()12(、即kkmnka213)1()]3()2(0[11mnzpmjjniia例4-1设系统结构图如右图所示，试绘制其概略根轨迹。)3)(2()1(ssssKR(s)C(s)-由法则5知，[-2,-3]之间必有一分离点d。j0-3-1-2)3(1)2(101)1(11111ddddpdzdniimjj因为d在[-2,-3]之间，用试探法，设d=-2.5左边略小于右边，重取d=-2.47两边近似相等。4.03121167.011dddd分离角为直角。概略根轨迹如右图所示。-2.47法则6：根轨迹起始角和终值角。根轨迹离开开环复数极点处的切线与正实轴的夹角，称为起始角，以标志。ip根轨迹进入开环复数零点处的切线与正实轴的夹角，称为终值角，以标志。iz,2,1,0)()12(1kknijppmjpzpijiji某一开环复数极点zj到pi的向量相角pj到pi的向量相角,2,1,0)()12(1kknjzpmijzzzijiji某一开环复数零点zj到zi的向量相角pj到zi的向量相角例4-3设系统开环传递函数如下，试绘制概略根轨迹。)5.15.0)(5.15.0)(5.2()2)(2)(5.1()(jsjsssjsjssKsG解：将开环零极点标注在s平面上。由法则4，确定实轴上的根轨迹[-∞,-2.5]、[-1.5,0]。由法则2，确定有4条根轨迹分支。由法则1，确定根轨迹起点和终点。由法则3，确定根轨迹有1条渐近线34)12(ka23411mjjniiazpj0-3-1-2由法则5，确定分离点。（本例无分离点）由法则6，确定起始角和终止角。①起始角作各开环零极点到开环复数极点（-0.5+1.5j）的向量，测出相应的角度。故开环复数极点（-0.5+1.5j）处的起始角为：0043132179101)12()()()12(2kkp根据根轨迹的对称性开环复数极点（-0.5-1.5j）处的起始角为：-790。2p②终止角作各开环零极点到开环复数零点（-2+j）的向量，测出相应的角度。故开环复数零点（-2+j）处的终止角为：025.149z根据根轨迹的对称性开环复数零点（-2-j）处的起始角为：-149.50。法则7：根轨迹与虚轴的交点。若根轨迹与虚轴相交，则交点上的K值与ω值可以用劳斯判据确定；也可令闭环特征方程中的s=jω，然后分别令其实部和虚部为零而求得。先令劳斯表第一列中包含K的项为零，即可确定K的值，即K取此值时根轨迹与虚轴相交。其次构造辅助方程，通常是利用s2行的系数构造辅助方程（一对纯虚根），求出的ω数值；如果有多对纯虚根，则采用幂大于2的s偶次方行的系数构造辅助方程。例4-4设系统开环传递函数如下，试绘制概略根轨迹。)22)(3()(2ssssKsG解：将开环零极点标注在s平面上。由法则4，确定实轴上的根轨迹[-3,0]。由法则2，确定有4条根轨迹分支。由法则1，确定根轨迹起点和终点。由法则3，确定根轨迹有4条渐近线ooakk135,453,2,1,0,4)12(即25.1411mjjniiazp由法则5，确定分离点。没有有限零点，故011113110141jdjdddpdii用试探法得d≈-2.3。由法则6，确定起始角和终止角。oooopk6.71)6.2690135()12(3op6.714本题无须确定终止角。由法则7，确定根轨迹与虚轴的交点。闭环特征方程为：0685234Kssss列劳斯表如下：S418KS234/5KS1(204-25K)/34S0KS356令=0，得K=8.16。根据s2行的系数构造辅助方程：05342Ks将K=8.16代人，并令s=jω代人，得ω=±1.1。继续画根轨迹。闭环极点的确定对于特定K值下的闭环极点，可用根轨迹方程的模值条件确定。①如果闭环极点较多的话，计算比较麻烦，通常先采用试探法确定实数闭环极点的数值，然后用综合除法得到其余的闭环极点。②如果某一K值下闭环系统只有一对复数极点，可直接从根轨迹图上获得闭环极点。例4-5设空间站方位控制系统开环传递函数如下，试绘制K增大时的概略根轨迹，求出使系统输出响应产生振荡的K值的取值范围，并确定K=10时系统的单位阶跃响应。)14424()20()(2ssssKsG因而当K>16.37时系统输出将会产生振荡。应用模值条件可得分离点处根轨迹增益：解由法则1-5，得根轨迹如右图所示。37.162012231dddzdpdKiid用Matlab软件直接得到K=10时系统的单位阶跃响应。4-4系统性能分析目的：在初步设计中根据已知的闭环零极点定性的分析系统性能，找出主要影响因素和次要影响因素，为系统设计提供依据。闭环系统零、极点位置对时间响应性能的影响:1)稳定性。如果闭环极点全部位于s左半平面，则系统一定是稳定的，即稳定性只与闭环极点位置有关，而与闭环零点位置无关。2)运动形式。如果闭环系统无零点，且闭环极点均为实数极点，则时间响应一定是单调的；如果闭环极点均为复数极点，则时问响应一般是振荡的。3)超调量。超调量主要取决于闭环复数主导极点的衰减率并与其他闭环零、极点接近坐标原点的程度有关。4)调节时间。调节时间主要取决于最靠近虚轴的闭环复数极点的实部绝对值；如果实数极点距虚轴最近，并且它附近没有实数零点，则调节时间主要取决于该实数极点的模值。可结合P92图3-115)实数零、极点影响。零点减小系统阻尼，使峰值时间提前，超调量增大；极点增大系统阻尼，使峰值时间滞后，超调量减小。它们的作用，随着其本身接近坐标原点的程度而加强。6)偶极子及其处理。如果零、极点之间的距离比它们本身的模值小一个数量级，则它们就构成了偶极子。远离原点的偶极子，其影响可略；接近原点的偶极子，其影响必须考虑。7)主导极点。在s平面上，最靠近虚轴而附近又无闭环零点的一些闭环极点，对系统性能影响最大，称为主导极点。凡比主导极点的实部大3～6倍以上的其他闭环零、极点，其影响均可忽略。闭环系统零、极点位置对时间响应性能的影响:根位置不同（、n不同）有不同的阶跃响应001011不等负实根1相等负实根2共轭复根3共轭虚根4正（正实部）根5根在根平面上的位置ImRe101253344122,1nns第五章线性系统的频域分析法应用频率特性研究线性系统的经典方法。时域分析法—时域数学模型—微分方程复域分析法—复域数学模型—传递函数（劳斯判据、根轨迹等）频域分析法—频域数学模型—频率特性频率特性反映了正弦信号作用下系统响应的性能。主要内容：•频率特性的基本概念和频率特性曲线绘制方法；•频域稳定判据和频域性能指标的估算。5-1频率特性1频率特性的基本概念以RC滤波网络为例：RCiuiuouiAuoA’设电容C的初始电压为uo0,取输入信号为正弦信号当uo为稳态时，记录曲线为tAuisin可见，RC网络的稳态输出仍为正弦信号。特点为：频率与输入信号的频率相同；幅值较输入信号有一定衰减；相位存在一定延迟。RCiuiuo取拉氏变换并代人初始条件得：RC滤波网络的微分方程：ioouudtduTT=RC为时间常数。][11)]0()([11)()0()()()()()()]0()([022)(UiosoiooiooioooTusATsTusUTssUTusUsUsTsUsUsUussUT代人][11)]0()([11)()0()()()()()()]0()([022)(UiosoiooiooioooTusATsTusUTssUTusUsUsTsUsUsUussUT代人][11)]0()([11)()0()()()()()()]0()([022)(UiosoiooiooioooTusATsTusUTssUTusUsUsTsUsUsUussUT代人][11)]0()([11)()0()()()()()()]0()([022)(UiosoiooiooioooTusATsTusUTssUTusUsUsTsUsUsUussUT代人再由拉氏反变换求得：)arctansin(1)1()(22220TtTAeTTAutuTtoo推导过程不要求。稳态分量：)arctansin(1)(22TtTAtuos)](sin[)(tAATTAarctan)(,11)(22式中幅值比相位差为了得到频率特性的定义，我们将其与传递函数联系起来。RC网络的传递函数为：11)(TssG取s=jω，则：)1(111111)(22221TjTTTjTjjGTj分子分母同乘)1(111111)(22221TjTTTjTjjGTj分子分母同乘)1(111111)(22221TjTTTjTjjGTj分子分母同乘将其用向量表示：TjTjeTeTTjGarctan22arctan222211111)(TjTjeTeTTjGarctan22arctan222211111)(结论：幅值比A(ω)为传递函数G(jω)的幅值。相位差φ(ω)为传递函数G(jω)的相角。)(jG)(jG)(jejG)A()(这样输出对于输入的变化可用传递函数来描述：)(jejG)A()(频率特性的定义谐波输入下，输出响应中与输入同频率的谐波分量与谐波输入的幅值之比A(ω)为幅频特性；输出响应中与输入同频率的谐波分量与谐波输入的相位之差φ(ω)为相频特性；其指数表达形式为为系统的频率特性。)(jejG)A()(频率特性的性质：与传递函数一样，频率特性也是一种数学模型。它描述了系统的内在特性，与外界因素无关。当系统结构参数给定了，则系统的频率特性也完全确定。2频率特性的几何表示法——频率特性曲线1）幅相频率特性曲线（幅相曲线或极坐标图）①对于任一给定的频率ω，频率特性值为复数，因此幅相曲线是以横轴为实轴，纵轴为虚轴的复数平面上的一条曲线。②幅频特性A(ω)为ω的偶函数，相频特性φ(ω)为ω的奇函数，因此幅相曲线(ω:0→+∞)时的部分与(ω:0→-∞)时的部分关于实轴对称。③幅相曲线中用小箭头表示ω增大时曲线的变化方向。ω=0ω=∞1/2右图为RC网络的幅相曲线2）对数频率特性曲线（伯德曲线或伯德图）包括对数幅频曲线和对数相频曲线。①对数频率特性曲线的横坐标按lgω分度，单位为弧度每秒(rad/s)。②对数幅频曲线的纵坐标按线性分度，单位为分贝(db)。③对数相频曲线的纵坐标按φ(ω)线性分度，单位为度(o)。)(lg20)(lg20)(AjGL构成半对数坐标系。例如：RC网络取T=0.5时的对数频率特性曲线。（P168图5-7）关于对数频率特性曲线的说明①横坐标按lgω分度，可实现横坐标的非线性压缩，便于在较大的频率范围内反映频率特性的变化。线性分度：当变量增大或减小1倍时，坐标间距离变化一个单位长度。对数分度：当变量增大或减小10倍（称为十倍频程）时，坐标间距离变化一个单位长度。关于对数频率特性曲线的说明)()()(321)(321)()()()()(jjjjeAAAeAjG321321)(lg20)(lg20)(lg20)(lg20)(LLLAAAAL对数幅频)()()()(321对数相频②纵坐标的分度，可将幅值的乘除运算化为加减运算，简化曲线的绘制。关于对数频率特性曲线的说明)j(Glg20)(Alg20)(L(dB)ω=0不可能在横坐标上表示出来；只标注ω的自然对数值。5-2典型环节与开环系统频率特性1典型环节1）概念根据开环零极点可将分子和分母多项式分解成因式，将因式分类，即得到典型环节。典型环节分为两大类：最小相位环节和非最小相位环节。（P169）2）用途设典型环节的频率特性为：NiisGsHsG1)()()(根据典型环节的概念，可将开环传递函数表示为N个典型环节串联的形式。)()()(ijiieAjG则开环系统的频率特性为：NiijNiieAjHjG1)]([1])([)()(则系统的开环幅频特性和开环相频特性为：NiiNiiAA11)()()()(则系统的开环对数幅频特性为：NiiNiiLAAL11)()(lg20)(lg20)(可见，了解了典型环节的频率特性，通过合成或叠加，可以简化系统开环频率特性的绘制。2典型环节的频率特性（P170图5-10和图5-11）比例环节0ImReKK)j(G频率特性：K)j(G)A(ojG)(0)(Klg20lg20)A()(L0)(K)s(G传递函数：积分环节90)(S1)s(G传递函数：j1)j(G频率特性：lg20)L(SK)s(G1传递函数：20lgK-20dB/dec-20dB/dec20dBL1(w)11jj1)j(G1)()(jGA9001arctan)()(jG惯性环节11)(TssG传递函数：11)j(TjG频率特性：2211)A(TT)(arctanT122221lg2011lg20)L(TTL()-90o+20dB/decT1微分环节)A(90)(ssG)(传递函数：j)j(G频率特性：lg20)L(120dB/dec20dB/dec-20dB振荡环节1212G(s)22222TssTssnnn传递函数：频率特性：121)G(j22TjT幅频特性：相频特性：对数幅频特性：2222)2()1(1)A(TT2212arctan)(TT)10(2222224)1(lg20)L(nnφ(ω)-180°L(ω)1/τ40lg(1/τ)-40dB/dec14dB-6dB1小123321nnn1)(ssG1j)j(G)()()(1tgjG1)()(22jGA一阶微分环节)(tg)(11lg20)(L22结论①非最小相位环节和对应的最小相位环节幅频特性相同，相频特性符号相反，幅相曲线关于实轴对称。对数幅频曲线相同，对数相频曲线关于0o线对称。例如，最小相位的惯性环节:11Ts11Ts与非最小相位的惯性环节:2211)A(TT)(arctan2211)A(TT)(arctan结论②传递函数互为倒数的典型环节对数幅频特性曲线关于零分贝线对称；对数相频特性曲线关于零度线对称。例如：惯性环节与一阶微分环节同样适用：积分环节与微分环节、振荡环节与二阶微分环节结论③振荡环节与二阶微分环节参数ωn、ζ对频率特性曲线的形状有一定影响。相频特性曲线从0o单调减至-180o。幅频特性可能有极值。onnoo90)(;180)(;0)0(时当21)(;0)(;1)0(nAAA单调减）时，，（当单调减）时，，（且单调增）时，，（且），（当)(A1)(A)(A002222rr221nr可参照结论②互为倒数的典型环节3对数幅频渐进特性曲线近似表示对数幅频曲线，可简化作图，分低频和高频两部分。以惯性环节为例，其对数幅频特性为：22221lg2011lg20)L(TTTLlg20)(01lg20)(L时，即当T11T时，即当T11T，因此T1ω，得0L(ω(令低频部分，零分贝线。高频部分，斜率为-20db/dec的直线。两条线交于处，称为惯性环节的交接频率。T1T1惯性环节的对数幅频渐进特性为：TTaTL11,lg20,0)(用渐进特性表示对数幅频特性存在误差：)()()(aLLLL()-90o+20dB/decT1-20dB/dec交接频率半对数坐标系中的直线方程：1212lglg)()(aaLLk可见，交接频率处误差最大，约-3dB。根据误差曲线可修正渐进特性曲线获得准确曲线。根据同样的分析方法，对于振荡环节，其对数幅频特性为：其对数幅频渐进特性为：nnnaL,lg40,0)(2222224)1(lg20)L(nn低频段0dB/dec线，过交接频率=n后斜率变为-40dB/dec直线。φ(ω)-180°L(ω)1/τ40lg(1/τ)-40dB/dec14dB-6dB1渐近线误差2n22n)2(])(1[lg20)(L2n2n22n)lg(20)2(])(1[lg20)(Lnn在=n处幅频特性精确曲线和近似曲线误差最大：L()=n=-20lg(2)因此，近似曲线应根据值确定修正：0.10.20.30.40.50.70.80.91L()14.07.964.441.940-2.92-4.08-5.1-64开环幅相曲线绘制绘制概略开环幅相曲线，可以反映开环频率特性的三要素：①开环幅相曲线的起点（ω=0+）和终点（ω=∞）。②开环幅相曲线与实轴的交点。③开环幅相曲线的变化范围（象限、单调性）设ω=ωx时开环幅相曲线与实轴的交点，并称ωx为穿越频率。此时：即为交点的值。的实部或的虚部)()()]()([Re)()(2,1,0;)()()(0)]()(Im[)()(xxxxxxxxxxxxxjHjGjHjGjHjGkkjHjGjHjGjHjG即为交点的值。的实部或的虚部)()()]()([Re)()(2,1,0;)()()(0)]()(Im[)()(xxxxxxxxxxxxxjHjGjHjGjHjGkkjHjGjHjGjHjG①确定起点（ω=0+）和终点（ω=∞）。例5-1某0型单位反馈系统开环传递函数为K，T1，T2均大于0，试绘制概略开环幅相曲线。)1)(1()(21sTsTKsG解：典型环节分解1111)(21sTsTKsG一个比例环节，两个惯性环节。比例环节K)A(o)(0惯性环节1)0A(o)(000)A(o)(90对任意幅值和相角都为定值。三个典型环节串联后，系统开环幅相曲线的起点：终点：K)0A(o)(000)A(o)(180根据式5-24②确定与实轴的交点。③确定变化范围。系统的开环频率特性：)1)(1(])()1[(1111)(2222212122121TTTTjTTKjTjTKjG令虚部为零：0)](Im[jG得：0x因为惯性环节从0o到-90o单调变化，故系统的开环幅相曲线从0o到-180o单调变化，故曲线在第三、四象限。jK>0ω=0ω=∞K<0KjG)](Re[①确定起点（ω=0+）和终点（ω=∞）。例5-2设系统开环传递函数为K，T1，T2均大于0，试绘制概略开环幅相曲线。)1)(1()()(21sTsTsKsHsG解：典型环节分解11111)(21sTsTsKsG一个比例环节，一个积分环节，两个惯性环节。比例环节K)A(o)(0惯性环节1)0A(o)(000)A(o)(90对任意幅值和相角都为定值。开环幅相曲线的起点：终点：)0A(o)(9000)A(o)(270积分环节)0A(o)(900)A(②确定与实轴的交点。③确定变化范围。系统的开环频率特性：)1)(1()]1()([)()(22222122121TTTTjTTKjHjG令虚部为零：0)]()(Im[jHjG得：211TTx比例5-1增加一相角恒为-90o的积分环节，故系统的开环幅相曲线从-90o到-270o单调变化，故曲线在第二、三象限。j。即曲线与实轴的交点为实部21212121,)]()(Re[TTTKTTTTKTjHjGxx2121TTTKTV=1V=2V=3结论：积分环节数每增加1，曲线绕原点旋转-90o。绘制概略开环幅相曲线的规律：①开环幅相曲线的起点取决于比例环节和积分或微分环节的个数（系统型别）。)4,3,2,1;2,1,0(4,0KK,0,0ikik设负之分）；为系统开环增益，有正处（起点为实轴上点起点为原点；的无穷远处；时起点为的无穷远处；时起点为oooikik180)90(0)90(0绘制概略开环幅相曲线的规律：②开环幅相曲线的终点取决于开环传递函数分子、分母多项式中最小相位环节和非最小相位环节的阶次和。设：m=m1+m2,m为开环传递函数分子多项式的阶次，m1为最小相位环节阶次和，m2为非最小相位环节阶次和。n=n1+n2,n为开环传递函数分母多项式的阶次，n1为最小相位环节阶次和，n2为非最小相位环节阶次和。则：018090)]()[(090)]()[()(21212121knnmmknnmmooo特殊终点：当开环系统为最小相位系统时，若：)90()(0)()(,)()(,omnjHjGmnKjHjGmn开环根轨迹增益③开环系统存在等幅振荡环节。（略）5开环对数频率特性曲线绘制①将开环传递函数进行典型环节分解，可分为三部分：②确定一、二阶环节的交接频率，标注在半对数坐标图的ω轴上。a.b.一阶环节，包括惯性环节、一阶微分环节及相应的非最小相位环节，交接频率为1/T。)0(KsKsK或c.二阶环节，包括振荡环节、二阶微分环节及相应的非最小相位环节，交接频率为ωn。v=0为比例环节，v>0为积分环节，v<0为微分环节，它们的对数幅频特性曲线均为直线，可直接取为渐进特性：NiaaiLL1)()(若记ωmin为最小交接频率，则称ω<ωmin的频率范围为低频段。5开环对数频率特性曲线绘制③绘制低频段渐进特性曲线。过点(ω0,La(ω0))在ω<ωmin范围内作斜率为-20νdB/dec的直线。显然若ω0>ωmin则该点位于低频渐进特性曲线的延长线上。直线斜率为-20νdB/dec，还需确定直线上一点：方法二：取频率为特定值ω0=1，则方法一：在ω<ωmin范围内任选一点ω0，计算00lg20lg20)(KLaKLLaalg20)1()(0方法三：La(ω0)为特殊值0，则即10K10K5开环对数频率特性曲线绘制④作ω≥ωmin频段渐进特性曲线。在ω≥ωmin频段，系统开环对数幅频渐进特性曲线为分段折线。每两个相邻的交接频率直间为直线；在每个交接频率点处斜率发生变化，变化规律取决与该交接频率对应的典型环节的类型。（P181表5-2）注意：当多个环节具有相同的交接频率时，该点处斜率变化应为各环节斜率变化值的代数和。②确定各交接频率及斜率变化值。例5-6已知系统开环传递函数为试绘制系统开环对数幅频渐进特性曲线。)40010)(1(40002000)()(22ssssssHsG解：①典型环节分解)1202120)(1()21(10)()(222ssssssHsG惯性环节：ω1=1，斜率减小20dB/dec;非最小相位一阶微分环节：ω2=2，斜率增加20dB/dec;振荡环节：ω3=20，斜率减小40dB/dec;最小交接频率：ωmin=ω1=1例5-6已知系统开环传递函数为试绘制系统开环对数幅频渐进特性曲线。)40010)(1(40002000)()(22ssssssHsG③绘制低频段渐进特性曲线。ωL(ω)dB6040200-20-400.1121020直线斜率为-20νdB/dec=-40dB/dec取ω0=1，则得直线上一点(1,20)。KLLaalg20)1()(0④绘制ω≥ωmin频段渐进特性曲线。decdBk/60,21-40dB/dec-60dB/decdecdBk/40,202-40dB/decdecdBk/80,20-80dB/dec5-3频域稳定判据奈奎斯特稳定判据（奈氏判据）反馈控制系统稳定的充分必要条件是半闭合曲线不穿过（-1，j0）点且逆时针包围临界点（-1，j0）的圈数R等于开环传递函数的正实部极点数P。GH为什么是这个点？如何计算？如何得到此曲线？1奈氏判据的数学基础1）幅角原理设有一复变量s的有理分式函数：))(())(()(2121pspszszssFReImImReFSS1ziF(S1)S1-zi映射到原点ziΓs不包围F(s)的零点，当S1沿Γs顺时针连续变化一周，(S-Zi)不积累角度Γs包围一个F(s)的零点，当S1沿Γs顺时针连续变化一周，(S-Zi)的相角积累-2π，或者说，ΓF顺时针绕F平面零点一周。如果：Γs包围一个F(s)的极点，当S1沿Γs顺时针连续变化一周，因为Pi映射到F(s)上是在无穷远，因此，ΓF逆时针绕F平面零点一周，(S-Pi)的相角积累是2π角度。Γs包围P个F(s)的极点，当S1沿Γs顺时针连续变化一周，S-Pi积累的相角为2πP，或者说，ΓF逆时针绕F平面零点P圈。结论：Γs包围P个F(s)的极点，又包围Z个F(s)的零点，当S1沿Γs顺时针连续变化一周后，ΓF顺时针绕F平面零点（Z-P）周，或：ΓF逆时针绕F平面零点（P-Z）=R周。Γs包围Z个F(s)的零点，当S1沿Γs顺时针连续变化一周，(S-Zi)的相角积累Z(-2π)，或者说，ΓF顺时针绕F平面零点Z圈。幅角原理：设s平面上的任一条闭合曲线Γs包围F(s)的Z个零点和P个极点，则s沿Γs顺时针运动一周时，在F(s)平面上闭合曲线ΓF包围原点的圈数R=P-Z。当P>Z则R>0，ΓF顺时针包围F(s)平面的原点当Pm）或（K,j0）点（n=m），K为开环根轨迹增益。),0[,js]90,0[,oojesb.若G(s)H(s)在虚轴上有极点：当有积分环节时设:ΓGH为从点G(j0+)H(j0+)起逆时针作半径∞、圆心角为的圆弧；)0(,0)(1)()(11jGsGssHsGo90当有振荡环节时设:ΓGH为从点G(jωn-)H(jωn-)起顺时针作半径∞、圆心角为的圆弧至点G(jωn+)H(jωn+)；)(,0)()(1)()(111221nnjGsGssHsGo180如：P188图5-31（a）如：P188图5-31（b）总之：故称为半闭合曲线ΓGH由开环幅相曲线和补作的半径∞的虚线圆弧组成。(5)闭合曲线ΓF包围原点的圈数R的计算（即闭合曲线ΓGH包围（-1，j0）点的圈数）这样，由幅角原理知反馈控制系统正实部极点数（F(s)的零点数）Z=P-R=P-2N，若Z=0系统闭环稳定。。负穿越的次数；正穿越的次数点左侧负实轴的次数；，穿越)(:)(:)01(:)(22NNjNNNNRGH若Z≠0系统闭环不稳定。当半闭合曲线ΓGH穿过（-1,j0）点时，表明系统闭环特征方程存在共轭纯虚根，系统可能临界稳定。例：已知单位反馈系统开环幅相曲线（K=10，P=0，V=1）如图所示，试确定系统闭环稳定时K值的范围。解：由图知开环幅相曲线与负实轴有三个交点，设交点处的穿越频率分别为ω1、ω2、ω3，设系统的开环传递函数为：j0-0.5-2-1-1.5)()(1sGsKsG已知3,2,1),(G)(G,1)(lim,1101ijjKjsGiiis且当K=10时，5.0)(G,5.1)(G,2)(G321jjj)1(3,2,1,)(G)(G1式iKjjjiii）（式2iijjGK)(1120105.01320105.1151021321KKK；；由式1和式2得：105.0)(105.1)(102)(331221111jjGjjGjjG；；若令，则：1)(G)(G1iiijjKj分别取020，对应的开环幅相曲线分别为：j0-1j0-1j0-1j0-1N+=N-=0R=2N=0Z=P-R=0系统闭环稳定N+=0，N-=1R=2N=-2Z=P-R=2系统闭环不稳定N+=1，N-=1R=2N=0Z=P-R=0系统闭环稳定N+=1，N-=2R=2N=-2Z=P-R=2系统闭环不稳定作业：5-2，5-9（2），5-12（2），5-13（1，2）补充：绘制的幅相曲线。)1s(s)3s)(2s(5)s(G2补充内容•典型环节及传递函数•基本PID控制器及调节过程典型环节及传递函数（1）比例环节)()(tKrtcKsRsCsG)()()(kR(s)C(s)比例环节微分方程：传递函数：)()(sKRsC)()()(sRsCsTsCR(s)C(s)1Ts1惯性环节（2）惯性环节（一阶系统）微分方程：传递函数：)()()(trtcdttdcT1Ts1)s(R)s(C)s(G+==tIdttrTtc0)(1)(sT1)s(GIR(s)C(s)sT1I积分环节（3）积分环节微分方程：传递函数：（4）微分环节微分方程：dttdrTtcD)()(sT)s(Gd)()(0trtcs0e)s(GR(s)C(s)sTD微分环节R(s)C(s)s0e延迟环节传递函数：传递函数：（5）延迟环节微分方程：)()()(2)(222trtcdttdcTdttcdT2nn22n22s2s1Ts2sT1)s(G（6）振荡环节（二阶系统）微分方程：传递函数：2nn22n22s2s1Ts2sT1)s(GR(s)C(s)2222nnnss基本PID控制器及调节过程控制器是根据给定值和测量值的偏差e按照预定的规律进行运算，输出调节量P对被控对象进行调节。调节器传感变送器被控对象执行器干扰-RZRS+Y断续控制：双位、三位连续控制：比例、比例积分、比例微分、比例积分微分一、比例控制1.比例控制器的特性微分方程：ekpcp传递函数：cksW)(t输入et输出kcekp传感变送器被控对象执行器干扰-RZRS+Y比例控制epPPkc比例控制的特点（1）调节及时（2）有静差（残差）浮球式水位控制器V--1ekceP2.比例带δ202122OC20mA12mA4mA（1）比例范围：控制器输出从0%~100%变化时对应的被控变量值的变化范围。（2）比例带δ：使控制器输出作100%变化时，输入信号的改变占全量程的百分数。%100maxmaxppee%100kpe对于一定的控制器，输入和输出的量程不变%100maxmaxeppe%100ckk%1001ck如果输入和输出量程相同当控制器输入和输出量程相同，比例带为比例增益的倒数。比例带举例：已知一比例温度调节器，输入量程为0~50OC，输出为0~10mA，当输入为20~30OC时，对应输出为2~8mA，求该温度调节器的比例带。解：%100maxmaxppee%100maxmaxeppe%3.3350102820303.比例带对调节过程的影响（1）δ非常大，则比例增益kc很小，比例作用很弱，系统稳定性好，但静差大。结论：δ越小，比例作用越强，系统的稳定性越差，系统的静差越小。（2）δ合适，系统输出为一衰减振荡。（3）当δ减小达到临界值δk，系统输出一等幅振荡。（4）当δ再减小，系统输出一发散振荡。施加一幅值为8的阶跃干扰信号12Kc=20Kc=50二、比例积分控制1.积分控制器特性：输出与输入的积分呈正比tt输入e输出pItIIedtTP01sTsWI1)(特点：（1）能消除静差（2）动作慢2.比例积分控制器的特性tIcedtTekP01sTksWIc11)(t输入e输出p特点：（1）能消除静差（2）动作快3.积分速度对调节过程的影响etTkekIccITtpTITI大说明积分作用弱，TI小说明积分作用强。etTekedtTekPIctIc110（1）积分时间TI：偏差e为阶跃输入信号，当积分输出增长到与比例输出相等时，所需要的时间。积分时间TI太大，积分作用太弱，当积分作用为0，输出为一比例调节。IT（2）积分时间对调节过程的影响积分时间由大到小积分时间TI合适，可得到较好的衰减振荡，并可消除静差。积分时间TI小，积分作用强，易引起系统振荡。结论：比例作用在引入积分作用的同时，消除了系统的静差，但降低了原有系统的稳定性，为了保持与原有比例作用相同的稳定性，必须适当增大比例带。10)(1sWc)511(10)(2ssWc分别取：比例P比例积分PI三、比例微分控制1.微分控制器特性：输出与输入的微分成正比dtdeTpdD微分方程：sTsWd)(传递函数：etpDtepDtt特点:（1）输出反应偏差的变化率，具有预调节作用。（2）不能消除静差，当偏差变化缓慢时，微分作用也很弱。2.比例微分控制)(dtdeTekpdc微分方程：)1()(sTksWdc传递函数：11)(skTsTksWdddc具有饱和微分环节传递函数：pttp3.微分时间对控制过程的影响dtdeTekpdc)(aTatkpdcdTt)(aTaTkpddcTd大，微分作用强，Td大小微分作用弱。（1）微分时间：输入量为斜坡函数，使比例项的输出等于微分项时所需的时间。etptTdate（2）微分时间对控制过程的影响Td大，微分作用太强，系统稳定性下降。Td合适，有预调节作用，改善调节品质Td太小，微分作用弱，Td=0，微分作用为0一般而言，比例微分控制系统随着微分时间Td的增大，其稳定性提高，但当Td超过某一值时，系统反而变的不稳定。总结：当比例作用加入微分作用，可使系统趋向稳定，为了得到与原来比例作用相同的稳定性，可适当降低比例带，从而减小静差。PPD5)(1sWc)21(10)(2ssWc分别取：四、比例积分微分控制规律微分方程：传递函数：)1(0dtdeTedtTekpdtIc)11()(sTsTksWdIc五、调节规律的选择被控对象时间常数较大，应引入微分环节。若允许有残差，可选用PD，否则选用PID。1)(TsKesGs若被控对象的传递函数为，则可根据τ/T的值来确定控制算法。被控对象时间常数较小，负荷变化不大，若允许有残差，可选用P，否则选用PI。被控对象时间常数和纯滞后较大，负荷变化较大。此时简单控制不能满足要求，应选用复杂控制。复合控制系统—前馈-反馈控制热能工程学院王桂荣蒸汽-水型热交换器进水冷凝水蒸汽出水•被控量是热水出水温度，控制量是蒸汽流量。应用实例——热交换器的控制控制器如果出水温度比期望的温度值低，就要加大蒸汽流量；如果出水温度比期望的温度值要高，就要减少蒸汽流量。TE温度控制器蒸汽流量调节阀热交换器温度变送器tg+_t干扰t反馈控制反馈控制是基于被控量的偏差进行的，没有偏差也就不存在反馈控制。反馈控制是针对系统全部干扰进行补偿，是在被控制量“变化了”的基础上的“滞后补偿”。问题：能否在干扰作用发生后，在未影响被控变量时，就开始调节？Gff(s)Gd(s)Gv(s)Gp(s)Q(s)调节阀前馈控制器T(s)++热交换器干扰通道前馈控制•原理：给系统附加一个前馈通道，利用前馈控制器所附加的控制量对被控量的补偿与干扰对被控量的影响的叠加来消除或减小干扰的影响。)(sT干扰作用下的输出：0)(sT控制目标：)()()()(sGsGsGsQpvff)()(sGsQd前馈控制前馈控制是针对系统的某种特定干扰而进行的补偿，是在被控制量“变化前”提前进行的“超前补偿”。)()()()(sGsGsGsGpvdff——前馈控制器传递函数0)()()()(sGsGsGsGdpvff干扰信号Q(s)不为零时：Gff(s)Gd(s)Gv(s)Gp(s)Q(s)调节阀前馈控制器T(s)++热交换器干扰通道前馈与反馈的比较•前馈是“开环”，反馈是“闭环”；•前馈系统中测量干扰量，反馈系统中测量被控变量；•前馈只能克服所测量的干扰，反馈则可克服所有干扰；•前馈理论上可控制到无差，反馈必因有差而控制；在工程中往往将前馈与反馈结合起来应用，构成前馈—反馈控制系统。进水出水蒸汽++前馈-反馈控制•对出水温度的变化进行反馈控制；TC反馈控制器蒸汽流量调节阀热交换器温度变送器tg+_t干扰t流量变送器+前馈控制器+FC对冷水流量的变化进行前馈补偿。前馈-反馈控制•结构图：)()()()(1)()()()()(sQsGsGsGsGsGsGsGsTpvcpvffd干扰作用下的输出：0)(sT控制目标：推导过程)()(sDsYGff(s)Gv(s)Gp(s)Q(s)调节阀前馈控制器T(s)Gd(s)++++Gc(s)_+Tg(s)反馈控制器热交换器干扰通道前馈-反馈控制)()(sDsY0)()()()(sGsGsGsGpvffd前馈—反馈控制与纯前馈控制实现“全补偿”的算式相同。)()()()(sGsGsGsGpvdff0)()()()(1)()()()()(sQsGsGsGsGsGsGsGsTpvcpvffd前馈—反馈控制系统具有下列优点从前馈控制角度，由于增添了反馈控制，降低了对前馈控制模型的精度要求，并能对未选作前馈信号的干扰加以克服。从反馈控制角度，由于前馈控制的存在，对干扰作了及时的粗调作用，大大减小了控制的负担。选用前馈－反馈控制的原则如果系统中控制通道的惯性和迟延较大，反馈控制达不到良好的控制效果，这时可引入前馈控制。如果系统中存在着经常变动、可测而不可控的扰动，反馈控制难以克服扰动对被调量的影响，这时可引入前馈控制以改善控制品质。前馈－反馈控制的其它应用锅炉汽包水位控制课后作业说明为什么引入蒸汽流量前馈信号。画出锅炉汽包水位控制的结构图，并说明其控制原理。LTFT汽包蒸汽给水省煤器热交换器的出水温度控制：负反馈控制、前馈控制、前馈—反馈控制内容小结重点：前馈控制的原理及特点前馈-反馈控制的原理及特点难点：前馈控制的原理及数学模型)()()]}()[()()({)()()(sGsGsTsGsQsGsQsGsTpvcffd)()(sDsY)()()()()()()()()()()(sGsGsGsTsGsGsGsQsGsQsTpvcpvffd)()]()()()([)()]()()(1[sQsGsGsGsGsTsGsGsGpvffdpvc返回)()()]}()[()()({)()()(sGsGsTsGsQsGsGsQsTpvcffd)()()]}()[()()({)()()(sGsGsTsGsQsGsQsGsTpvcffd)]()[()()(sTsGsGsQcff)()]([)()(sGsTsQsGcff)()()()()()()()()()()(sGsGsGsTsGsGsGsQsGsQsTpvcpvffd)()()()()()()()()()()(sGsGsGsTsGsGsGsQsGsQsTpvcpvffd)()()()()()()()()()()(sGsGsGsTsGsGsGsQsGsQsTpvcpvffd)()()()(1)()()()()(sQsGsGsGsGsGsGsGsTpvcpvffd)()(sDsYGff(s)Gv(s)Gp(s)Q(s)调节阀前馈控制器T(s)Gd(s)++++Gc(s)_+Tg(s)反馈控制器热交换器干扰通道Gff(s)Gv(s)Gp(s)Q(s)调节阀前馈控制器T(s)Gd(s)++++Gc(s)-T(s)反馈控制器热交换器干扰通道