自动控制原理课件3.2(梅晓榕)

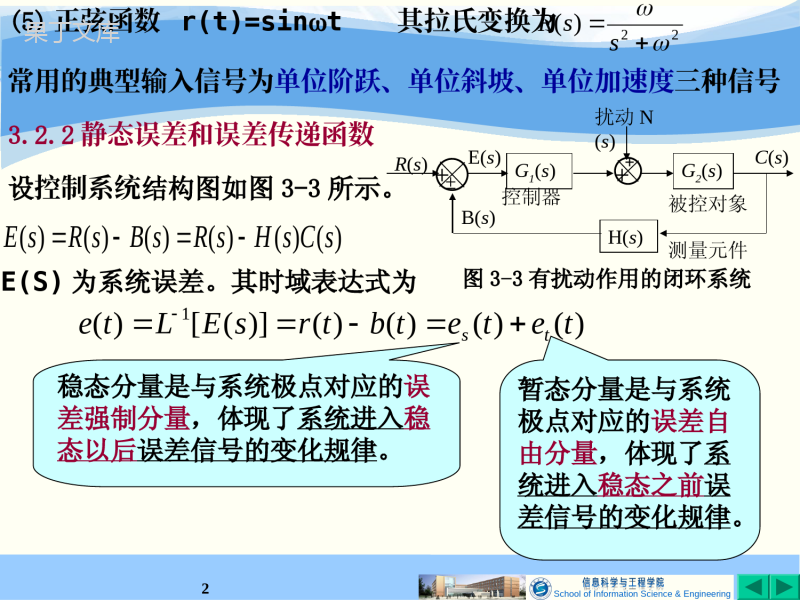
SchoolofInformationScience&Engineering13.2线性系统的静态误差控制系统的性能:动态性能和静态性能.3.2.1典型输入信号(1)单位阶跃函数其拉普拉斯变换为)0(1)0(0)(tttr21)(ssR(2)单位斜坡函数其拉普拉斯变换为ssR1)((3)单位加速度函数其拉氏变换为)0()0(0)(ttttr)0(2/)0(0)(2ttttr31)(ssR(4)单位脉冲函数其拉氏变换为R(s)=1)0()0(0)(ttt静态性能:静态误差ess.在静态条件下静态响应的期望值与实际值之间的误差.静态误差是当某特定类型的输入作用于控制系统后,达到静态时系统精度的度量.SchoolofInformationScience&Engineering2(5)正弦函数r(t)=sint其拉氏变换为常用的典型输入信号为单位阶跃、单位斜坡、单位加速度三种信号3.2.2静态误差和误差传递函数设控制系统结构图如图3-3所示。G1(s)G2(s)H(s)+R(s)C(s)扰动N(s)控制器被控对象测量元件+±E(s)+B(s)图3-3有扰动作用的闭环系统E(S)为系统误差。其时域表达式为)()()()()()(sCsHsRsBsRsE)()()()()]([)(1tetetbtrsELtets稳态分量是与系统极点对应的误差强制分量，体现了系统进入稳态以后误差信号的变化规律。暂态分量是与系统极点对应的误差自由分量，体现了系统进入稳态之前误差信号的变化规律。22)(ssRSchoolofInformationScience&Engineering3静态误差为：)(lim)(lim)(lim1sELteteettstss由输出定义稳态误差计算可利用Laplace变换终值定理)(lim)(lim0ssEteestss如果sE(s)的极点位于左半s平面(包括坐标原点)，或e(t)有极限按输入误差定义)()(limtctcertss期望值(设定值)实际值对于单位反馈系统两者等价对一般结构系统应使用输入定义SchoolofInformationScience&Engineering4)()(1)()()(1)()()(221sNsGsGsRsGsGsGsCkk(3-2)在给定和扰动同时作用下，系统输出和误差的拉氏变化分别为：ssnssrkkeesNsGsHsGsRsGsE)()(1)()()()(11)(2（3-3）给定稳态误差扰动稳态误差式中,GK(s)=G1(s)G2(s)H(s)称为系统的开环传递函数。SchoolofInformationScience&Engineering53.2.3给定作用下静态（稳态）误差计算不考虑扰动作用时，N(s)=0,由式3-3，系统误差的拉氏变换为：)()(11)()()(sRsGsRssEkE（3-4）系统误差对给定的闭环传递函数对稳定的控制系统，给定输入单独作用下的稳态误差为：)()(11lim)(lim00sRsGsssEekssssr（3-5）当输入信号形式一定时，系统的稳态误差就取决于开环传递函数描述的系统结构。SchoolofInformationScience&Engineering6)()()(')1()1()(01111sGSkpsszsksTssksGvvnjjvmiivnjjvmiik分子阶数为m,分母阶次为n的开环传递函数可表示为时间常数表达式零极点表达式K为开环比例系数或开环增益k'kv＝0称为零型系统，或有差系统；v＝1称为Ⅰ型系统，或一阶无差系统；v＝2称为Ⅱ型系统，或二阶无差系统；v〉2除复合控制外，系统难以稳定工作，不作详细讨论（3-6）v是系统开环传递函数中串联积分环节的个数也是开环传递函数所含S=0的极点的个数，称为系统的型数或无差度。SchoolofInformationScience&Engineering71.单位阶跃输入作用下的稳态误差与静态位置误差系数s)s(R1pksssrkssGse111)(11lim0定义系统静态位置误差系数)(lim0sGkkspkekkvssrp11,0时，有差系统无差系统0,1ssrpekv时，（3-7）SchoolofInformationScience&Engineering821s)s(RvksksssrkssGsGse1)(1lim)(11lim00)(lim0ssGkksv要减小稳态误差，必须增加开环总增益k或积分环节数N,这可能给动态性能或稳定带来问题，一般系统N≤2。注意：无静差系统，动态过程并不是无差2.单位斜坡输入作用下的稳态误差与静态速度误差系数（3-8）定义系统静态速度误差系数ssrvekv,00时，kekkvssrv1,1时，0,2ssrvekv时，SchoolofInformationScience&Engineering931)(ssRaksksssrksGssGse1)(1lim)(11lim2020)(lim20sGskksa要使系统在抛物线输入下不存在稳态误差，系统的型别不得低于。这时需采用复合控制。3.单位匀加速输入作用下的稳态误差与静态加速度误差系数（3-8）定义系统静态加速度误差系数ssraekv,01时，kekkvssra1,2时，0,3ssraekv时，SchoolofInformationScience&Engineering10系统类别静态误差系数典型输入下的稳态误差KpKvKa阶跃输入1斜坡输入t加速度输入t2/20型系统k00型系统k00型系统k00表3-2系统型别、稳态误差、静态误差系数和典型输入信号的关系pssrke11vssrke1assrke1pssrke11pk11vk1ak1v可提高系统无差跟踪的输入信号的阶次；K，可减小系统跟踪一定形式输入信号的定值误差.SchoolofInformationScience&Engineering11在瞬态响应保持在一个允许的范围内时,希望增加误差系数;如果在静态速度误差系数和加速度误差系数之间有任何矛盾时,主要考虑前者.如果系统输入信号是几种典型输入信号的线性组合，可利用叠加原理求出系统的总体稳态误差。例如：)(12/)(2tCtBtAtravpssrKCKBKAe1则有注意：终值定理条件:sE(s)的全部极点除坐标原点外应全部分布在S平面的左半部.例如,给定输入为正弦函数时,r(t)=sinωt其象函数为:22)(ssRSchoolofInformationScience&Engineering12221t)t(r例7系统的开环传递函数为:求输入系统的稳态误差。sksGk)(解：221t)t(r31s)s(RskssGssGssResksksss11lim)(11lim)(1)(lim20200例8系统如图:r(t)=1(t),分别求Kn=1,0.1时，系统的稳态误差。nKsssE11011)(10/s+1R(s)E(s)Y(s)+-kn解：ssR1)(nsssKssEe1011)(lim0Kn=1,ess=1/11Kn=0.1,ess=1/2SchoolofInformationScience&Engineering133.2.4外部扰动对静态（稳态）误差的影响不考虑给定作用时，R(s)=0,由式3-3，系统误差的拉氏变换为：)()(1)()()()()(2sNsGsGsHsNssEkEN（3-9）系统误差对扰动的闭环传递函数扰动单独作用于系统时，系统的输出为Cn(s)=-E(s)/H(s).即使系统响应某种形式的给定信号的稳态误差为零，其响应同一形式的扰动信号的稳态误差未必为零；同一系统对同一形式的扰动作用，由于其作用点不同，系统的稳态误差也不尽相同。即：扰动误差与输入误差不是一回事，输入无差，扰动不一定无差。SchoolofInformationScience&Engineering14例9系统如图:H(s)=1,G1(s)=K1,G2(s)=K2/s(Ts+1),求系统在单位阶跃给定和单位阶跃扰动共同作用下的稳态误差。解：系统对给定为Ⅰ型系统，可以无差响应阶跃响应，即essr=0G1(s)G2(s)H(s)+R(s)C(s)扰动N(s)控制器被控对象测量元件+E(s)+B(s)图3-3有扰动作用的闭环系统根据线性系统的叠加原理，在单位阶跃给定和单位阶跃扰动同时作用下的稳态误差为：扰动单独作用时，系统误差的拉氏变化为：系统结构稳定，且满足终值定理的使用条件，扰动单独作用时稳态误差为：sKKsTsKsNTssKKTssKsEn1)()1(1)1()(212221210/1)(limKssEensssn1/1KeeessnssrssSchoolofInformationScience&Engineering15Gc(s)Gp(s)H(s)R(s)N(s)Y(s)++--解：)(1)(tAtnsAsN)()()(1)()(lim)(lim00sNsGsHsGsssEekpsnsssn例10系统如图:n(t)=A1(t),分析系统的扰动误差。sAsGsHsGskps)(1)()(lim0)0()0(1)0()0()0(1)0()0(ckcKkpGAGGAGAGHGGk(0)≥1SchoolofInformationScience&Engineering16G(s)R(s)E(s)C(s)++-+Gd(s)图3-4按给定补偿的复合控制系统3.2.5提高系统控制精度的措施增加前向通道积分环节的个数或增大系统的开环比例系数，可以减小系统的给定误差；增加E(s)到扰动作用点之间的积分环节个数或放大倍数，可以减小系统的扰动误差；例11系统如图:G(s)=1/(s3+2s2+3s+4).试确定补偿通道的传递函数，使系统在单位斜坡给定作用下无稳态误差。通常在系统中引入与给定作用有关或与扰动作用有关的附加控制作用，构成复合控制系统。SchoolofInformationScience&Engineering17解：系统误差的拉氏变化为：223231532)(432)()(1)()(1)()()(sssssGssssRsGsGsGsCsRsEdd如果：432)(1)(23ssssGsGd可以实现对任一给定的全补偿。该补偿环节为三阶微分调节器，不宜实现且易引入高频干扰。根据具体的输入形式，实现近似补偿。sE(s)满足拉氏变换终值定理的条件，要使系统在单位斜坡给定作用下无稳态误差，应有0)(lim0ssEesssr（3-10）根据系统误差拉氏变化表达式（3-10），使补偿通道传递函数43)(ssGd即可实现斜坡给定无稳态误差。比例微分调节器