自动控制原理课件3.3(梅晓榕)

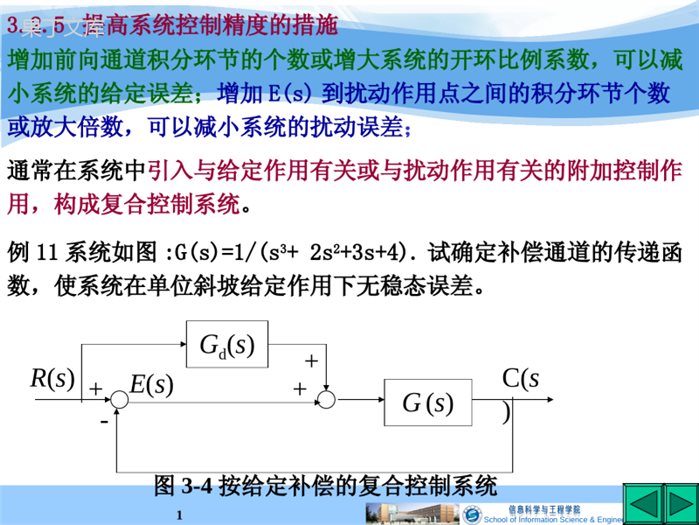
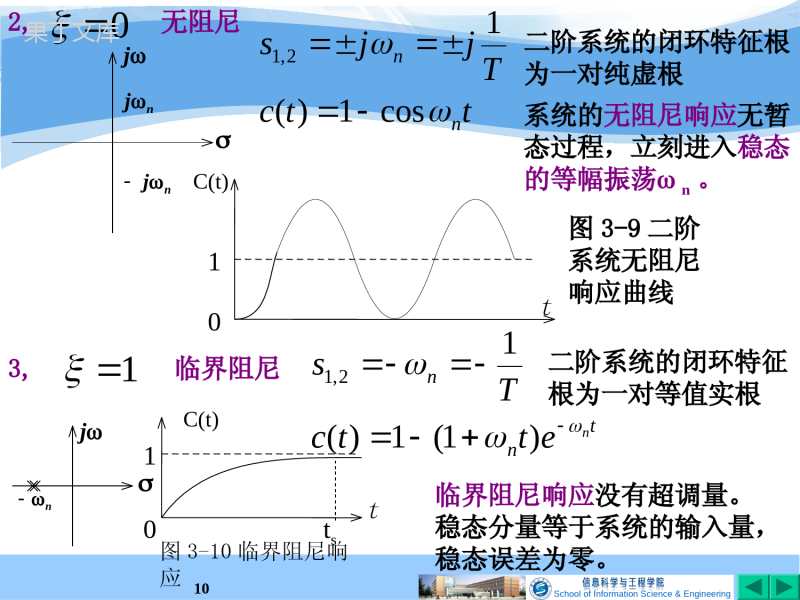
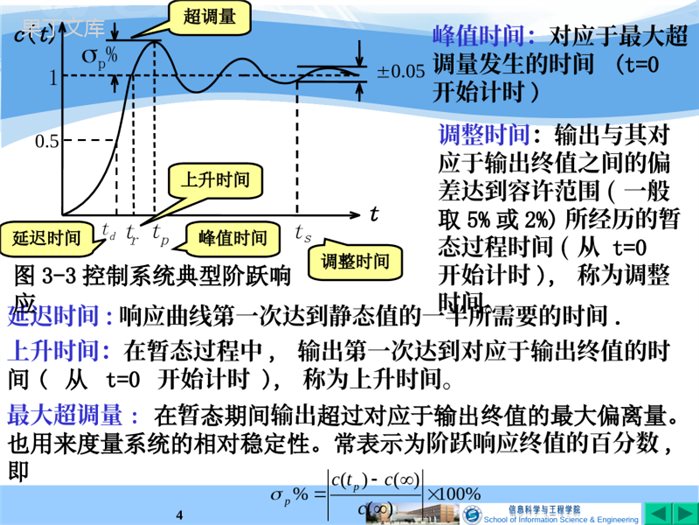
SchoolofInformationScience&Engineering1G(s)R(s)E(s)C(s)++-+Gd(s)图3-4按给定补偿的复合控制系统3.2.5提高系统控制精度的措施增加前向通道积分环节的个数或增大系统的开环比例系数，可以减小系统的给定误差；增加E(s)到扰动作用点之间的积分环节个数或放大倍数，可以减小系统的扰动误差；例11系统如图:G(s)=1/(s3+2s2+3s+4).试确定补偿通道的传递函数，使系统在单位斜坡给定作用下无稳态误差。通常在系统中引入与给定作用有关或与扰动作用有关的附加控制作用，构成复合控制系统。SchoolofInformationScience&Engineering2解：系统误差的拉氏变化为：223231532)(432)()(1)()(1)()()(sssssGssssRsGsGsGsCsRsEdd如果：432)(1)(23ssssGsGd可以实现对任一给定的全补偿。该补偿环节为三阶微分调节器，不宜实现且易引入高频干扰。根据具体的输入形式，实现近似补偿。sE(s)满足拉氏变换终值定理的条件，要使系统在单位斜坡给定作用下无稳态误差，应有0)(lim0ssEesssr（3-10）根据系统误差拉氏变化表达式（3-10），使补偿通道传递函数43)(ssGd即可实现斜坡给定无稳态误差。比例微分调节器SchoolofInformationScience&Engineering33.3线性系统暂态响应稳定性:系统在扰动作用后能否建立新的平衡状态。静态误差:系统静态精度.暂态响应过程：系统由接受外作用开始到新平衡状态出现的中间过渡过程.也称动态响应。暂态响应性能指标：以系统在单位阶跃输入作用下的衰减振荡过程(或称欠阻尼振荡过程)为标准来定义的.动态品质指标：比较重要的是最大超调量和调整时间。响应的平稳性系统响应的初始快速性研究动态响应的方法(1)数值解(2)高价近似一二阶。系统响应的总体快速性典型性能指标：最大超调量、上升时间、延迟时间、峰值时间和调整时间。SchoolofInformationScience&Engineering4延迟时间:响应曲线第一次达到静态值的一半所需要的时间.最大超调量:在暂态期间输出超过对应于输出终值的最大偏离量。也用来度量系统的相对稳定性。常表示为阶跃响应终值的百分数,即峰值时间：对应于最大超调量发生的时间(t=0开始计时)调整时间：输出与其对应于输出终值之间的偏差达到容许范围(一般取5%或2%)所经历的暂态过程时间(从t=0开始计时),称为调整时间。上升时间：在暂态过程中,输出第一次达到对应于输出终值的时间(从t=0开始计时),称为上升时间。0.05图3-3控制系统典型阶跃响应%100)()()(%cctcpp超调量c(t)t1p%trtpts上升时间峰值时间调整时间0.5td延迟时间SchoolofInformationScience&Engineering53.4一阶系统的暂态响应11TsC(s)R(s)R(s)C(s)+-Ts1图3-5一阶系统方框图3.4.1一阶系统的单位阶跃响应ssRttr1)(),(1)()1(1)(TsssC由拉氏反变换得单位阶跃响应C(t)为：)0(1)(/tetCTt632.01)(,1)(,0)0(1eTccc系统的时间常数T:阶跃响应曲线c(t)达到其终值的63.2%的时间.当经过的时间t=3T,4T时,响应将分别达到静态值的95%或98%.2%C(t)t1ts=4T0.632TSchoolofInformationScience&Engineering63.4.2一阶系统的单位脉冲响应1)(),()(sRttr单位脉冲输入有11)(TssC系统单位脉冲响应为：TteTtC/1)(01/TtC(t)图3-6一阶系统单位脉冲响应3.4.3线性定常系统的重要特性一个输入信号导数的时域响应等于该输入信号时域响应的导数。一个输入信号积分的时域响应等于该输入信号时域响应的积分。3.5二阶系统的暂态响应在分析或设计系统时，二阶系统的响应特性常被视为一种基准。TCtC1)0()(maxSchoolofInformationScience&Engineering7nT时间常数阻尼比无阻尼自然振荡角频率121))((2)(22212222TssTsssssGnnnn)s(snn22R(s)C(s)+-R(s)C(s)+-1TsKs1系统传递函数为：KsTsKsRsCsG2)()()(（3-11）令：KTTKn2123.5.1典型二阶系统方框图n2R(s)C(s)s2sn2+n2R(s)C(s)12122TssTSchoolofInformationScience&Engineering81,10欠阻尼dnnjs122,121ndn3.5.2二阶系统的闭环极点二阶系统的闭环特征方程：122,1nns0222nnss闭环特征根为一对具有负实部的共轭复根，位于s平面的左半平面。二阶系统的闭环特征根自然振荡频率jdjn0s平面s1s2n图3-7欠阻尼系统特征根在s平面的分布cosSchoolofInformationScience&Engineering9单位阶跃响应：sjsjsssssCdndnnnnn1))((12)(2222)sin(111)(2tetcdtnC(t)t01图3-8欠阻尼阶跃响应曲线（3-12）SchoolofInformationScience&Engineering102,无阻尼0ttcTjjsnncos1)(12,1jnjnj3,临界阻尼1tnnnettcTs)1(1)(12,1jn临界阻尼响应没有超调量。稳态分量等于系统的输入量，稳态误差为零。二阶系统的闭环特征根为一对纯虚根C(t)t10图3-9二阶系统无阻尼响应曲线二阶系统的闭环特征根为一对等值实根系统的无阻尼响应无暂态过程，立刻进入稳态的等幅振荡n。tC(t)01ts图3-10临界阻尼响应SchoolofInformationScience&Engineering114,过阻尼1122,1nnsjs1s2闭环特征根为一对不等值的负实根tC(t)01ts图3-11过阻尼响应1/1/11)(21/12/212121TTeTTeekektcTtTttsts响应的曲线与临界阻尼时一样，按指数规律单调增加，但调节速度更慢。若两个特征根相差3倍以上，可把过阻尼二阶系统简化为一阶系统近似分析。系统响应的暂态分量为两个衰减的指数项，相应的稳态分量为1。5,不稳定响应0二阶系统的闭环特征根位于s平面的右半部，系统的响应是发散的，此时系统不能工作。SchoolofInformationScience&Engineering12从以上分析可以看出：1）<0时，响应是发散的，系统不能正常工作；2）1时，响应与一阶系统相似，没有超调，但调节速度慢；3）=0时，系统以最快的速度进入稳态，但响应曲线是等幅振荡；4）1>>0时，虽然响应有超调，但上升速度较快，调节时间也较短。合理选择的取值，使系统具有满意的响应快速性和平稳性。工程上有时把阻尼比=0.707的二阶系统称为二阶最优系统。控制系统设计以欠阻尼为主，以下分析针对欠阻尼3.5.3二阶系统暂态响应的性能指标)sin(111)(2tetcdtn（3-12）上升时间：令c(t)=1,代入（3-12）式dnrt)1(tan11212（3-13）SchoolofInformationScience&Engineering13峰值时间：阶跃输入作用于系统开始，响应达到第一个峰值的时间dnpt21（3-14）0)(pttdttdc（3-15）最大超调量：发生在t=tp,c()=1,)1/(21)(eetcpntpp（3-17）调整时间：)()()()(sttcctc则：)()sin(112sdtttten即：)(112stttenSchoolofInformationScience&Engineering14211ln1nst（3-18）工程上当0.1<<0.9时，用下列二式计算调整时间。)(%244ctns)(%533ctns（3-19）（3-20）阻尼系数与超调量p%和调整时间ts的关系1)阻尼系数p%ts在0.707处有一个最小值2)ntsp%(保持不变)SchoolofInformationScience&Engineering15例12：一个二阶系统，要求求系统极点位置。5.0707.0st＝jn450288885.0445707.0222,10nnnsjst＝＝＝dnnjs122,1SchoolofInformationScience&Engineering16例13：在图3-12系统中=0.6，n=5rad/s,当系统受到阶跃输入信号作用时，试求上升时间、峰值时间、最大超调量和调整时间。)s(snn22R(s)C(s)+-图3-12二阶系统E(s)解：根据给定的和n的值，可求得3412nnd1）上升时间tr：)(55.0493.014.3stdr)(93.034tantan11弧度d2）峰值时间tp：3）最大超调量：4）调整时间ts：)(785.0414.312stdnp095.014.3)4/3()1/(2eep)(%2)(33.13444cstns)(%5)(1333cstsSchoolofInformationScience&Engineering17控制系统三个基本性能要求：1）稳定性确定系统是否稳定：稳定性定义、稳定的充要条件、劳斯判据.2）准确性使系统误差尽可能小：静态误差的概念及计算方法、终值定理条件.3）快速性亦即系统动态要求：要求系统超调量小，调节时间短。掌握一阶、二阶系统的数学模型及典型响应特点，能熟练确定一阶、二阶系统特征参数，掌握其欠阻尼系统动态特性的计算方法及条件，掌握典型欠阻尼二阶系统参数、极点位置与动态性能的关系。3.6小结SchoolofInformationScience&Engineering18作业题1.已知单位反馈的开环传递函数为：式中T1=0.1(s),T2=0.5(s)，输入信号r(t)=2+0.5t求：1）K=1时的系统稳态误差，2）是否可选择一合适的K值使系统的稳态误差为0.025?)1)(1(10)(21sTsTsKsG2.下图所示系统单位阶跃响应曲线为b图。试确定系统参数和k1、k2、a.R(s)C(s)+-)(2assk1kC(t)t30.10(b)4