热工过程自动控制-课件--自动控制原理部分总结

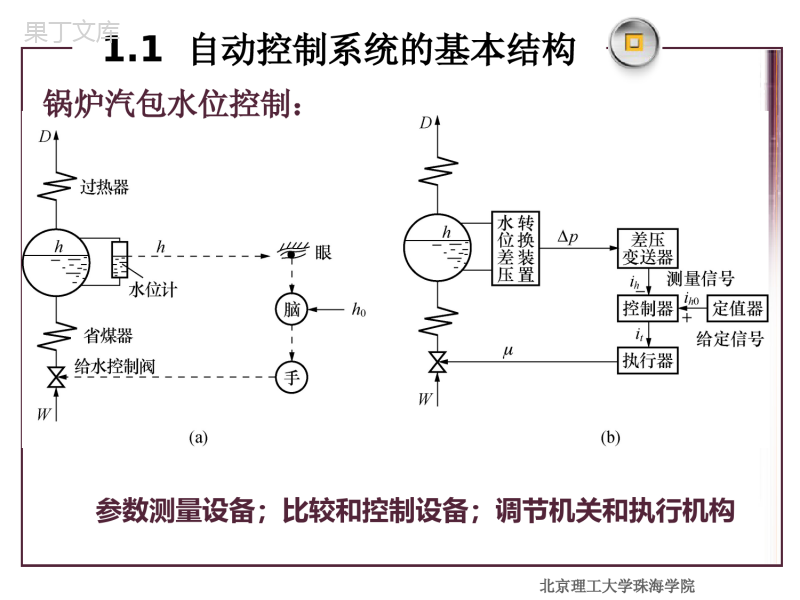
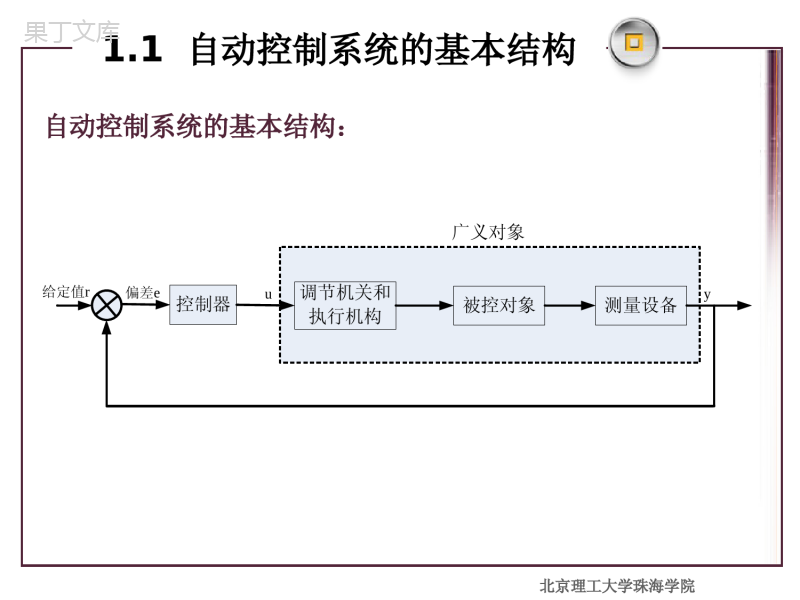
热工过程自动控制系统北京理工大学珠海学院锅炉汽包水位控制：1.1自动控制系统的基本结构参数测量设备；比较和控制设备；调节机关和执行机构北京理工大学珠海学院自动控制系统的基本结构：控制器调节机关和执行机构被控对象测量设备给定值r偏差euy广义对象1.1自动控制系统的基本结构北京理工大学珠海学院(1)被控量：表征生产过程是否正常而需要控制的物理量。(2)扰动：引起被控量偏离其给定值的各种原因。(3)对象的输入和输出：被控对象的生产过程．以所有扰动作为输入，以被调量作为输出。(4)调节量：通过调节器来改变某一个量，使被调量回到期望值。(5)给定值：根据生产工艺要求，被控量应该达到的数值。(6)偏差：期望值和实际被调量之间的差值。1.2自动控制系统的基本参数北京理工大学珠海学院稳态工况平衡状态：运动中的自动调节系统，其输入信号和输出信号都不随时间变化时。系统的静态特性：在系统处于平衡状态时，输出信号和引起它变化的输入信号之间的关系。静态特性的描述：1）描述系统各变量之间关系的数学方程为代数方程；2）在输入、输出为直角坐标图上，用曲线来表示。系统的静态特性表达式可以是线性方程或非线性方程。不是所有的环节都有静态特性，比如：积分环节1.3控制系统的静态特征和动态特征系统的动态特性系统的静止状态被破坏，系统中各变量随时间发生变化，微分方程是表征系统动态特性的一种最基本的数学方程,它不仅包含变量本身,也包含这些变量的导数.在自动化工作中，了解系统的静态是必要的，但是了解系统的动态更为重要。因为在生产过程中，干扰是客观存在的，是不可避免的，就需要通过自动化装置不断地施加控制作用去对抗或抵消干扰作用的影响，从而使被控变量保持在工艺生产所要求控制的技术指标上。北京理工大学珠海学院1.按给定值的形式分类(1)定值控制系统:给定值为常数例如:汽包锅炉给水自动调节系统中的主蒸汽温度(2)程序控制系统:给定值按预定规律变化给定值是时间的函数,需要有专门程序发送装置例如:金属热处理的炉温自动调节系统(3)随动控制系统:给定值随机变化其数值决定于一些外来因素的变化例如:锅炉燃烧过程自动调节时,负荷决定燃料,燃料决定空气量,负荷的变化是不能预订的1.4控制系统的分类北京理工大学珠海学院(1)闭环控制系统:信号沿箭头方向形成一个闭环,主要标志是反馈,因此也称反馈系统.主要特点:a)它是基于偏差的控制，因此，只有当偏差存在时，才会产生控制作用．b)各种扰动，系统都会产生控制作用．c)在调节结束时，可使被控量等于或接近给定值．d)调节的速度相对缓慢．1.4控制系统的分类2.按调节系统的工作方式分类北京理工大学珠海学院(2)开环控制系统:调节系统中不存在反馈回路，调节器只是根据直接或间接反映扰动的输入信号进行调节．工作原理：调节器接受了被调对象受到的扰动信号，按预定的调节规律立即对被调对象产生一个调节作用，以抵消扰动信号对被调量的影响．特点：a)由于扰动影响被控量的同时，调节器的调节作用已产生，所以调节速度相对比较快.b)由于没有被控量的反馈，所以调节结束时不能保证被控量等于给定值．1.4控制系统的分类北京理工大学珠海学院闭环系统VS开环系统1.4控制系统的分类基于反馈调节缓慢调节精确基于扰动调节快速调节粗略北京理工大学珠海学院(3)前馈－反馈系统:在扰动发生时,反馈还没有发生时,先由前馈部分依据扰动信号进行粗调,尽快使调节作用一开始就能大致抵消扰动的作用的影响,而被控量和给定值出现的一些偏差,则可以由反馈部分进行细调.较快的调节速度较高的调节质量1.4控制系统的分类北京理工大学珠海学院1.评价系统质量的主要特征:稳定,快速,准确(1)稳定性1.5控制系统的质量评定非周期衰减过程衰减震荡过程等幅震荡过程发散震荡过程X√√？临界稳定状态北京理工大学珠海学院1.5控制系统的质量评定(1)稳定性判断的指标:1)衰减率:每经过一个波动周期,被调量波动幅度减少的百分数Y1,y3分别是偏离稳定态值的第一,第三个波峰幅值该值还可以表征系统稳定裕量,一般取0.75~0.9.131-yyy.,0;,10系统是不稳定的时系统是稳定的时北京理工大学珠海学院1.5控制系统的质量评定(2)准确性1）动态偏差是指整个调节过程中被调量偏离给定值的最大偏差值.2）静态偏差e∞是指调节过程结束后,被调量与给定值之间的偏差.(3)快速性调节时间ts:从被控量受到扰动,过程开始变化直到结束所需要的时间.±5%or±2%北京理工大学珠海学院本章小结1）.自动控制的基本结构控制器调节机关和执行机构被控对象测量设备给定值r偏差euy广义对象2）.自动控制的基本参数被调量扰动对象的输入输出调节量给定值偏差3）.控制系统的特性静态动态北京理工大学珠海学院本章小结4）.控制系统的分类按定值的形式分：定值、程序、随动按工作方式分：闭环、开环、前馈-反馈5）.控制系统的质量评定稳定性衰减率准确性动态偏差静态偏差快速性调节时间积分指标自动控制系统的数学描述2拉氏变换微分方程传递函数CH2自动控制系统的数学描述CH2自动控制系统的数学描述2.1拉普拉斯变换2.1.1拉式变换的定义复平面内实函数x(t)的拉氏变换1-,,,s,s(s).,s,][][,x(t)e(s)](t)[0st-jjXLdtXxL为实变量为复变量记为的函数变换结果是中的实函数求拉氏变换表示对式中变量：实数变为复数函数：原函数变为象函数拉氏反变换:已知x(t)的拉氏变换X(s)求x(t),通常用表示,计算式为:][1L叫做像函数叫做原函数其中X(s),(t),)(21)]([L(t)-1-xdsesXjsXxjjst是一一对应的和X(s)0)(t)(txCH2自动控制系统的数学描述拉氏变换存在的条件:dtx0t-(t)e,(2);(1)x(t)使存在一个实数分段连续2.1.2拉氏变换的主要性质①线性定理②延迟定理③复平移定理④时标变换定理(s))(](t)bx(t)[2121bXsaXaxLCH2自动控制系统的数学描述)(])-(t[-sXexLsa)(s](t)[-XxeLat)(])at([asaXxLCH2自动控制系统的数学描述⑤微分定理如果是在零初始条件下，则)()]([sXstxLnnn阶导数的拉氏变换热工过程经常讨论的是在零初始条件下的情况2.1.2拉氏变换的主要性质⑥积分定理0t]x(t)dt[1)(1](t)dt[ssXsxLCH2自动控制系统的数学描述)0(1)0(1)(1])([)2()1(222xsxssXsdttxL一重积分的拉氏变换二重积分的拉氏变换零初始条件下的，n重积分的拉氏变换)(1])([sXsdttxLnn⒈⒈方波函数：方波函数：tAtttr0,0,0)(和1)(tt0)()(0tt时，当当当A=1A=1时，记为。时，记为。)(t常见的几种输入函数常见的几种输入函数CH2自动控制系统的数学描述理想单位脉冲函数：理想单位脉冲函数：。即积分面积为，且定义：11)(000)(dtttttt0)(t拉氏变换：拉氏变换：1)]([tLCH2自动控制系统的数学描述在实际中，如果系统的脉动输入量值很大，在实际中，如果系统的脉动输入量值很大，而持续时间与系统的时间常数相比非常小时，可而持续时间与系统的时间常数相比非常小时，可以用脉冲函数去近似表示这种脉动输入。以用脉冲函数去近似表示这种脉动输入。如脉冲如脉冲电压信号、冲击力、阵风等。电压信号、冲击力、阵风等。理想的脉冲函数在现实中是不存在的，它理想的脉冲函数在现实中是不存在的，它只有数学上的意义。只有数学上的意义。当描述脉冲输入时，脉冲的面积或者大小是当描述脉冲输入时，脉冲的面积或者大小是非常重要的，而脉冲的精确形状通常并不重要。非常重要的，而脉冲的精确形状通常并不重要。CH2自动控制系统的数学描述⒉⒉阶跃函数：阶跃函数：0,0,0)(tAttrAA为阶跃幅度为阶跃幅度拉氏变换：拉氏变换：sAtrL)]([A=1A=1时称为单位阶跃函数，记为时称为单位阶跃函数，记为1(t)1(t)。。stL1)](1[A00ttr(r(tt))1100tt1(1(tt))CH2自动控制系统的数学描述如指令的突然转换，电源的突然接通，如指令的突然转换，电源的突然接通，负载的突变等，都可视为阶跃作用。负载的突变等，都可视为阶跃作用。发生在发生在t=0t=0时的阶跃函数，相当于在时的阶跃函数，相当于在时间时间t=0t=0时，把一个定常信号突然加到系时，把一个定常信号突然加到系统上。统上。CH2自动控制系统的数学描述⒊⒊斜坡函数斜坡函数0,0,0)(tAtttrA=1A=1时称为单位斜坡函数。时称为单位斜坡函数。拉氏变换：拉氏变换：2][sAAtL21][stL1t0Ax(x(tt))斜坡函数的一阶导数为常量斜坡函数的一阶导数为常量AA，这种函数，这种函数表示由零值开始随时间表示由零值开始随时间tt作线性增长（恒速增作线性增长（恒速增长）的信号，故斜坡函数又称为长）的信号，故斜坡函数又称为等速度函数等速度函数。。CH2自动控制系统的数学描述[[提示提示]]：上述几种典型输入信号的关系如下：：上述几种典型输入信号的关系如下：][)](1[)(22AtdtdtAdtdtA上述几种典型响应有如下关系：上述几种典型响应有如下关系：单位脉冲单位脉冲函数响应函数响应单位阶跃单位阶跃函数响应函数响应单位斜坡单位斜坡函数响应函数响应积分积分积分积分CH2自动控制系统的数学描述44正弦函数正弦函数tASintr)(为角频率。为振幅，A拉氏变换：拉氏变换：22]sin[sAtAL用正弦函数作输入信号，可以求得系统对用正弦函数作输入信号，可以求得系统对不同频率的正弦输入函数的稳态响应，由此分不同频率的正弦输入函数的稳态响应，由此分析系统的性能。析系统的性能。（频域分析）（频域分析）CH2自动控制系统的数学描述2.1.4拉氏反变换利用拉普拉斯变换对照表,由象函数X(s)求出原函数x(t).象函数X(s)为s的有理分式时,必须将复杂的拉普拉斯函数式X(s)分解成若干个简单函数之和.CH2自动控制系统的数学描述)()()()())(()()s()s()s(2121nnsssssssssssssBABX主要任务：求，求出可以通过查表得到其原函数2.1.4拉氏反变换1)当X(s)具有单实极点时（各个根互不相同）)(A)(A)(A)())(()()s()s()s(n221121nnsssssssssssssBABXCH2自动控制系统的数学描述isssXA)s)(s(iiCH2自动控制系统的数学描述2.2系统的动态特性稳态时,该关系为系统的稳定特性,是一个代数函数.动态时,该关系为系统的动态特性,是一个微分方程.系统输入：x输出：y？y=f（x）物理模型数学模型CH2自动控制系统的数学描述2.2系统的动态特性-微分方程vs传递函数2.2.1数学模型的建立)(tur)(tucCRi已知：如右图所示的RC电路，已知电阻阻值为R，电容为C.当输入信号为ur（t），输出信号为uc（t）时，试写出系统的动态特性方程。1）写出输入电压和输出电压的差值变化引起的关系式，根据欧姆定律有：2）设电容两端的初始电压为零，输出信号与i的关系式为：3）消去中间变量得到）（1-2)()(RtutuicridtCtutc01)()()()()()()())()(()()()(1)(00tutudttduRCtutudttduRCdttutuRCtudtRtutuCturcccrctcrctcrc整理得两边求导CH2自动控制系统的数学描述RC电路的动态方程式静态特性建立系统微分方程的步骤：Step1：分析系统的工作原理、结构组成，找出相关变量，确定系统的输入量和输出量；Step2：建立相关变量的函数关系；Step3：消去中间变量，得到仅含输入和输出的微分方程；Step4：将方程整理写成规范形式，输出量放在左边，输入量放在右边，导数的阶次按照降序，从左到右排列。CH2自动控制系统的数学描述CH2自动控制系统的数学描述2.2.1数学模型线性定常系统的微分方程xbdtxdbdtxdbdtxdbyadtydadtydadtydammmmnnnnmmnn0110111111CH2自动控制系统的数学描述2.2.2传递函数定义：在零初始条件下：系统的输出的拉氏变换和输入的拉氏变换之比。零初始条件：研究对象是系统受到扰动后，系统的变化情况，研究的起点就在系统发生变化的那一刻。0-00+系统没有输入和输出系统处于平衡状态输入函数r(t)及其各阶导数均为零输出函数c(t)及其各阶导数均为零系统输入在此刻发生变化，输出也变化系统的平衡状态在此刻被打破CH2自动控制系统的数学描述)()]([sXstxLnn2.2.2传递函数xbdtxdbdtxdbdtxdbyadtydadtydadtydammmmnnnnmmnn0110111111对微分方程的两边分别做拉氏变换)()()()()()()()(01110111sXbssXbsXsbsXsbsYassYasYsasYsammmmnnnn线性定理))(())((01110111bsbsbsbsXasasasasYmmmmnnnn01110111)()(asasasabsbsbsbsXsYnnnnmmmmCH2自动控制系统的数学描述01110111)()()s(asasasabsbsbsbsXsYGnnnnmmmmA（s）为系统的特征方程A（s）的根为传递函数的极点B（s）=0的根为传递函数的零点CH2自动控制系统的数学描述2.2.2传递函数)(tur)(tucCRi求下图所示RC电路以ur(t)为输入，uc(t)为输出时的传递函数。)()()(tutudttduRCrcc)(turG(s))(tuc11)()()()()()(RCssUsUsGsUsUsRCsUrcrccRC电路的传递函数CH2自动控制系统的数学描述2.2.2传递函数传递函数的物理意义，表示了系统的动态特性，是系统在复频域的数学模型。特点：1）只适用于线性定常系统；2）只能表示一个输入对一个输出的关系；3）表示系统或环节的固有特性，和输入信号的具体形式、大小无关；便于对同一系统，有不同输入信号时的分析2.2.3输入响应法1）脉冲响应CH2自动控制系统的数学描述当输入信号r(t)为单位脉冲函数δ(t)时，输出信号c(t)叫做系统的脉冲响应。2）阶跃响应当输入信号r(t)为单位阶跃函数1(t)时，输出信号c(t)叫做系统的单位阶跃响应。xy1yG1(s)G2(s)CH2自动控制系统的数学描述2.3环节的连接方式和典型环节的动态特性2.3.1环节的基本连接方式：串联、并联、反馈。1．串联两个环节串联后总的传递函数为：)()()()()()()()()(2111sGsGsYsYsXsYsXsYsG)()()(11sXsYsG)()()(12sYsYsG判断标准：前一个环节的输出，是后一个环节的输入2．并联y1G1(s)xy2G2(s)++y)()()()()()()()()()()()(212121sGsGsXsYsXsYsXsYsYsXsYsGCH2自动控制系统的数学描述CH2自动控制系统的数学描述G1(s)xG2(s)eb+-y)()()(1sEsYsG)()()(21sGsGsGk3．反馈(1)负反馈联接G1(s)为前向传递函数G2(s)为反馈通道传递函数)()()(2sYsBsGGk(s)为开环传递函数)(1)()()(1)()()()(1211sGsGsGsGsGsXsYsGkG1(s)xG2(s)yeb++)(-1)()()(-1)()()()(1211sGsGsGsGsGsXsYsGk(2)正反馈联接CH2自动控制系统的数学描述CH2自动控制系统的数学描述2.4物理函数传递函数的推导2.4.1系统的方框图表示(1)能直观地表达自动控制系统中各设备之间相互作用与信号传递关系的示意图称为自动控制系统的方框图。(2)方框图的四个要素①信号线：用箭头表示信号“x”的传递方向的连接线。②汇交点(相加点、综合点)：表示两个信号“x1”与“x2”的代数和。③分支点(引出点)：表示把信号“x”分两路取出。④环节：方框图中的一个方框。方框图的四个要素：CH2自动控制系统的数学描述系统分析3时域分析法分析一阶系统和二阶系统劳斯变换CH3系统分析什么是时域分析法？CH3系统分析根据系统的根据系统的微分方程微分方程，求出当，求出当输入为某种输入为某种时间函数时时间函数时，微分方程式的解，即，微分方程式的解，即调节系统的调节系统的时间响应时间响应，从而进一步分析，从而进一步分析系统的稳定性系统的稳定性及其及其稳态和动态品质稳态和动态品质。。稳定性能快速性能准确性能微分方程CH3系统分析描述系统动态时，系统的输入量和输出量描述系统动态时，系统的输入量和输出量之间的关系的方程，因为在动态时，之间的关系的方程，因为在动态时，xx、、yy都随时间而变化，所以它是一个微分方程。都随时间而变化，所以它是一个微分方程。线性定常系统xbdtxdbdtxdbdtxdbyadtydadtydadtydammmmnnnnmmnn0110111111分析热工过程自动调节系统时，常假定分析热工过程自动调节系统时，常假定输入信号为输入信号为阶跃函数阶跃函数热工过程的输入扰动经常是热工过程的输入扰动经常是有限量的变有限量的变化化，如果在，如果在阶跃式有限变化量阶跃式有限变化量的扰动下调节的扰动下调节系统的工作能满足生产上的要求，那么当扰系统的工作能满足生产上的要求，那么当扰动为动为缓慢的有限变化量缓慢的有限变化量时，系统必然也能满时，系统必然也能满足生产上的要求。足生产上的要求。CH3系统分析什么是时域分析法？CH3系统分析根据系统的根据系统的微分方程微分方程，求出当，求出当输入为某种输入为某种时间函数时时间函数时，微分方程式的解，即，微分方程式的解，即调节系统的调节系统的时间响应时间响应，从而进一步分析，从而进一步分析系统的稳定性系统的稳定性及其及其稳态和动态品质稳态和动态品质。。调节系统的时间响应调节系统的时间响应)()()()(001222trbtcadttdcadttcda•某调节系统的微分方程令输入信号r(t)为单位阶跃函数，即r(t)=1(t))(1)()()(001222tbtcadttdcadttcda•线性方程•非齐次方程这个方程的解c(t)就是在输入信号为单位阶跃函数时，调节系统的时间响应CH3系统分析时域分析以线性定常微分方程的时域分析以线性定常微分方程的解解来分析系统的来分析系统的性能。性能。线性常微分方程的解线性常微分方程的解==齐次方程的通解齐次方程的通解++非齐次方程的一个特解非齐次方程的一个特解齐次方程的齐次方程的通解通解，只与微分方程（系统本身，只与微分方程（系统本身的特性或系统的特征方程的根）有关，与输入信的特性或系统的特征方程的根）有关，与输入信号无关，称为系统的号无关，称为系统的瞬态响应瞬态响应。。特解特解与微分方程和输入有关。一般来说，当时与微分方程和输入有关。一般来说，当时间趋于无穷大时特解趋于一个间趋于无穷大时特解趋于一个稳态的数稳态的数，称为，称为系统系统的稳态响应的稳态响应。。CH3系统分析稳态过程（平衡过程，静态过程）：表征系统输出最终跟踪输入的程度，提供系统稳态误差的信息，反映系统稳态性能。y(t)t动态过程动态过程扰动稳态过程稳态过程动态过程（或过渡过程、瞬态过程、暂态过程）：系统在输入信号作用下，输出量从初始状态到另一个平衡状态的响应过程，可提供系统稳定性、响应速度、阻尼等信息，反映动态性能。CH3系统分析什么是时域分析法？CH3系统分析根据系统的根据系统的微分方程微分方程，求出当，求出当输入为某种输入为某种时间函数时时间函数时，微分方程式的解，即，微分方程式的解，即调节系统的调节系统的时间响应时间响应，从而进一步分析，从而进一步分析系统的稳定性系统的稳定性及其及其快速性和准确性快速性和准确性。。系统的稳定性系统的稳定性11）衰减率）衰减率AC系统偏离稳定态值的第一,第三个波峰幅值（被调量波动幅度）减少的百分数CH3系统分析CCA-系统的稳定性系统的稳定性22）超调量）超调量stpt0tc(t))(c)(ptc)(02.0c)(05.0c或AB%100BAMp%100)()()(cctcMpp暂态过程中输出响应暂态过程中输出响应的最大值超过稳态值的最大值超过稳态值的百分数。的百分数。CH3系统分析系统的快速性系统的快速性CH3系统分析(1)峰值时间tp：响应超过终值到达第一个峰值所需时间(2)上升时间tr：响应从零第一次上升到终值所需时间st)(%)()(cctcΔ%的稳态值响应稳态值(3)调节时间ts：响应到达并保持在允许误差带Δ（如±2％或±5％）内所需的最短时间系统的快速性系统的快速性CH3系统分析系统的准确性CH3系统分析若时间趋于无穷时，系统的输出量不等于输入量或输入量的确定函数，则系统存在稳态误差。通常在阶跃函数、斜坡函数或加速度函数作用下进行测定或计算。)(limteetss理想的控制系统响应情况：超调量小或无超调、上升时间快、调节时间短及稳态误差小或为零。timey期望值控制系统设计的综合指标考虑：CH3系统分析什么是时域分析法？CH3系统分析根据系统的根据系统的微分方程微分方程，求出当，求出当输入为某种输入为某种时间函数时时间函数时，微分方程式的解，即，微分方程式的解，即调节系统的调节系统的时间响应时间响应，从而进一步分析，从而进一步分析系统的稳定性系统的稳定性及其及其动态和稳态品质动态和稳态品质。。一阶系统的时域分析CH3系统分析时间常数其中无源网络的传递函数————进行拉氏变换得：，假定初始状态为零，,11)()()()()(RCRCssRsCtrtcdttdcRC一阶系统的数学模型10CH3系统分析-一阶系统一阶系统的数学模型CH3系统分析-一阶系统010)()()(asabsRsCsG1)(TsksG0001,abkaaT一阶微分方程的一般形式一阶微分方程的传递函数传递函数的标准形式其中:一阶微分方程的一般形式)()()(001trbtcadttdca一阶微分方程的一般形式T称为时间常数一阶系统的时间响应——单位阶跃响应0t,e1c(t)tTTsksksTsksRsGsCssR111)()()(1)(,1)t(r稳态分量输入模态瞬态分量自由模态CH3系统分析-一阶系统一阶系统的时间响应——单位阶跃响应0t,e1c(t)tTTsksksRsGsC1)()()(稳态分量输入模态瞬态分量自由模态CH3系统分析-一阶系统输入函数相关传递函数相关可据此用实验方法测定T，或测定系统是否属于一阶系统——系统辨识•单调曲线，稳态值为K，稳态误差为0。•可以用时间常数T,来度量系统输出量的数值。•响应曲线的初始斜率等于1/T特点响应曲线的斜率随时间推移而下降一阶系统单位阶跃响应曲线0t,e1c(t)tTCH3系统分析-一阶系统k1/Tk1/Tk1/T可见：响应速度与时间常数T有关。稳态性能指标：ess=098.0)(/)(,495.0)(/)(,3632.0)(/)(,ctcTtctcTtctcTt一阶系统性能指标CH3系统分析-一阶系统k1/T输出响应达到稳定值的63.2%所需的时间±5%误差带±2%误差带k)(cEg：3-1，一阶系统如下图所示：其中KK为开环放大倍数，KH为反馈系统。设KK=100，KH=0.1，试求系统的调节时间ts（按±5%误差带）；如果要求ts=0.1s，求反馈系统。CH3系统分析-一阶系统KK/sxKHeb+-y解：)(1)()()(1)()()()(1211sGsGsGsGsGsXsYsGkCH3系统分析-一阶系统系统的闭环函数为：11.0101.01001100)()()(ssssRsCsT=0.1ts=3T=0.3s若要求ts=0.1s，计算KHCH3系统分析-一阶系统1s01.0/11001100)()()(HHHKKKsssRsCsT=0.01/KHKH=0.3二阶系统的时域分析CH3系统分析二阶系统微分方程的一般形式：)()()()()(0101222trbdttdrbtcadttdcadttcdar(t)为输入函数——系统的输入c(t)为输出函数——系统的输出a2,a1,a0,b1,b2——常系数用二阶微分方程描述的控制系统称为二阶系统。用二阶微分方程描述的控制系统称为二阶系统。它是控制系统常见的组成形式，许多高阶系统在一它是控制系统常见的组成形式，许多高阶系统在一定的条件下常近似地用二阶系统来表征。定的条件下常近似地用二阶系统来表征。CH3系统分析-二阶系统的时域分析传递函数012201)()()(asasabsbsRsCsG先考虑传递函数分子部分等于常数的情况01220)()()(asasabsRsCsG)()()()()(010122sRbssRbsCassCasCsa对两边取拉氏变换，求取传递函数拉氏变换的微分性质(零初始条件下)：)(])([sXsdttxdLnnnCH3系统分析-二阶系统的时域分析)()()()()(0101222trbdttdrbtcadttdcadttcda二阶系统传递函数的通用形式01220)()()(asasabsRsCsGa1,a2符号相同0002120n,2,abKaaaaa二阶系统的无阻尼自然振荡频率二阶系统的阻尼比放大系数2222)(nnnssKsG标准式CH3系统分析-二阶系统的时域分析二阶系统单位阶跃响应二阶系统单位阶跃响应特征方程为：特征方程为：0222nnss122,1nns特征根为：特征根为：aacbbscbsas24022二次三项式求根公式：CH3系统分析-二阶系统的时域分析当不同时，特征根和阶跃响应有不同的当不同时，特征根和阶跃响应有不同的形式。形式。01（-∞，0）；0；（0,1）；1；（1，+∞）CH3系统分析-二阶系统的时域分析无阻尼ζ=00th(t)1js平面nns1s2欠阻尼0<ζ<1h(t)0t1j)(nd21n0βs平面s2s1二阶系统阶跃响应小结临界阻尼ζ=10t1h(t)j0s平面s1s2j0s平面s1,20t1h(t)过阻尼ζ>1第一种情况>00<<1欠阻尼响应振荡收敛=1临界阻尼响应单调收敛>1过阻尼响应较慢地单调收敛第三种情况=0=0无阻尼响应等幅振荡122,1nns第二种情况<0-1<<0响应振荡发散<-1响应单调发散CH3系统分析-二阶系统的时域分析随着的增加，随着的增加，c(t)c(t)将从无衰减的周期运动变为有衰减将从无衰减的周期运动变为有衰减的正弦运动，当时的正弦运动，当时c(t)c(t)呈现单调上升运动呈现单调上升运动((无振荡无振荡))。。102468101200.20.40.60.811.21.41.61.82ntc(t)反映实际系统的阻尼情况，故称为阻尼比。反映实际系统的阻尼情况，故称为阻尼比。工程上通常取ζ=0.4～0.8CH3系统分析-二阶系统的时域分析33）当时，）当时，1022,11nnjs阶跃响应为阶跃响应为衰减振荡过程衰减振荡过程欠阻尼情况欠阻尼情况极点的负实部决定了指数衰减的快慢；极点的负实部决定了指数衰减的快慢；n21nd虚部是振荡频率，称为阻尼振荡频率。虚部是振荡频率，称为阻尼振荡频率。)sin(111)(2tetcdt21ndn阶跃响应呈指数衰减（阻尼正弦）振荡，周期性地趋于稳态输出h()——系统稳定。CH3系统分析-二阶系统的时域分析10)(tct)10(欠阻尼情况欠阻尼情况nnncos称为阻尼角称为阻尼角22,11nnjs到虚轴的距离：到虚轴的距离：n到实轴的距离：到实轴的距离：21nd到原点的距离：到原点的距离：n21nj21njn极点分布图极点分布图j00与负实轴夹角：与负实轴夹角：CH3系统分析-典型二阶系统的性能指标0,)sin(11)(2ttetcdtn当时，当时，rtt1)(rtc21arctan，其中上升时间drtrt⒈⒈上升时间上升时间)10(欠阻尼情况欠阻尼情况增大或减小，均能减小，从而加快系统的初始响应速度。nrtCH3系统分析-典型二阶系统的性能指标0,)sin(11)(2ttetcdtn⒉⒉峰值时间峰值时间pt0)cos(1)sin(1)(22pddtpdtntttetedttdcpnpnp21ndpt由于出现在第一次峰值时间，取由于出现在第一次峰值时间，取n=1n=1，有：，有：ptCH3系统分析-典型二阶系统的性能指标%100%100)()()(21ecctcMpp⒊最大超调量pM221211)sin(11)(eetcp00.10.20.30.40.50.60.70.80.910102030405060708090100pM%10021eMp越大，超调量越小越大，超调量越小CH3系统分析-典型二阶系统的性能指标⒋调节时间st可利用包络线进行近似计算可利用包络线进行近似计算当当tt≥≥ttss时时c(t)-c(∞)≤c(∞)×Δ%c(t)-c(∞)≤c(∞)×Δ%%)sin(12tedtn0,)sin(11)(2ttetcdtn响应曲线总在一对包络线之内。响应曲线总在一对包络线之内。包络线为包络线为nst%)1ln(210)(tctstst211tne包络线为包络线为当较小时，近似取，且当较小时，近似取，且1124912.3)02.0ln(3996.2)05.0ln(nst%)1ln(2时当时当5Δ2Δ,3,4nnst所以所以8.00阻尼比是二阶系统的一个重要参数，用它阻尼比是二阶系统的一个重要参数，用它可以间接地判断一个二阶系统的暂态品质。可以间接地判断一个二阶系统的暂态品质。[[总结总结]]1st在的情况下阶跃响应为单调变化曲线，在的情况下阶跃响应为单调变化曲线，无超调和振荡，但长。无超调和振荡，但长。0当时，输出量作等幅振荡或发散振荡，当时，输出量作等幅振荡或发散振荡，系统不能稳定工作。系统不能稳定工作。10在的情况下阶跃响应为衰减振荡，在的情况下阶跃响应为衰减振荡，暂态性能较好。暂态性能较好。[[总结总结]]在欠阻尼情况下工作时，若过小，则在欠阻尼情况下工作时，若过小，则超调量大，调节时间长，暂态性能差。超调量大，调节时间长，暂态性能差。)10(最大超调量只与有关，所最大超调量只与有关，所以一般根据来选择。以一般根据来选择。%10021eMppM。，一定时，当，snnnstt)3(4或在之间，调节时间和超调量都较小。在之间，调节时间和超调量都较小。工程上常取作为设计依据，称为最佳工程上常取作为设计依据，称为最佳阻尼比。阻尼比。8.0~4.0707.021[[解解]]：：①闭环传递函数为：①闭环传递函数为：)(sR)1(TssK)(sC[[例例]]：如图所示系统，：如图所示系统，试求：①和试求：①和;②;②和和③③若要求，若要求，当当TT不变时不变时KK=?=?sTK25.016，pM%16pMnst2222221)(nnnssTKsTsTKKsTsKsTTKnn12225.025.0162121)/(825.016KTsradTKn③③0.5，解得%,16%10021eMp当当TT不变时，不变时，T=0.25T=0.25，，45.025.0414122TK②②%44%10021eMp)%5(,5.1825.033)%2(,2825.044误差带取误差带取sstnns劳斯稳定判据CH3系统分析一、一、稳定的基本概念稳定的基本概念稳定是控制系统的稳定是控制系统的重要性能重要性能，也是系统，也是系统能够正常运行的能够正常运行的首要条件首要条件。。设系统处于某一平衡状态。在外部干扰作用设系统处于某一平衡状态。在外部干扰作用的影响下，离开了该平衡状态。当的影响下，离开了该平衡状态。当干扰作用消失干扰作用消失后后，如果经过足够长的时间它能，如果经过足够长的时间它能自动回复自动回复到原来到原来的的初始平衡状态初始平衡状态，则称这样的系统为稳定的系统。，则称这样的系统为稳定的系统。否则为不稳定的系统。否则为不稳定的系统。注意：以上定义只适用于线性定常系统。注意：以上定义只适用于线性定常系统。CH3系统分析-劳斯稳定判据注意：注意：稳定性是控制系统自身的固有特性，取决于系统本稳定性是控制系统自身的固有特性，取决于系统本身的结构和参数，与输入无关。身的结构和参数，与输入无关。二、线性定常系统稳定的必要而不充分条件二、线性定常系统稳定的必要而不充分条件系统的特征方程的全部系统同号（但不为系统的特征方程的全部系统同号（但不为00）。）。CH3系统分析-劳斯稳定判据01110nnnnasasasa在利用劳斯判据对系统的稳定性判断前，先做该判断线性定常系统稳定的充要条件线性定常系统稳定的充要条件系统特征方程的根（即闭环极系统特征方程的根（即闭环极点）全部具有负实部。点）全部具有负实部。或者说，或者说，特征方程的根应全部位于特征方程的根应全部位于ss平平面的左半平面。面的左半平面。稳稳定定区区不不稳稳定定区区临临界界稳稳定定ss平面平面j0注意：注意：稳定性稳定性是线性定常系统的一个是线性定常系统的一个属性，属性，只与系统本身的结构参数有关只与系统本身的结构参数有关，与，与输入输输入输出信号无关出信号无关，与，与初始条件无关初始条件无关；；只与极点有关只与极点有关，，与零点无关。与零点无关。CH3系统分析-劳斯稳定判据,,00110aasasa对于对于一阶系统一阶系统，只要，只要都大于零，系统是稳定的。都大于零，系统是稳定的。10,aa对于对于二阶系统二阶系统，，0202112,1212024,0aaaaasasasa只要都大于零，系统稳定。（负只要都大于零，系统稳定。（负实根或实部为负）实根或实部为负）210,,aaa因此，可以根据求解特征方程式的根来因此，可以根据求解特征方程式的根来判断系统稳定与否。判断系统稳定与否。可见，可见，对于一阶和二阶线性定常系统，系统稳对于一阶和二阶线性定常系统，系统稳定的充要条件是其特征方程式的各项系数均为正值。定的充要条件是其特征方程式的各项系数均为正值。CH3系统分析-劳斯稳定判据对于三阶或以上系统，特征方程式的各项对于三阶或以上系统，特征方程式的各项系数均为正值只是系统稳定的必要条件而非充系数均为正值只是系统稳定的必要条件而非充分条件。分条件。高阶系统特征方程式的求解很麻烦，高阶系统特征方程式的求解很麻烦，用代用代数稳定判据就可以不必求解出特征根而判断出数稳定判据就可以不必求解出特征根而判断出系统特征根实部的正负，从而判断系统是否稳系统特征根实部的正负，从而判断系统是否稳定。定。CH3系统分析-劳斯稳定判据使用劳斯判据判断系统稳定性的步骤如下：使用劳斯判据判断系统稳定性的步骤如下：1.1.列出系统特征方程式列出系统特征方程式01110nnnnasasasa式中各项系数均为实数，且使式中各项系数均为实数，且使aa00>0>0。。2.2.判断各项系数是否都为正值判断各项系数是否都为正值特征方程式各项系数均为正值是系统特征方程式各项系数均为正值是系统稳定的必要条件。稳定的必要条件。一、劳斯判据一、劳斯判据CH3系统分析-劳斯稳定判据3.3.如果所有系数都是正的，则可以将多项式系数如果所有系数都是正的，则可以将多项式系数按下列格式列出劳斯阵列表（劳斯表）按下列格式列出劳斯阵列表（劳斯表）01110nnnnasasasa劳斯表的前两行由特征方劳斯表的前两行由特征方程的系数组成。程的系数组成。第一行为第一行为11，，33，，55，，……项系数组成，项系数组成，第二行为第二行为22，，44，，66，，……项系数组成。项系数组成。1321321321531420gdddcccbbbaaaaaa04321ssssssnnnnnCH3系统分析-劳斯稳定判据13021131201aaaaaaaaaab15041151402aaaaaaaaaab17061171603aaaaaaaaaab1321321321531420gdddcccbbbaaaaaa04321ssssssnnnnnCH3系统分析-劳斯稳定判据11231121311bababbbbaac11351131512bababbbbaac11471141713bababbbbaac用同样的方法，求取表中其它行的系数，用同样的方法，求取表中其它行的系数，一直进行到第一直进行到第n+1n+1行（行（ss00行）为止。行）为止。为了简化数值计算，可以用一个正数去除或乘某一行为了简化数值计算，可以用一个正数去除或乘某一行的各项，并不改变稳定性的结论。的各项，并不改变稳定性的结论。1321321321531420gdddcccbbbaaaaaa04321ssssssnnnnnCH3系统分析-劳斯稳定判据4.4.根据劳斯表中第一列各元素的符号，用劳斯判根据劳斯表中第一列各元素的符号，用劳斯判据来判断系统的稳定性据来判断系统的稳定性劳斯判据的内容如下：劳斯判据的内容如下：系统稳定的充要条件是劳斯表第一列各元系统稳定的充要条件是劳斯表第一列各元素均为正数。素均为正数。如果第一列系数中有负数，则系如果第一列系数中有负数，则系统不稳定，统不稳定，且第一列系数符号的改变次数等于且第一列系数符号的改变次数等于特征方程式的根在特征方程式的根在ss平面右半部分的个数。平面右半部分的个数。CH3系统分析-劳斯稳定判据5.5.两种特殊情况两种特殊情况11）劳斯表某一行中的第一个系数为零，或某）劳斯表某一行中的第一个系数为零，或某一行系数全部为零。一行系数全部为零。但其余各项不全为零或者但其余各项不全为零或者没有其余项。这时系统处于没有其余项。这时系统处于不稳定或临界稳定不稳定或临界稳定状态状态。。[[处理方法处理方法]]用一个很小的正数用一个很小的正数εε来代替这来代替这个零，并据此计算出阵列中的其余各项。个零，并据此计算出阵列中的其余各项。如果上下两项的符号相同，则说明系统存在一如果上下两项的符号相同，则说明系统存在一对虚根，系统处于临界稳定状态；对虚根，系统处于临界稳定状态；如果不同，表明有一次符号变化，系统不稳定。如果不同，表明有一次符号变化，系统不稳定。CH3系统分析-劳斯稳定判据0122234ssss若则若则220例：特征方程式为：，试判例：特征方程式为：，试判断稳定性。断稳定性。[[解解]]：劳斯表为：：劳斯表为：故第一列有两次符号变化，故第一列有两次符号变化，ss右半平面有两个极点，右半平面有两个极点，系统不稳定。系统不稳定。001002202)(002211101234sssssCH3系统分析-劳斯稳定判据22）劳斯表某一行中所有的系数都为零，）劳斯表某一行中所有的系数都为零，表明在表明在ss平面平面内存在大小相等但位置径向相反的根，内存在大小相等但位置径向相反的根，至少要下述几种至少要下述几种情况之一出现，情况之一出现，如：大小相等，符号相反的一对实根；如：大小相等，符号相反的一对实根；或一对共轭虚根；或对称于实轴的两对共轭复根。或一对共轭虚根；或对称于实轴的两对共轭复根。大小相等符号大小相等符号相反的实根相反的实根共轭虚根共轭虚根对称于实轴的对称于实轴的两对共轭复根两对共轭复根CH3系统分析-劳斯稳定判据22）劳斯表某一行中所有的系数都为零）劳斯表某一行中所有的系数都为零[[处理方法处理方法]]可将不为零的最后一行的系数组可将不为零的最后一行的系数组成辅助方程，并以此辅助方程式对成辅助方程，并以此辅助方程式对ss求导所得求导所得方程的系数代替全零的行。方程的系数代替全零的行。大小相等，位置径向相反的根可以通过求大小相等，位置径向相反的根可以通过求解辅助方程得到，而且根的数目总是偶数（辅解辅助方程得到，而且根的数目总是偶数（辅助方程应为偶次数的）。助方程应为偶次数的）。CH3系统分析-劳斯稳定判据[[例例]]：：0161620128223456ssssss3456ssss0000016122016122162081168168168168辅助方程为：辅助方程为：08624ss01243ss求导得：求导得：用用11，，33，，00代替全零行即可。代替全零行即可。033ss或或0123ssss83183031第一列元素都大于零，说明第一列元素都大于零，说明ss右半平面没有闭环极点。右半平面没有闭环极点。但出现了全零行，表明系统有共轭虚数极点。但出现了全零行，表明系统有共轭虚数极点。CH3系统分析-劳斯稳定判据[[例例]]：：0161620128223456ssssss0)4)(2(22ss辅助方程为：辅助方程为：08624ss此时系统是临界稳定的。此时系统是临界稳定的。控制工程上认为是不稳定的。控制工程上认为是不稳定的。系统的共轭虚数极点可由辅助方程求出。系统的共轭虚数极点可由辅助方程求出。2,24,32,1jsjs解得：解得：CH3系统分析-劳斯稳定判据应用一：应用一：判定控制系统的稳定性判定控制系统的稳定性例：系统的特征方程为：，例：系统的特征方程为：，判断系统的稳定性。判断系统的稳定性。05432234ssss[[解解]]：劳斯表如下：：劳斯表如下：56514253101234sssss因为，但劳斯因为，但劳斯表第一列不全为正，所以，系统表第一列不全为正，所以，系统不稳定。不稳定。由于劳斯阵第一列有两次符号变由于劳斯阵第一列有两次符号变化，所以系统在化，所以系统在ss右半平面有两右半平面有两个极点。个极点。)4~0(,0iaiCH3系统分析-劳斯稳定判据应用二：应用二：分析系统参数变化对稳定性的影响分析系统参数变化对稳定性的影响利用代数稳定性判据还可以讨论个别参数对利用代数稳定性判据还可以讨论个别参数对稳定性的影响，从而求得这些参数的取值范围。稳定性的影响，从而求得这些参数的取值范围。若讨论的参数为开环放大系数若讨论的参数为开环放大系数KK，则使系统稳，则使系统稳定的最大定的最大KK称为临界放大系数称为临界放大系数KKLL。。例：已知系统的结构图，试确定系统的临界放大系数。例：已知系统的结构图，试确定系统的临界放大系数。解：闭环传递函数为：解：闭环传递函数为：KsssKsssKsssKs158)5)(3(1)5)(3()(23特征方程为：特征方程为：015823Ksss)5)(3(sssK)(sR)(sC劳斯表：劳斯表：KKKssss812081510123要使系统稳定，必须要使系统稳定，必须①①系数皆大于系数皆大于00，，0K②②劳斯阵第一列皆大于劳斯阵第一列皆大于001200012008120KKKK有120LK所以，临界放大系数所以，临界放大系数特征方程为：特征方程为：015823Ksss应用三：确定系统的相对稳定性（稳定裕应用三：确定系统的相对稳定性（稳定裕量）量）利用劳斯稳定性判据确定的是系统稳定或不稳利用劳斯稳定性判据确定的是系统稳定或不稳定，即定，即绝对稳定性绝对稳定性。在实际系统中，往往需要知道。在实际系统中，往往需要知道系统离临界稳定有多少裕量，这就是系统离临界稳定有多少裕量，这就是相对稳定性或相对稳定性或稳定裕量问题稳定裕量问题。。jaa:给定稳定度应用三：确定系统的相对稳定性（稳定裕应用三：确定系统的相对稳定性（稳定裕量）量）作的垂线，若系统的极点都在该线作的垂线，若系统的极点都在该线的左边，则称该系统具有的稳定裕度。的左边，则称该系统具有的稳定裕度。一般一般说，越大，稳定程度越高。可用代说，越大，稳定程度越高。可用代入特征方程，得以入特征方程，得以zz为变量的新的特征方程，为变量的新的特征方程，用劳斯判据进行判稳。若稳定，则称系统具有用劳斯判据进行判稳。若稳定，则称系统具有的稳定裕度。的稳定裕度。asaazsaaja例：系统特征方程为：。例：系统特征方程为：。068523sss022,06)1(8)1(5)1(2323zzzzzz即022110123zzzz1z行全为零，以它上面的行组行全为零，以它上面的行组成辅助方程。对辅助成辅助方程。对辅助方程求导，用其系数代替行，方程求导，用其系数代替行，其系数为其系数为11。。1z0222z12,1jz辅助方程的解为有一对共轭虚根，所以系统的稳定裕量恰为有一对共轭虚根，所以系统的稳定裕量恰为11。。用劳斯判据可知它是稳定的。判断它是否具有稳用劳斯判据可知它是稳定的。判断它是否具有稳定裕量定裕量aa=1=1。。1zs令则：令则：1122调节系统如下图所示：若要求闭环特征方程的实部小于-1，问K值应取什么范围？如果要求实部均小于-2，情况又如何？1/s(s+3)(s+6)R(s)eb+-C(s)KCH3系统分析-劳斯稳定判据解：该系统的闭环传递函数为：0)10(36,10189189)()()(1213112323KsssssKsssKsssKsRsCsG代入上式，得：令闭环特征方程为：CH3系统分析-劳斯稳定判据10-62810-63101112131KKKssss00628010-KKK1028KCH3系统分析-劳斯稳定判据若要求系统特征根的实部均小于-2，令s=s1-2,得如下新的特征方程：CH3系统分析0)8(6312131KsssS1前系数为负，无论K取多少，系统特征根的实部不可能小于-2CH3系统分析-劳斯稳定判据作业：调节系统如下图所示：(1)确定系统稳定时，K值的范围；（2）如果要求闭环系统的根全部位于s=-1垂线之左，K值范围应取多大？1/s(0.1s+1)(0.2s+1）R(s)eb+-C(s)KCH3系统分析-劳斯稳定判据北京理工大学珠海学院热工过程自动调节系统的分析和整定4热工过程自动调节系统的分析和整定热工对象的动态特性三种基本调节规律PID调节器单回路调节系统和串级调节的整定方法热工对象的动态特性控制系统设计任务：根据被控对象的动态特性，选择和设计控制器使系统满足规定的性能指标。被控对象的动态特性：1）不振荡环节2）有无自平衡能力3）被调量与调节对象的关系选择控制：1）PID控制器2）P、PI、PD控制器设计控制器：调节比例带、积分时间、微分时间三个参数，使系统性能最优热工对象的动态特性热工对象的共同特点：1）不振荡环节（安全运行的要求）；2）热工对象内部过程的物理性能比较复杂通过实验来获得对象的动态特性tthBAt0t0t0hh有自平衡能力无自平衡能力阶跃响应（1）、具有一个被调量的对象µ1C1λ1λ2通道：对象的输入量至输出量的信号联系；控制通道：控制作用到输出量(被调量)的信号联系；干扰通道：干扰作用至输出量的信号联系；热工对象的动态特性3）被调量与调节对象的关系热工对象的动态特性内扰:经过调节通道作用到对象上的扰动称为“内部扰动”或“基本扰动”；外扰:经过干扰通道作用到对象上的扰动称为“外部扰动”;不同信号通道的传递函数(或微分方程)不同调节通道干扰通道干扰通道外扰λ2外扰λ3内扰λ1被调量C调节对象热工对象的动态特性调节通道干扰通道干扰通道调节作用µ外扰λ2外扰λ3内扰λ1被调量C调节对象扰动是随机的、短暂的、一次发生的，它的动态特性只影响被调量的幅值调节通道的动态特性是整定调节系统的依据认为无自平衡能力对象的自平衡率为ρ=0，那么所有的热工对象都可以用以下三个特征参数来描述1）飞升速度ε：在单位阶跃扰动下，输出y(t)的最大变化速度。2）自平衡率ρ：表征对象的自平衡能力3）延迟时间τ：y(t)的渐近线在时间轴上所截取的长度。用特征参数近似表示对象的动态特性ty(t)ty(∞)x0τTcy(t)tτTax0三种基本调节作用分析4.2调节规律和调节器1）比例（P）调节规律)(1)()(teteKtmp1)(pKsG微分方程传递函数特点2：m(t)和e(t)有一一对应的关系，调节的结果是被调量存在着静态偏差。特点1：无惯性、无延迟、动作快，对干扰能及时并有很强的抑制作用。动作规律：m(t)和e(t)的大小成比例，偏差e(t)的变化速度越大，m(t)的变化速度越大三种基本调节作用分析2）积分（I）调节规律tItIdtteTdtteKtm00)(1)()(4.2调节规律和调节器微分方程传递函数s1s)s(IITKG特点2：调节作用随着时间逐渐增强，相对迟缓，恶化了动态品质，使过渡过程振荡加剧，不稳定。特点1：可以消除静态偏差动作规律：只要e(t)存在，dm(t)/dt不为零，执行机构会不停的动作，且e(t)越大，dm(t)/dt越大，只有当e(t)为零时，dm(t)/dt为零，调节过程才结束，系统才平衡很少单独使用三种基本调节作用分析3）微分（D）调节规律dttdeTdttdeKtmDD)()()(4.2调节规律和调节器微分方程传递函数sTsGD)(特点2：对恒定不变的偏差没有克服能力，不能满足调节的要求。特点1：具有超前的调节作用，有利于克服动态偏差动作规律：调节开始时，e(t)小，但变化速度快，可使调节机构产生较大的位移，调节结束时，de(t)/dt为零时，m(t)为零，执行机构会停止动作。不能够单独使用不能够单独使用P调节器:只有比例调节的作用)(1)()(teteKtP1)()()(PKsEssG4.2调节规律和调节器特点：调节速度快，但是有静态偏差如果要克服系统的静态偏差可增加积分调节比例调节器的阶跃响应曲线t00e00e01emmPI调节器：具有比例和积分调节的作用])(1)([])()([)(00tIPtPIPdtteTteKdtteKKteKt)11(1)11()()()(sTsTKsEssGIIP4.2调节规律和调节器])(1)([1)(0tIdtteTtet有两个调节参数，KP和KI或δ和TI,当TI趋近于∞时，就变成比例调节器，当TI趋近于0时，就变成积分调节器积分时间TI越小，积分作用越强，比例带δ会影响比例作用和积分作用的强弱。])(1)([1)(0tIdtteTtett11)(00eTetI4.2调节规律和调节器特点：调节速度快，无静态偏差，有动态偏差如果要克服系统的动态偏差可增加微分调节0ett0me0PI调节器的阶跃响应曲线0eiT0e00012T11)(eeTetIIt=TIPD调节器：具有比例和微分调节的作用])()([1])()([)(dttdeTtedttdeTteKtDDP)1(1)1()()()(sTsTKsEssGDDP4.2调节规律和调节器有两个调节参数，KP和KD或δ和TD,当TD趋近于0时，就变成比例调节器，当TD趋近于∞时，就变成微分调节器积分时间TD越大，微分作用越强，比例带δ会影响比例作用和微分作用的强弱。特点：调节速度快，动态偏差小，有静态偏差如果要克服系统的静态偏差可增加积分调节比例微分作用调节器的响应曲线0e0ett0e0adtdedTatt0e0dT21dT(a)(b)4.2调节规律和调节器比例微分作用调节器的响应曲线0e0ett0e001eKDdT)1(632.0PK(c)4.2调节规律和调节器实际微分环节])1(1[1)(0DTtDeKetmPID调节器4.2调节规律和调节器控制器调节对象E(s)µ(s)C(s)R(s)λ单回路调节系统的组成框图PID调节器的组成框图P、I、D并联KpKI/sKDsE(s)µ(s)调节器+++)()()()(321sGsGsGsGKpKI/sKDsE(s)µ(s)调节器+++pKsG)(sKGI/)s(4.2调节规律和调节器sKsGD)()11(111)(sTsTsKKsKKKsKsKKsGDIPDPIPDIpPID）（微分时间积分时间：比例带::DITT比例调节积分调节微分调节PID调节器4.2调节规律和调节器0e0ett0e001eKDPIDDPI实际PID调节器的阶跃响应曲线4.3系统的整定分析控制器调节对象E(s)µ(s)C(s)R(s)λ调节系统的性能取决与比例带、积分时间、微分时间可用理论计算和实验两种方法得到最优参数简单系统简单系统复杂系统工程整定法4.3比例带、积分时间、微分时间对系统调节品质的影响一、比例带对系统调节品质的影响1)()()(PKsEssG综上所述，采用比例调节器的单回路反馈控制系统随着比例系数KP的增加（或比例带δ的减小）,控制系统的稳定性下降,控制过程时间增长，被调量的动态偏差和静态偏差减小。衰减率（0.75~0.9）选择较小的静态偏差和动态偏差4.3系统的整定分析4.3比例带、积分时间、微分时间对系统调节品质的影响)11(1)(sTsGIR二、积分时间对系统调节品质的影响由于积分作用的存在，被调量的静态偏差为00])()11(1)([lim)]()([lim0000sGsTsGsGssReIss积分作用加入后会使衰减率减小，为了保持原来的衰减率，必须将比例带的数值适当提高。引入积分时间会恶化动态品质4.3系统的整定分析4.3比例带、积分时间、微分时间对系统调节品质的影响三、微分时间对系统调节品质的影响)11(1)(sTsTsGDIR积分作用与微分作用配合适当可保证系统稳定，积分时间一般取微分时间的4倍微分作用可以有效改善系统的动态品质4.3系统的整定分析4.4单回路调节系统的整定一、临界比例带法在纯比例作用下，将系统投入闭环运行，不断改变比例带δ的数值使调节系统产生等幅振荡，并记录对应的比例带和振荡周期，称为临界比例带δc和临界振荡周期Tc，然后根据这两个参数得到系统所希望的衰减率时的其他整定参数。0,DITT将比例带δ置于较大的数值查表得到适用于可能出现等幅振荡、等幅振荡幅度不大和振荡周期较长的调节系统。4.3系统的整定分析4.4单回路调节系统的整定二、衰减曲线法在纯比例作用下将系统投入闭环运行，不断改变比例带δ的数值使调节系统达到所要求的衰减率φ(φ=0.75),并记录对应比例带δs，Ts来整定调节器的其他参数。0,DITT将比例带δ置于较大的数值查表得到4.3系统的整定分析4.4单回路调节系统的整定三、图表整定法采用图表整定法首先对被调对象作阶跃扰动试验，记录阶跃响应曲线，求取阶跃响应曲线上的特征参数：自平衡率ρ、飞升速度ε、迟延时间τ和时间常数Tc,然后通过整定参数表4-8的计算公式计算调节器的各整定参数。4.3系统的整定分析4-5串级系统的整定电厂锅炉过热汽温控制4-5串级系统的整定1.什么是串级系统？采用不止一个控制器，而且控制器间相串联，一个控制器的输出作为另一个控制器的设定值的系统。主控制器副控制器调节阀副参数测量变送副对象主对象一次扰动二次扰动主被控参数副被控参数＋－＋－主参数测量变送y1,spy2,spy2ym2y1ym1导前区惰性区主参数（主变量）：对象的主控参数副参数（副变量）：为了稳定主参数而引入的辅助参数主对象：由主参数表征其特性的生产过程副对象：由副参数为输出的生产过程，副回路所包含的对象。4-5串级系统的整定主调节器（主控制器）：按主参数的测量值与给定值的偏差进行工作的调节器。副调节器（副控制器）：按副参数的测量值与主调节器输出的偏差进行工作的调节器。主回路与副回路串级控制系统的基本术语一次扰动：不包括在副回路内的扰动。二次扰动：包括在副回路内的扰动。4-5串级系统的整定串级控制系统的基本术语3.串级调节系统的分析1）能有效的减小在二次扰动下的动态偏差副回路具有快速作用2）对一次扰动的偏差也有一定的改善作用3）串级系统具有一定的适应能力4-5串级系统的整定4.串级系统的设计原则串级系统要实现的调节功能：当发生二次扰动时，内回路应迅速地消除扰动作用。当发生一次扰动时，内回路应作为外回路的随动系统，迅速的配合主调节器，主调节器应能实现无偏差调节。原则：1）副参数的选择应使副回路的时间常数小，反应灵敏。2）副回路应包含被控制对象所受到的主要干扰。3）主副回路工作频率应适当匹配，4-5串级系统的整定为副回路的振荡周期为主回路的振荡周期，1212)10~3(ddddTTTT5.串级系统的调节器的选则4-5串级系统的整定主控制器副控制器调节阀副参数测量变送副对象主对象一次扰动二次扰动主被控参数副被控参数＋－＋－主参数测量变送y1,spy2,spy2ym2y1ym1积分作用PI,PID比例作用，微分作用P,PD主控制器：工艺上对主变量要求比较严格,不允许有余差.主回路是定值系统,为了主变量的稳定,主控制器一般选用PI控制.但当对象控制通道容量滞后较大时,为克服容量滞后则可采用PID控制.4-5串级系统的整定副控制器：副控制器一般采用P控制器，因当控制器有微分作用时,一旦主控制器的输出稍有变化,控制阀就将大幅度的变化,对控制不利.只有当副对象容量滞后较大时,才增加微分(D)作用5.串级系统的调节器的选则6.串级系统的整定对串级系统“先内后外”整定法，对主、副回路可采用“临界比例带法”；“衰减曲线法”；“图表整定法”。Eg：以衰减曲线法整定串级系统1）先整定内回路4-5串级系统的整定0,DITT设置副回路参数δ1置于较大的数值（纯比例作用），将系统投入闭环运行，并施加阶跃扰动，当系统达到所要求的衰减率(φ=0.75)时，记录比例带δs1和衰减振荡周期Ts1设置主调节器δ2=100%TD1=02）整定外回路4-5串级系统的整定0,11DITT设置主回路参数δ2置于较大的数值（纯比例作用），将系统投入闭环运行，并施加阶跃扰动，当系统达到所要求的衰减率(φ=0.75)时，记录比例带δs2和衰减振荡周期Ts2。设置副调节器参数δ1=δs1（纯比例作用）TD1=03）选取主、副调节器的各整定参数依据主调节器的比例带δs2和衰减振荡周期Ts2和副调节器的比例带δs1和衰减振荡周期Ts1，查表查表4-9（p151）,计算φ=0.75时的调节器参数值。