《三角函数章末整体提升》高一年级下册PPT课件.pptx

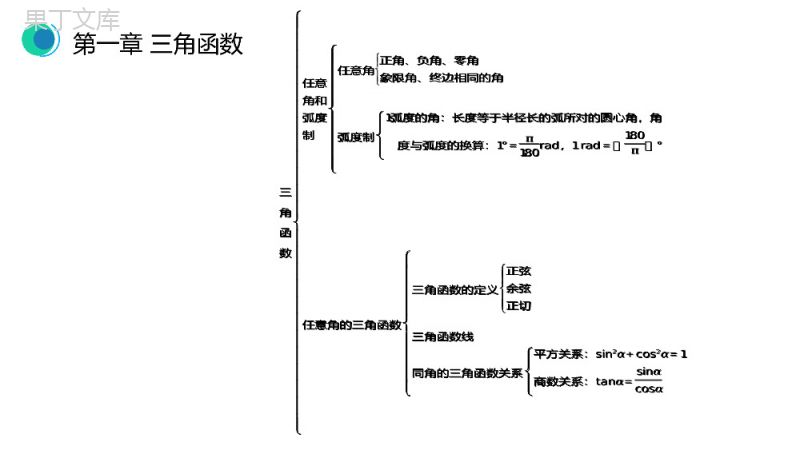
章末整体提升第一章三角函数目录CONTENT01知识结构02专题探究知识结构第一章三角函数01PARTONE第一章三角函数三角函数任意角和弧度制任意角正角、负角、零角象限角、终边相同的角弧度制1弧度的角：长度等于半径长的弧所对的圆心角，角度与弧度的换算：1°＝π180rad，1rad＝180π°任意角的三角函数三角函数的定义正弦余弦正切三角函数线同角的三角函数关系平方关系：sin2α＋cos2α＝1商数关系：tanα＝sinαcosα三角函数任意角和弧度制任意角正角、负角、零角象限角、终边相同的角弧度制1弧度的角：长度等于半径长的弧所对的圆心角，角度与弧度的换算：1°＝π180rad，1rad＝180π°任意角的三角函数三角函数的定义正弦余弦正切三角函数线同角的三角函数关系平方关系：sin2α＋cos2α＝1商数关系：tanα＝sinαcosα第一章三角函数三角函数三角函数的诱导公式公式一～四：α＋2kπk∈Z，－α，π±α的三角函数值等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号公式五、六：π2±α的正余弦函数值，分别等于α的余弦正弦函数值，前面加上一个把α看成锐角时原函数值的符号三角函数的图象与性质图象正弦曲线、余弦曲线、正切曲线图象特征性质周期性奇偶性单调性最大、最小值三角函数三角函数的诱导公式公式一～四：α＋2kπk∈Z，－α，π±α的三角函数值等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号公式五、六：π2±α的正余弦函数值，分别等于α的余弦正弦函数值，前面加上一个把α看成锐角时原函数值的符号三角函数的图象与性质图象正弦曲线、余弦曲线、正切曲线图象特征性质周期性奇偶性单调性最大、最小值第一章三角函数三角函数函数y＝Asinωx＋φ的图象A、ω、φ对函数图象的影响图象画法五点法变换法三角函数模型的简单应用三角函数函数y＝Asinωx＋φ的图象A、ω、φ对函数图象的影响图象画法五点法变换法三角函数模型的简单应用专题探究第一章三角函数02PARTTWO第一章三角函数三角函数的定义及诱导公式在中学数学的学习中主要有两方面的作用：一是以集合的交、并、补运算为载体，考查三角函数值在各象限内的符号、终边相同的角及象限角等基础知识．二是考查诱导公式在三角函数求值、化简、证明和三角恒等变换中的应用．专题一三角函数的概念和诱导公式⇨第一章三角函数典例1已知角α终边上一点P的坐标为(sin5π6，cos5π6)，则角α的最小正值是()A．5π6B．2π3C．5π3D．11π6C[思路分析]利用特殊角的三角函数值判断点P所在的象限，再利用特殊角的三角函数值求解，也可以利用三角函数定义和诱导公式求解．已知角α终边上一点P的坐标为(sin5π6，cos5π6)，则角α的最小正值是()A．5π6B．2π3C．5π3D．11π6[思路分析]利用特殊角的三角函数值判断点P所在的象限，再利用特殊角的三角函数值求解，也可以利用三角函数定义和诱导公式求解．第一章三角函数[解析]方法一：由sin5π6＝12，cos5π6＝－32可知点P的坐标为(12，－32)，故第四象限角，且tanα＝－3，所以α＝5π3.方法二：由三角函数定义知，sinα＝cos5π6＝cos(π2＋π3)＝－sinπ3＝sin(－π3)，与－π3有相同正弦值的第四象限的最小正角是5π3.[解析]方法一：由sin5π6＝12，cos5π6＝－32可知点P的坐标为(12，－32)，故第四象限角，且tanα＝－3，所以α＝5π3.方法二：由三角函数定义知，sinα＝cos5π6＝cos(π2＋π3)＝－sinπ3＝sin(－π3)，与－π3有相同正弦值的第四象限的最小正角是5π3.第一章三角函数『规律总结』由三角函数的定义可知，单位圆上任意一点的坐标为(cosθ，sinθ)即x＝cosθy＝sinθ，θ∈[0,2π]．『规律总结』由三角函数的定义可知，单位圆上任意一点的坐标为(cosθ，sinθ)即x＝cosθy＝sinθ，θ∈[0,2π]．第一章三角函数专题二利用三角函数及关系化简、证明、计算⇨三角函数的定义及同角三角函数的基本关系在高考中应用比较多，结合化简、求值、证明进行考查，注意公式sin2α＋cos2α＝1和tanα＝sinαcosα及变形公式的灵活运用．三角函数的定义及同角三角函数的基本关系在高考中应用比较多，结合化简、求值、证明进行考查，注意公式sin2α＋cos2α＝1和tanα＝sinαcosα及变形公式的灵活运用．第一章三角函数已知－π20，∴sinx－cosx<0.故sinx－cosx＝－75.[解析](1)将sinx＋cosx＝15两边平方得2sinxcosx＝－2425，∴(sinx－cosx)2＝1－2sinxcosx＝4925.∵－π20，∴sinx－cosx<0.故sinx－cosx＝－75.第一章三角函数(2)sinxcosx＋sin2x1－tanx＝sinxsinx＋cosx1－sinxcosx＝cosxsinxsinx＋cosxcosx－sinx＝－1225×1575＝－12175.(2)sinxcosx＋sin2x1－tanx＝sinxsinx＋cosx1－sinxcosx＝cosxsinxsinx＋cosxcosx－sinx＝－1225×1575＝－12175.第一章三角函数『规律总结』(1)sinα±cosα，sinαcosα之间可通过(sinα±cosα)2＝1±2sinαcosα知一求二，有关sin3α±cos3α，sin4α±cos4α，sin6α±cos6α，tanα＋1tanα等化简都与此基本变形有关．(2)统一函数名称，统一角，统一运算结构是三角函数、求值、变形的常用方法．『规律总结』(1)sinα±cosα，sinαcosα之间可通过(sinα±cosα)2＝1±2sinαcosα知一求二，有关sin3α±cos3α，sin4α±cos4α，sin6α±cos6α，tanα＋1tanα等化简都与此基本变形有关．(2)统一函数名称，统一角，统一运算结构是三角函数、求值、变形的常用方法．第一章三角函数求三角函数的值域(最值)可分为几类：(1)是y＝Asin(ωx＋φ)＋k类型的，应利用其图象与性质、数形结合求解．(2)是可化为以三角函数为元的二次函数类型，应确定三角函数的范围，再用二次函数求解．(3)利用几何意义求解等．专题三三角函数的值域与最值问题⇨第一章三角函数典例3已知函数y＝asin(2x＋π6)＋b在x∈[0，π2]上的值域为[－5,1]，求a、b的值．[思路分析]先由x的范围确定sin(2x＋π6)的范围，再根据a的符号，讨论a、b的值．已知函数y＝asin(2x＋π6)＋b在x∈[0，π2]上的值域为[－5,1]，求a、b的值．[思路分析]先由x的范围确定sin(2x＋π6)的范围，再根据a的符号，讨论a、b的值．第一章三角函数[解析]∵x∈[0，π2]，∴2x＋π6∈[π6，76π]，sin(2x＋π6)∈[－12，1]．∴当a>0时，a＋b＝1，－a2＋b＝－5，解得a＝4，b＝－3；当a<0时，－12a＋b＝1，a＋b＝－5，解得a＝－4，b＝－1.∴a、b的取值分别是4、－3或－4、－1.[解析]∵x∈[0，π2]，∴2x＋π6∈[π6，76π]，sin(2x＋π6)∈[－12，1]．∴当a>0时，a＋b＝1，－a2＋b＝－5，解得a＝4，b＝－3；当a<0时，－12a＋b＝1，a＋b＝－5，解得a＝－4，b＝－1.∴a、b的取值分别是4、－3或－4、－1.第一章三角函数『规律总结』本题是先由定义域确定正弦函数y＝sin(2x＋π6)的值域，但对整个函数的最值的取得与a有关系，故对a进行分类讨论．『规律总结』本题是先由定义域确定正弦函数y＝sin(2x＋π6)的值域，但对整个函数的最值的取得与a有关系，故对a进行分类讨论．第一章三角函数设a≥0，若y＝cos2x－asinx＋b的最大值为0，最小值为－4，试求a、b的值．[思路分析]通过换元化为一元二次函数最值问题求解．典例4[解析]原函数变形为y＝－(sinx＋a2)2＋1＋b＋a24.当0≤a≤2时，－a2∈[－1,0]，∴ymax＝1＋b＋a24＝0.①ymin＝－(1＋a2)2＋1＋b＋a24＝－4②[解析]原函数变形为y＝－(sinx＋a2)2＋1＋b＋a24.当0≤a≤2时，－a2∈[－1,0]，∴ymax＝1＋b＋a24＝0.①ymin＝－(1＋a2)2＋1＋b＋a24＝－4②第一章三角函数由以上两式①②，得a＝2，b＝－2，舍a＝－6(与0≤a≤2矛盾)．当a>2时，－a2∈(－∞，－1)，∴ymax＝－(－1＋a2)2＋1＋b＋a24＝0.③ymin＝－(1＋a2)2＋1＋b＋a24＝－4.④由以上两式③④，得a＝2，不适合a>2，∴应舍去．综上知，只有一组解a＝2，b＝－2.由以上两式①②，得a＝2，b＝－2，舍a＝－6(与0≤a≤2矛盾)．当a>2时，－a2∈(－∞，－1)，∴ymax＝－(－1＋a2)2＋1＋b＋a24＝0.③ymin＝－(1＋a2)2＋1＋b＋a24＝－4.④由以上两式③④，得a＝2，不适合a>2，∴应舍去．综上知，只有一组解a＝2，b＝－2.第一章三角函数『规律总结』一元二次函数区间最值问题含有参数时，应按照对称轴与区间的相对位置去讨论．第一章三角函数专题四正弦函数与余弦函数的对称性问题⇨正弦函数y＝sinx，余弦函数y＝cosx，在教材中已研究了它们的定义域、值域、单调性、奇偶性、周期性．除了上述有关内容之外，有关正弦函数、余弦函数等对称性问题在高考中经常出现，有必要对其做进一步的探讨．函数y＝sinx，x∈R的图象是中心对称图形，并且有无穷多个对称中心，对称中心是图象与x轴的任一交点，坐标为(kπ，0)(k∈Z)；函数y＝cosx，x∈R的对称中心坐标为(kπ＋π2，0)(k∈Z)，以上两个函数图象，也是轴对称图形，它们的对称轴分别是x＝kπ＋π2(k∈Z)和x＝kπ(k∈Z)；函数y＝tanx的对称中心坐标为(kπ2，0)(k∈Z)，但它不是轴对称图形．正弦函数y＝sinx，余弦函数y＝cosx，在教材中已研究了它们的定义域、值域、单调性、奇偶性、周期性．除了上述有关内容之外，有关正弦函数、余弦函数等对称性问题在高考中经常出现，有必要对其做进一步的探讨．函数y＝sinx，x∈R的图象是中心对称图形，并且有无穷多个对称中心，对称中心是图象与x轴的任一交点，坐标为(kπ，0)(k∈Z)；函数y＝cosx，x∈R的对称中心坐标为(kπ＋π2，0)(k∈Z)，以上两个函数图象，也是轴对称图形，它们的对称轴分别是x＝kπ＋π2(k∈Z)和x＝kπ(k∈Z)；函数y＝tanx的对称中心坐标为(kπ2，0)(k∈Z)，但它不是轴对称图形．第一章三角函数典例5求函数y＝sin(2x－π6)的对称中心和对称轴方程．[思路分析]利用三角函数的图象，把2x－π6看作一个变量，用换元的方法求对称中心或对称轴方程，也可以考虑y＝sinx与y＝sin(2x－π6)的关系，利用变换的思想求对称轴与对称中心．求函数y＝sin(2x－π6)的对称中心和对称轴方程．[思路分析]利用三角函数的图象，把2x－π6看作一个变量，用换元的方法求对称中心或对称轴方程，也可以考虑y＝sinx与y＝sin(2x－π6)的关系，利用变换的思想求对称轴与对称中心．第一章三角函数[解析]设A＝2x－π6，则函数y＝sinA的对称中心为(kπ，0)，即2x－π6＝kπ，x＝kπ2＋π12，k∈Z，对称轴方程为2x－π6＝π2＋kπ，x＝π3＋k2π，k∈Z.所以y＝sin(2x－π6)的对称中心为(kπ2＋π12，0)，k∈Z，对称轴为x＝π3＋k2π(k∈Z)．『规律总结』本例中给出求三角函数的对称轴与对称中心的两种方法，这都是解决三角问题的基本方法，要切实理解好．[解析]设A＝2x－π6，则函数y＝sinA的对称中心为(kπ，0)，即2x－π6＝kπ，x＝kπ2＋π12，k∈Z，对称轴方程为2x－π6＝π2＋kπ，x＝π3＋k2π，k∈Z.所以y＝sin(2x－π6)的对称中心为(kπ2＋π12，0)，k∈Z，对称轴为x＝π3＋k2π(k∈Z)．感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明谢谢观看新课标导学数学必修④·人教A版