第九章面板数据模型,动态面板数据模型

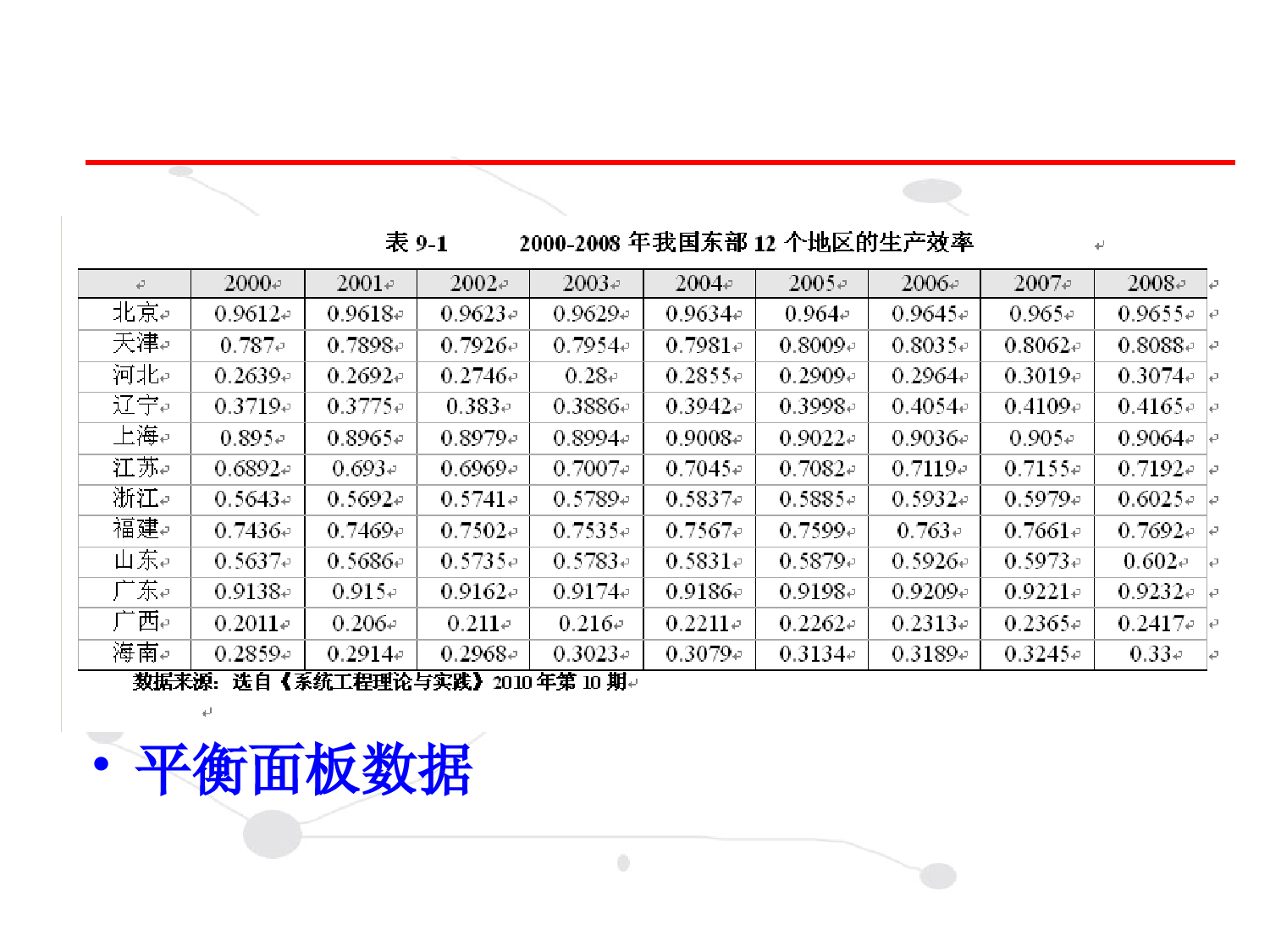
第九章面板数据模型第一节面板数据第二节面板数据回归模型第三节混合回归模型第四节变截距回归模型第五节变系数回归模型第六节效应检验与模型形式设定检验第七节面板数据的单位根检验和协整检验第八节案例分析面板数据（PanelData）：也叫平行数据，指某一变量关于时间和横截面两个维度的数据，记为xit，其中，表示N个不同的对象（如国家、省、县、行业、企业、个人）,，表示T个观测期。12,,,iN12,,tT第一节面板数据•平衡面板数据•非平衡面板数据•扩展的面板模型1.伪面板模型：如果按照某种属性(例如，年龄、职业和身份等)将各期调查对象分成不同的群；对于各个观测期，选择各群内观测数据的均值(中位数或分位数)，即可构造以群为‘个体’单位的面板数据。我们把这种以群为个体而构造的人工面板数据为伪面板数据(PseudoPanelData)。2.轮换面板模型:同一个个体可能不愿被一次又一次的被回访，为了保持调查中个体数目相同，在第二期调查中退出的部分个体，被相同数目的新的个体所替代，这种允许研究者检验“抽样时间”偏倚效应（初次采访和随后的采访之间的回答有显著的改变）的存在性叫轮换面板。对于轮换面板，每批加到面板的新个体组提供了检验抽样时间偏倚效应的方法。3.空间面板模型:当考虑国家、地区、州、县等相关截面数据时，这些总量个体可能表现出必须处理的截面相关性。现在有大量运用空间数据的文献处理这种相关性。这种空间相依模型在区域科学和城市经济学中比较普遍。具体来说，这些模型使用经济距离测度设定了面板数据的空间自相关性和空间结构（空间异质性）。4.计数面板模型:被解释变量是计数面板数据的例子很多。例如，一段时间内一家公司的竟标次数、一个人去看医生的次数、每天吸烟者的数量及一个研发机构登记专利的数目。虽然可以运用传统面板回归模型对计数面板数据建模，但鉴于被解释变量具有0及非负离散取值的特征，运用泊松面板回归模型建模更为合适。第二节面板数据回归模型一、面板数据回归模型的一般形式：其中，i=1,2,…,N表示个N个体；t=1,2,…,T表示T个时期；yit为被解释变量,表示第i个个体在t时期的观测值；xkit是解释变量,表示第k个解释变量对于个体i在时期t的观测值；是待估参数；uit是随机干扰项。ittiitKkitkitkitituuxy,10kit称为个体效应。反映个体不随时间变化的差异性。称为时间效应。反映不随个体变化的时间上的差异性。ittiitKkitkitkitituuxy,10it在上式模型中，样本容量（NT）远远小于参数个数，这使得模型无法估计。为了实现模型的估计，可以分别建立以下两类模型：从个体成员角度考虑，建立含有建立含有NN个个体个个体成员方程的成员方程的PanelDataPanelData模型模型；在时间点上截面，建立含有建立含有TT个时间点截面方程的个时间点截面方程的PanelDataPanelData模模型型。ittiitKkitkitkitituuxy,1011．含有．含有NN个个体成员方程的个个体成员方程的PanelDataPanelData模型模型PanelData模型简化为如下形式：ittiitKkitkitkiituuxy,1022．含有．含有TT个时间截面方程的个时间截面方程的PanelDataPanelData模型模型PanelData模型简化为如下形式：ittiitKkitkitktituuxy,10ittiitKkitkitkitituuxy,10二、面板数据回归模型的分类由于含有N个个体成员方程的式和含有T个时间截面方程的式两种形式的模型在估计方法上类似，因此本章主要讨论含有N个个体成员方程的PanelData模型的估计方法。根据对截距项和解释变量系数的不同假设，可将面板数据回归模型分为：混合回归模型、变截距回归模型和变系数回归模型3种类型。ittiitKkitkitkiituuxy,10混合回归模型:假设截距项和解释变量系数对于所有的截面个体成员都是相同的，即假设在个体成员上既无个体效应，也无结构变化。ittiitKkitkitkiituuxy,10混合回归模型的模型形式为:ititKkitkitkituxy,10TtNi,2,1,,2,1变截距回归模型:假定在截面个体成员上截距项不同，而模型的解释变量系数是相同的ittiitKkitkitkiituuxy,10变截距回归模型的模型形式为:ittiitKkitkitkituuxy,10变系数回归模型:假定在截面个体成员上截距项和模型的解释变量系数都不同。ittiitKkitkitkiituuxy,10根据和与模型解释变量是否相关，面板数据的个体效应和时间效应又分两种情形：固定效应和随机效应。ittiitKkitkitkiituuxy,10如果个体效应与模型中的解释变量是相关的,我们就称这种个体效应是固定效应。反之，如果个体效应与模型中的解释变量是不相关的，我们称之为随机效应。itii如果时间效应与模型中的解释变量是相关的,我们就称这种时间效应是固定效应。反之，如果时间效应与模型中的解释变量是不相关的，我们称之为随机效应。tt第三节混合回归模型从时间上看，不同年份之间不存在显著性差异；从截面上看，不同个体之间也不存在显著性差异，那么就可以直接把面板数据混合在一起(相当于将多个时期的截面数据放在一起作为样本数据)，用普通最小二乘法（OLS）估计参数，且估计量是线性、无偏、有效和一致的。一、混合回归模型二、混合回归模型的估计（Eviews操作）第四节变截距回归模型一、变截距模型的分类讨论三种类型，即个体固定效应变截距模型、时点固定效应变截距模型、时点个体固定效应变截距模型。ittiitKkitkitkituuxy,10变截距模型ittiitKkitkitkiituuxy,10（一）固定效应变截距模型1.个体固定效应变截距模型一般形式：其中，表示不同个体之间的差异化效应。itiitKkitkitkituuxy,10i2.时点固定效应变截距模型一般形式：其中，表示不同截面（时点）之间的差异化效应。ittitKkitkitkituuxy,10t3.时点个体固定效应变截距模型一般形式：ittiitKkitkitkituuxy,10ittiitKkitkitkituuxy,10（二）随机效应变截距模型讨论三种类型，即个体随机效应变截距模型、时点随机效应变截距模型、时点个体随机效应变截距模型。ittiitKkitkitkituuxy,10面板数据模型中的参数估计量既不同于截面数据估计量，也不同于时间序列估计量，其估计方法随着模型形式变化而变化。（一）固定效应变截距模型的估计1.最小二乘虚拟变量（LSDV）估计二、变截距模型的估计（1）个体固定效应变截距模型一般形式：itiitKkitkitkituuxy,10（2）时点固定效应变截距模型一般形式：ittitKkitkitkituuxy,10（3）时点个体固定效应变截距模型一般形式：ittiitKkitkitkituuxy,10(1)(1)截面加权(个体截面异方差情形的GLS估计计)2.2.广义最小二乘估计个体截面异方差是指各个个体方程的随机干扰项之间存在异方差，但个体和时期之间协方差为零。当残差具有个体截面异方差时最好进行截面加权回归：(2)(2)同期相关协方差情形的同期相关协方差情形的SURSUR估计估计同期相关协方差是指不同的个体成员同一时期的随同期相关协方差是指不同的个体成员同一时期的随机干扰项是相关的，但其在不同时期之间是不相关机干扰项是相关的，但其在不同时期之间是不相关的。的。当残差具有同期相关协方差情形时，SUR加权最小二乘是可行的GLS估计量：此时的SUR估计为：（二）随机效应变截距模型的估计EViews按下列步骤估计随机影响模型：第五节变系数回归模型前面所介绍的变截距模型中，横截面成员的个体影响是用变化的截距来反映的，即用变化的截距来反映模型中忽略的反映个体差异的变量的影响。然而现实中变化的经济结构或不同的社会经济背景等因素有时会导致反映经济结构的参数随着横截面个体的变化而变化。因此，当现实数据不支持变截距模型时，便需要考虑这种系数随横截面个体的变化而改变的变系数模型。变系数模型的一般形式如下：ittiitKkitkitkiituuxy,10为变系数，反映模型结构随截面的变化而变化。ki类似于变截距模型，变系数模型也分为固定影响变系数模型和随机影响变系数模型两种类型。EViews按下列步骤估计变系数模型：第六节效应检验与模型形式设定检验一、Hausman检验建立面板数据模型前的首要任务是确定被解释变量与截距项和系数的关系，截距项是否相同、系数是否一致，是固定效应还是随机效应模型，从而避免模型设定的偏差，改进参数估计的有效性。对于如何检验模型中个体效应或时间效应与解释变量之间是否相关，Hausman（1978）提出了一种严格的统计检验方法——Hausman检验。固定效应模型：LSDV估计量无偏；GLS估计量有偏。随机效应模型：LSDV和GLS估计量都无偏，但LSDV估计量有较大方差；。固定效应模型：LSDV估计量和GLS估计量的估计结果有较大的差异。Hausman检验的原理Hausman证明在原假设下，统计量W服从自由度为k（模型中解释变量的个数）的分布，即Step1：设定原假设H0:模型的个体效应或时间效应与解释变量无关；Step2：构造Hausman检验的W统计量Hausman检验其中b，分别为回归系数的LSDV估计向量，GLS估计向量；为之差的方差，即]ˆ[ˆ]ˆ[1bbWˆˆ]ˆ[ˆbVarˆb、2)(~]ˆ[ˆ]ˆ[21kbbWHausmanHausman检验的操作检验的操作EViews中可以实现检验模型中个体影响与解释变量之间是否相关的Hausman检验。为了实现Hausman检验，必须首先估计一个随机效应模型。然后，选择View/Fixed/RandomEffectsTesting/CorrelatedRandomEffects-HausmanTest，EViews将自动估计相应的固定效应模型，计算检验统计量，显示检验结果和辅助回归结果。二、模型形式设定检验模型形式设定检验为了检验面板数据模型的类型：混合回归模型、变截距回归模型还是变系数回归模型，经常使用的检验是协方差分析检验(F检验)，主要检验如下两个假设：H1：变截距回归模型H2：混合回归模型可见如果接受假设H2则可以认为模型为混合回归模型，无需进行进一步的检验。如果拒绝假设H2，则需检验假设H1。如果接受H1，则认为模型为变截距回归模型，反之拒绝H1，则认为模型为变系变系数数回归模型模型。下面介绍假设检验的F统计量的计算方法。首先计算变系数变系数回归模型模型的残差平方和，记为S1；变截距变截距回归模型模型的残差平方和记为S2；混合回归模型的残差平方和记为S3。)]1(),1)(1[(~))1(()]1)(1/[()(1132kTNkNFkNNTSkNSSF构造并计算统计量)]1(,)1[(~))1((])1/[()(1121kTNkNFkNNTSkNSSF例9-3第七节面板数据的单位根检验和协整检验一、面板数据的单位根检验（一）面板数据的单位根检验分类（二）面板数据的单位根检验应用举例二、面板数据的协整检验（一）检验方法分类（二）面板数据协整检验的应用举例一般情况下可以将面板数据的单位根检验划分为两大类：一类为相同根情形下的单位根检验，检验方法包括LLC（Levin-Lin-Chu）检验、Breitung检验；另一类为不同根情形下的单位根检验，检验方法包括Im-Pesaran-Skin检验、Fisher-ADF检验和Fisher-PP检验。一、面板数据的单位根检验（一）面板数据的单位根检验分类（二）面板数据的单位根检验应用举例面板数据的协整检验方法可以分为两大类，一类是建立在EngleandGranger二步法检验基础上的面板协整检验，具体方法主要有Pedroni检验和Kao检验；另一类是建立在Johansen协整检验基础上的面板协整检验。二、面板数据的协整检验（一）检验方法分类1、Pedroni检验Pedroni提出了基于EngleandGranger二步法的面板数据协整检验方法，该方法以协整方程的回归残差为基础构造7个统计量来检验面板变量之间的协整关系。2、Kao检验Kao检验和Pedroni检验遵循同样的方法，都是基于EngleandGranger二步法而发展起来的。但不同于Pedroni检验，Kao检验在第一阶段将回归方程设定为系数相同、截距项不同，第二阶段基于DF检验和ADF检验的原理，对第一阶段求得的残差序列进行平稳性检验。（二）面板数据协整检验的应用举例